Modifier un réseau carré de polygones, 4ieme partie(bis): Astuce de construction des facettes permettant de transformer Blender en grapheur 2D

Blender (jusqu'à 2.49)

Python:
créer un réseau carré de polygone.
4ieme partie (bis):
astuce de construction permettant de transformer
Blender en grapheur 2D.

Index Principal Index Python
PrécédentPython: automatiser...des facettes (4/5)	Python: lignes et colonnes differentes (5/6) Suivant

Attention : modification de l'API et de Blender
Fichier d'exemple pour Blender 2.42

Il ne s'agit ici que d'un a parte, sur la possibilité de ne traiter qu'un partie de la facette.
Lorque l'on modélise un réseau de polygone à la main, en utilisant les commandes habituelles:

1/ Créer un Mesh
2/ TAB pour passer en mode d'édition
3/ CTRL-bouton-gauche pour ajouter des points.

Le résultat de ce type de construction peut ressembler à :

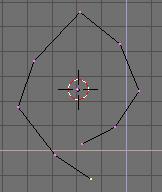
La question que l'on se pose est :

pouvons nous imiter cela à partir du langage de programmation?

Bien sûr, et il n'y a aucune difficulté. La réflexion que l'on mene pour arriver à trouver la solution est la suivante: Blender ne dessine que les bords des facettes, donc si je ne vois qu'une ligne, c'est qu'il s'agit d'une facette incomplète: il lui manque le troisième point pour former un triangle. C'est l'évidence même.

Décomposons les opérations:

1/ création du Mesh par l'appel à la méthode Blender.NMesh.GetRaw()

m=Blender.NMesh.GetRaw()

2/ Création d'une liste de points, ou sommets (quoiqu'ils ne deviendront vraiment des sommets que lorsqu'on les utilisera pour fabriquer les facettes)

Pour cela on se donne une limite et on utilise une boucle Range()

limite=n
for n in Range(limite):
      x=f(quelque chose pour x)
      y=f(quelque chose pour y)
      z=f(quelque chose pour z)
      vert=NMesh.Vert(x,y,z)
      m.verts.append(vert)

On crée le point et on le place dans la liste de vertices de m

...
      vert=NMesh.Vert(x,y,z)
      m.verts.append(vert)

0 1 2 3 4 5 etc.

3/ pour créer les faces il faudra prendre un sommet et son successeur dans la liste. Par exemple le verts[0] et le verts[1] formeront la première facette, verts[1] et le verts[2] la suivante etc. La boucle s'arrête sur l'avant dernier sommet pour qu'il n'y ait pas d'erreur, c'est-à-dire limite -1.

...
for n in range(limite-1):
    f=NMesh.Face()
    f.v.append(m.verts[n])
    f.v.append(m.verts[n+1])
    m.faces.append(f)

Attention : modification de l'API et de Blender

les versions récentes de Blender sont réglées pour contrôler le nombre de sommets par face et il n'est donc plus possible de créer des faces avec seulement deux sommets valides car la moindre surface suppose l'existance d'un triangle donc d'au moins 3 sommets . Une nouvelle notion a été indroduite : l'edge ou si on veut bien le considérer sous l'angle francophone le segment. Ces segments sont ajoutés au mesh comme une liste à part entière à la manière des faces et des sommets . Nouvelle formulation :

...
for n in range(limite-1):
m.addEdge(m.verts[n], m.verts[n+1])

Exemple concret:
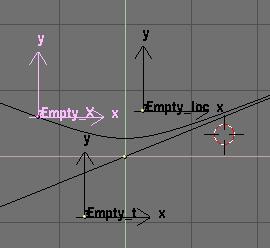
Dans cet exemple il s'agit de l'équation paramétrée de l'hyperbole. L'execution du script est lié au deux objets Empty_loc et Empty_t (la méthode de liaison sera peut-être l'objet d'un autre tutoriel). Lorsque Empty_t ou Empty_loc sont déplacés, l'affichage est modifié.

Téléchargez ce fichier Blend.
Téléchargez ce fichier Blend pour Blender 2.42 et suivants.
Téléchargez une variante avec des fonctions circulaires.

Le script python:

import Blender
from Blender import *
from Blender import NMesh

import math
from math import *

#le nombre limite de points que l'on veut
#voir apparaitre
limite=256

#le parametre t varie entre -1.0 et 1.0
PI2=1.999

#la quantite que l'on ajoute a t
prog=PI2/limite

#la position a l'instant t
X=Object.Get('Empty_X')

#valeur de la pente qui donne la courbure
T=Object.Get('Empty_loc')
a=T.LocX
b=T.LocY

t0=Object.Get('Empty_t')
t=t0.LocX

y=a*(1+t*t)/(1-t*t)
x=b*(2*t)/(1-t*t)

X.LocX=x
X.LocY=y

#le nouveau mesh
m=NMesh.GetRaw()

#le point de départ des calculs
tn=-0.99

#boucle de construction des sommets
for n in range(limite):
tn=tn+prog

yn=a*((1+tn*tn)/(1-tn*tn))
xn=b*((2*tn)/(1-tn*tn))

vert=NMesh.Vert(xn,yn,0)
m.verts.append(vert)

#boucle de construction des segments
#qui relient les sommets
for n in range(limite-1):
    f=NMesh.Face()
    f.v.append(m.verts[n])
    f.v.append(m.verts[n+1])
    m.faces.append(f)

NMesh.PutRaw(m,'corde')

PrécédentPython: automatiser...des facettes (4/5)	Python: lignes et colonnes differentes (5/6) Suivant
Vers le Haut de page

Les questions concernant cette page peuvent être posées sur :
news://news.zoo-logique.org/3D.Blender