 |
Standard Performance Evaluation Corporation |
   |
|
|
|
Defects in SFS 2.0 Which Affect the Working-Setby Stephen Gold, SFS vice-chair FINAL DRAFT, last updated 19 July 2001
1.0 Executive SummarySignificant defects have recently been discovered in the SFS 2.0 benchmark suite, causing it to be withdrawn. Each of these defects tends to reduce the size of the benchmark's working-set as the number of load-generating processes is reduced. Since test-sponsors have great freedom in deciding how many processes to use, the resulting variations in the working-set hamper meaningful comparison of SFS 2.0 test results. Defect #1 manifests when the requested ops/sec/process is in the hundreds. In observed incidents, the working-set of the benchmark may be reduced as much as 27%. Defect #2 manifests whenever the requested ops/sec/process is 26 or more. The working-set of the benchmark may be reduced by a factor of three or more. Defect #3 manifests only when the requested ops/sec/process is 500 or more. The working-set of the benchmark may be be reduced two orders of magnitude or more. Defect #4: Even if the first three defects were corrected, the cache profile of the working-set would still vary with the number of load-generating processes used. As processes are reduced, the fileset distribution narrows. Because of these defects, many of the published SFS 2.0 results are not comparable. Comparability exists only for results that were run on servers which would have cached the intended working-set of the benchmark. Based on simulation, it is believed that 115 out of the 248 approved SFS 2.0 results meet this criterion for comparability. 2.0 Technical BackgroundThe SFS 2.0 benchmark suite was released by SPEC December 1997. SFS 2.0 is used to evaluate and compare the performance of fileservers under steady NFS loads. SFS 2.0 was withdrawn by the SPEC Open Systems Group in June 2001 due to the defects which are the subject of this document. Important features of SFS 2.0 included:
The SFS 2.0 suite consists of two workloads, SPECsfs97.v2 and SPECsfs97.v3. The differences between the two workloads boil down to the operation-mixes used. Data-set generation, file selection, and rate regulation are done exactly the same way for both workloads. Thus, defects in these areas affect both workloads. Much of the remainder of this discussion assumes that the reader is a licensee with access to the source-code. But sufficient detail is presented to allow a non-licensee to grasp the broad outlines of how the benchmark works and what went wrong. 2.1 Working-SetThe working-set of an NFS workload over an interval is the number of distinct filesystem blocks accessed during the interval. All modern NFS servers have some ability to cache frequently-accessed filesystem blocks in their buffer cache for later reuse. This is done to reduce the probability that any particular access will require a (costly) disk read. On many servers, the buffer cache is smaller than the working-set of the SFS 2.0 benchmark over its 300-second measurement phase. (One reason for the 300-second warmup phase in SFS 2.0 is to warm up the cache sufficiently to approximate the steady-state behavior.) For such servers, changes to the working-set size can have a large impact on the number of disk operations, the utilization of the CPU and disks, achievable throughput, and average response-times. 2.2 How the SFS 2.0 dataset is GeneratedThe design intent of SFS 2.0 was that the dataset would be 10 MBytes per op/s of requested load. Looking at the implementation (sfs_c_chd.c) we see that each load-generating process has its own dataset, rooted in its own subdirectory, with no sharing between processes. The dataset of each process consists of four so-called "working sets". Each "working set" is used for a different group of NFS operations:
In this paper we are mainly concerned with the Io_working_set. The code that sizes the "working sets" is in sfs_c_man.c. Num_io_files gets set to roughly 390 times the requested op/sec for the process. The INIT phase ensures that this number of "I/O" files (with names like file_en.00001) get created on the server. Since the average file size is about 27 KBytes, this works out to about 10 MBytes per requested op/sec. Note that the acheived ops/sec reported in the benchmark disclosure generally differs slightly from the requested ops/sec. 2.3 How "I/O" Files are SelectedThe design intent of SFS 2.0 was that only 10% of the files would be accessed in the course of a run, and furthermore that the files would be accessed according to a Poisson distribution, causing some files to be accessed much more frequently than others. Num_working_io_files is set to roughly 10% of Num_io_files. The init_fileinfo() function in sfs_c_chd.c randomly selects Num_working_io_files of the "I/O" files to go into the Io_working_set. To facilitate generation of the Poisson distribution, the Io_working_set is divided into eight or more access-groups of roughly equal size. An access-group in the Io_working_set typically contains about 100 files. The number of access-groups is always a multiple of four. To be precise: group_cnt = 8 + ((Num_working_io_files/500) * 4) Each access-group is assigned a relative weight, called "next_value". The sum of the weights from 0 to i is stored in Io_working_set.entries[i].range. Then the sum of all the weights is stored in Io_working_set.max_range. When a load-generating process wants to generate an NFS operation, it calls the do_op() function in sfs_c_chd.c, which calls op(). If the operation chosen by do_op() is one which uses the Io_working_set, op() calls randfh() with file_type=Sfs_io_file. Some operations (like READ and WRITE) may call randfh() more than once, until they find a file with particular properties. In order to pick an access-group, randfh() generates a random value between 0 and (Io_working_set.max_range - 1), inclusive. It then does a binary search, starting at Io_working_set.max_range/2 - 1 and proceeding until it finds a group such that either:
or
If the random value were uniformly distributed and the ".range" fields were monotonically non-decreasing, the probability of selecting a particular group would be: (Io_working_set.entries[group].range - Io_working_set.entries[group - 1].range)/Io_working_set.max_range (if group > 1) or Io_working_set.entries[0].range/Io_working_set.max_range (if group = 0) which would equal next_value/Io_working_set.max_range . (Recall that a different next_value is computed for each group.) In order to pick a file, randfh() generates random offsets within the selected group. If the operation is a READ or a non-append WRITE, randfh() keeps generating offsets until it finds a file that is large enough for the current operation. 2.4 How Request Rates are RegulatedBetween calls to do_op(), the load-generating processes sleeps by calling msec_sleep(). Each load-generating process regulates its request rate independantly from the other processes. This is done by periodically adjusting the average sleep-time, Target_sleep_mspc. The goal of the adjustment is to find a value of Target_sleep_mspc which causes the process to generate its share of the requested total rate, which is Child_call_load. The same adjustment algorithm is used for both the warmup phase and the measurement phase, just with different parameters. It is fairly simple. A process starts the warmup phase with Target_sleep_mspc calculated based on sleeping 50% the time. After a period of time has elapsed, the process calls check_call_rate() to adjust Target_sleep_mspc. The check_call_rate() function begins by comparing actual requests generated since start of the current phase (Reqs_this_test) with a target based on multiplying the Child_call_load by elapsed time in the current phase (elapsed_time). The difference between the target and actual requests is added to the normal request count for the upcoming check-period (req_target_per_period) and that is the number of requests to be attempted in the upcoming check-period. In other words, the process attempts to be completely caught up by the end of the upcoming check-period. The check_call_rate() function sets Target_sleep_mspc to reflect the number of requests to be attempted, the duration of a check-period, and the expected work time per request in the upcoming check-period. Since the actual work times are not known, the code substitutes (as an approximation) the average work time for all requests so far in the current phase. During the warmup phase, each check-period lasts for two seconds. Since the warmup phase is 300 seconds, a total of 150 checks are made during the warmup phase. By that time the Target_sleep_mspc has hopefully converged to a stable value. During the measurement phase (which lasts for another 300 seconds) the checking and adjustments continue, but the check-period is increased to 10 seconds. The load-generating process does not attempt to sleep for exactly Target_sleep_msec each time. Instead, it generates a random number of milliseconds (rand_sleep_msec) which is distributed uniformly between roughly 50% and 150% of Target_sleep_msec. This randomized sleep interval is passed to msec_sleep(), which in turn calls the library function select(). The timeout argument passed to select is based directly on rand_sleep_msec. 3.0 Description of the Defects3.1 Defect #1: request-rate regulation is unstable, causing processes to sleep for many seconds, aka "The oscillation defect"discovered May 7, 2001 The rate adjustment algorithm described in Section 2.3 is highly aggressive. For instance, if the process generates twice the requested rate during first check-period of the warmup phase, it will try to recover completely during the second check-period. To do so, it will attempt to make zero requests during that period. This is rather extreme considering that there are still 149 periods remaining during the warmup phase! Because the adjustment algorithm is so aggressive, it tends to be unstable, particularly when the process is asked to generate a large number of requests per second. The instability of the adjustment algorithm is exacerbated by difficulties in accurately controlling the interval between requests. On many UNIX systems, the select() timeout resolution is one clock-tick, which typically means 10 msec. For instance, msec_sleep(1) is likely to sleep for at least 10 msec, for an error of >900% with respect to the requested interval! If the adjustment algorithm sees that the process is falling behind with Target_sleep_mspc=1, it is likely to try Target_sleep_mspc=0. This causes a sudden jump in the request-rate, lasting for an entire period. This can put the process so far ahead that it will stall for the period after that. Furthermore, SFS 2.0 tests are usually run with more load-generating processes than CPUs. This means that processes whose select() timeout has expired may have to wait for another process to relinquish the CPU before it can return from select() and generate another request. This increases the upredictability of the msec_sleep() function and tends to introduce further instability. The instability, when present, can be observed by enabling the CHILD_XPOINT debugging code in check_call_rate(), which can be accomplished by setting DEBUG=6 in the sfs_rc file. If you see debug output containing the string " 0 call, rqnd " then you will know that one of the load-generating processes generated zero calls for that check-period. The zero-call behavior has been observed both during warmup phases and measurement phases. With respect to measurement phases, the behavior has been observed for request-rates ranging from 200 to 400 ops/sec/process, affecting 6-27% of the adjustment periods. It is possible that the defect could occur for request-rates outside-this range. When a load-generating process experiences a zero-call period during the measurement phase, its portion of the fileset receives no accesses for ten seconds. Over that interval, the working-set of the benchmark is reduced by 1/N from the intended working-set, where N is the total number of load-generating processes. Smaller oscillations in the request-rate, say from 50% to 150% of the requested rate, would also tend to reduce the working-set, though the effect is harder to quantify. To summarize:When the requested ops/sec/process is in the hundreds, instability in the rate regulation algorithm can cause the request-rate of a process to oscillate wildly. Sometimes the request-rate of a process goes to zero for ten seconds at a time. The frequency and severity of the problem are poorly understood. In observed incidents, the working-set of the benchmark was reduced by 6%-27%. 3.2 Defect #2: I/O access-group probabilities can round to zero, aka "The distribution defect"discovered May 7, 2001 The next_value variable (i.e., the weight given to access-group i) is calculated as: next_value = (int) (1000 * (cumulative_lambda_power /
(e_to_the_lambda * cumulative_x_factorial)))
where:
and
Whenever the requested ops/sec/process is in the range 26 to 38, there will be 16 access groups, lambda = 8, and e_to_the_lambda = 2980.96. This causes access-group #0 to have next_value of: (int) (1000 * (1.0 / (2980.96 * 1.0)))) = (int)0.335 = 0 So Io_working_set.entries[0].range == 0, which mean that group #0, containing roughly 6% of the Io_working_set files is never selected by randfh(Sfs_io_file). In effect, the probability of access, which should have been 0.03%, got rounded down to zero. As the request-rates increase, so do group_cnt, lambda, and e_to_the_lambda. next_value=0 occurs for more and more access-groups, making them inaccessible. This phenomenon starts at the margins of the distribution (groups 0 and group_cnt-1, where the Poisson probabilities are lowest) and spreads inward toward the mode, as illustrated in the following table: Requested Number of I/O access-groups: Inaccessible
ops/proc total inaccessible accessible I/O access-groups:
1-12 8 0 (0%) 8 none
13-25 12 0 (0%) 12 none
26-38 16 1 (6%) 15 {0}
39-51 20 2 (10%) 18 {0-1}
52-64 24 3 (13%) 21 {0-2}
65-76 28 5 (18%) 23 {0-3, 27}
77-89 32 8 (25%) 24 {0-5, 30-31}
90-102 36 11 (31%) 25 {0-6, 32-35}
103-115 40 13 (33%) 27 {0-7, 35-39}
116-128 44 17 (39%) 27 {0-9, 37-43}
129-141 48 19 (40%) 29 {0-10, 40-47}
142-153 52 22 (42%) 30 {0-11, 42-51}
...
193-205 68 35 (51%) 33 {0-18, 52-67}
...
295-307 100 60 (60%) 40 {0-30, 71-99}
...
398-410 132 87 (66%) 45 {0-44, 90-131}
411-423 136 90 (66%) 46 {0-45, 92-135}
424-435 140 93 (66%) 47 {0-47, 95-139}
436-448 144 97 (67%) 47 {0-49, 97-143}
...
475-487 156 107 (69%) 49 {0-54, 104-155}
488-499 160 111 (69%) 49 {0-56, 106-159}
The "inaccessible" groups in this table are just the ones which have next_value=0. Here is the same data presented in graphical form: 
Note that below 26 requested ops/sec/proc, all the access-groups are accessible and this defect has no effect. The trend would continue past 500 requested ops/sec/proc, except that at that point the existence of defect #3 complicates the issue. Inaccessible I/O access-groups reduce the number of files accessed from what the benchmark intended. Of the "Files accessed for I/O operations" printed in the client log, it might be the case that only 1/3 were truly accessible via those operations. Thus the I/O operations get concentrated over a smaller set of files than was intended. The inaccessible files are precisely the ones that would be accessed least frequently in a correct Poission distribution. On the other hand, these files are also the ones that are most likely to miss in the server's buffer cache, so their inaccessibility could have a relatively large impact on buffer-cache miss-rates. Buffer-cache miss-rates could affect the average response-times reported by the benchmark as well as the peak throughputs. Don Capps of Hewlett-Packard has created a simulation of the SFS 2.0 benchmark which can quickly determine, for a given SFS 2.0 result, what fraction of the Io_working_set access-groups were inaccessible due to this defect. To summarize:Whenever the requested ops/sec/process is 26 or more, there are some I/O access-groups which cannot be accessed because their probability of access is zero. The number of inaccessible access-groups generally increases as the request-rate increases. At 475 requested ops/sec/process, the working-set of the "I/O operations" in SFS 2.0 is reduced by more than a factor of three. 3.3 Defect #3: I/O access-group ranges can be negative, aka "The floating-point overflow defect"discovered May 7, 2001 Recall that the next_value (the weight of access-group i) is calculated as: next_value = (int) (1000 * (cumulative_lambda_power /
(e_to_the_lambda * cumulative_x_factorial)))
All three variables in the right-hand side of the assignment are double-precision. If the load-generating client implements IEEE Standard 754 floating point (as most do) the largest accurately-represented value is roughly 2e+308. For 500 requested ops/sec/process, there are 164 groups and lambda=82. Something strange happens for group #162, since cumulative_lambda_power (82 to the 162nd power) is roughly 1e+310, which is represented as Infinity. The denominator is also Infinity, since e_to_the_lambda (4.094e+35) times cumulative_x_factorial (1.22969e+289) also overflows 2e+308. So the quotient is Infinity divided by Infinity, or NaN (not-a-number). 1000 times NaN is still NaN. And converting NaN to an int results in (2^31 - 1) or 2147483647. Now, the "range" values for each access-group are declared as ints. It so happens that previous_range = Io_working_set.entries[161].range = 970. Adding 2147483647 and 970 using 32-bit twos-complement arithmetic (which is what most compilers generate for ints) yields -2147482679, which is stored in Io_working_set.entries[162].range. Since the NaN also occurs for i=163, next_value is (2^31 - 1) again. Io_working_set.entries[163].range and Io_working_set.max_range both get set to 968. Now one of the assumptions of the binary search algorithm (namely, that the "range" fields are monotonically non-decreasing) has been violated for the last two access-groups. This violation is the basis for defect #3. For 164 groups this defect is not a serious matter, since the binary search starts at group=81 and never reaches the last two access-groups for any random value between 0 and 967. As the request-rate increases beyond 512 requested ops/sec/process, so do group_cnt, lambda, and e_to_the_lambda. next_value=NaN occurs for more and more access-groups. As long as the NaNs are confined the highest access-groups and there are an even number of NaNs, this defect has little or no effect. However, if the number of NaNs happens to be odd instead of even (as happens when there are 168 or 176 groups) then Io_working_set.max_range will be a large negative integer. In this case the random value generated will be a positive number in the range 0 to 1-max_range. The effect is to cause the vast majority of accesses to go to one or two access-groups. For example, consider a process with 168 access-groups. There are seven NaNs and max_range = -2147482689. The binary search algorithm picks a value in the range 0 to 2147482690. The binary search algorithm starts at group=83, which has Io_working_set.entries[83].range = 469. By far the most likely scenario is that the random value is greater than 966, in which case the binary search examines groups 125, 146, 157, 162, 165, and 166, before settling on group=167. Over the course of a 300-second measurement phase (in which the process generates on the order of a million I/O operations) the expected number of random values between 0 and 966 is less than 1. In effect, the working-set for I/O operations has been reduced to a single access-group. For exactly 304 access-groups, max_range is zero, causing a division by zero error which terminates the benchmark with a core dump. When the number of access-groups exceeds 304, the NaNs invade the middle access-groups, where the binary search starts. Even if the number of NaNs is even, the binary search algorithm can get seriously confused by them. Once again, the effect is to cause the vast majority of accesses to go to one or two access-groups. For example, consider a process with 324 access-groups. This time there are 184 NaNs and max_range=-162. The binary search algorithm picks a value in the range 0 to 161. The binary search algorithm starts at group=161. But: Io_working_set.entries[161].range = 0 and Io_working_set.entries[162].range = 2147483647. By walking through the code, you can see that group #161 is selected for value=0 and group #162 is selected for 0 < value < 162: if (work_set->entries[group].range == value)
break;
if (work_set->entries[group].range > value) {
...
} else if (work_set->entries[group].range < value) {
if (work_set->entries[group+1].range > value) {
group++;
break;
Thus, out of 324 groups, only two groups are accessible, and group #162 gets over 99% of the I/O accesses. Don Capp's simulator calculates the group-access probabilities, generates random numbers, and performs the binary search using algorithms equivalent to those in the SFS 2.0 load generator. The number of accesses simulated is always 300 times the requested ops/sec. This is slightly unrealistic because (for various reasons) the actual number of I/O accesses per requested op is not really unity. Nevertheless the simulator provides a very convincing illustration of how the number of I/O access-groups actually accessed varies for different numbers of requested ops/sec/process. The following table, generated using the simulator, shows how the number of groups with next_value=0 and next_value=NaN varies for selected numbers of access-groups. The last column shows how many access-groups were actually selected by the binary search algorithm after it had been invoked millions of times. Requested number of I/O access-groups: ops/proc total next_value=0 next_value=NaN selected via binary search 488-499 160 111 0 49 (31%) 500-512 164 112 2 49 (30%) 513-525 168 111 7 2 (1%) 526-538 172 109 12 46 (27%) 539-551 176 108 17 2 (1%) 552-564 180 106 22 45 (25%) ... 590-602 192 103 36 44 (23%) ... 629-641 204 99 50 44 (22%) ... 667-679 216 96 56 30 (14%) 680-692 220 96 68 30 (14%) 693-705 224 94 73 2 (<1%) 706-717 228 93 78 32 (14%) 718-730 232 92 82 33 (14%) ... 757-769 244 95 96 32 (13%) 770-782 248 96 100 32 (13%) ... 795-807 256 100 109 3 (1%) ... 885-897 284 113 140 28 (10%) 898-910 288 113 145 1 (<1%) 911-923 292 116 149 1 (<1%) 924-935 296 118 153 1 (<1%) 936-948 300 120 158 1 (<1%) 949-961 304 122 162 [core-dump] 962-974 308 122 167 1 (<1%) 975-987 312 125 171 1 (<1%) 988-999 316 127 175 1 (<1%) 1000-1012 320 129 180 2 (<1%) 1013-1025 324 131 184 2 (<1%) 1026-1038 328 133 188 1 (<1%) Here is the same data presented in graphical form: 
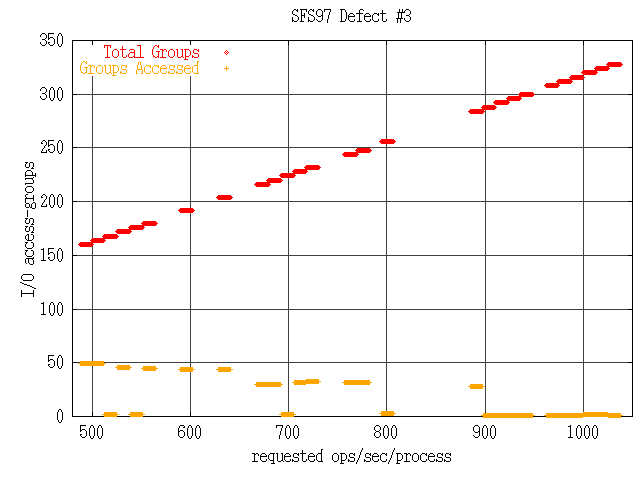
To summarize:NaNs are generated whenever the requested ops/sec/process is 500 or more. These NaNs cause violation of the assumptions underlying the algorithm used to select access-groups. When the number of NaNs is even and less than 150, the number of groups accessed generally declines as the request-rate increases, reaching 28 groups at 897 requested ops/sec/process. The working-set of the "I/O operations" in SFS 2.0 is reduced by up to an order of magnitude. When the number of NaNs is odd and/or greater than 150, the number of groups accessed is usually three or less, with most of the accesses going to a single group. The working-set of the "I/O operations" in SFS 2.0 is reduced by at least two orders of magnitude. 3.4 Defect #4: fileset distribution narrows as processes are reduceddiscovered June 5, 2001 Defects #2 and #3 can be remedied by making minor changes to the software which sets up the ranges. But even if the Poisson distribution were implemented as intended, there would still be a serious problem with the benchmark. The problem lies in the way the Poisson parameter "lambda" varies with the per-process request rate. Although buffer cache algorithms vary in detail from server to server, it is reasonable to assume that the cacheability of an access-group increases with its frequency of access. So when analyzing cache behavior, it makes sense to sort the access-groups in order of probability, so that the rank of the most frequently-accessed group is 1 and the rank of the least frequently-accessed group is N. Plotting a group's probability of access against its sorted rank produces a "cache profile" of the workload. As the number of groups grows, the cache profile becomes more and more concentrated on the left edge of the graph. In other words, a greater and greater fraction of the accesses occur in the busiest parts of the fileset. 
For a simple illustration, imagine a server which always hits in the most-frequently accessed 1/8 of the groups and always misses in the remaining 7/8 of the groups. For a target load is 50,000 ops/sec, the Io_working_set size is always roughly 50 GBytes. By simply varying the number of load-generating processes, the fraction of accesses which are to cached groups can be varied from 20% to 84%, as shown below: Procs Ops/proc Groups/proc Cached_Groups Lambda % cached 5000 10 8 5000 4 20.6% 1500 33 16 3000 8 28.1% 625 80 32 2500 16 38.5% 263 190 64 2104 32 52.1% 128 390 128 2048 64 68.3% 62 806 256 1859 128 84.2% The only constraints on the number of load-generating processes come from the performance capabilities of the server-under-test and compliance with the Uniform Access Rule (UAR). Of course, if the server-under-test caches the benchmark's working-set over the entire measurement phase, then the changes in the cache profile should have little or no impact on the results. To summarize:Even if the other three defects were corrected, the cacheability of the working-set would still vary with the number of load-generating processes used. This variability would invalidate any comparison of SFS 2.0 results for servers that were tested with different number of processes, unless it could be shown that both servers were operating entirely out of cache. 4.0 Effect on Approved ResultsA total of 248 SFS 2.0 results have been approved by SPEC. 247 of those results have been published on the SPEC website. (The remaining result is awaiting the vendor's decision whether or not to publish.) Don Capps's simulator has been used to demonstrate that 115 of the published SFS 2.0 results would have fit in the servers' memory even if the intended working-set had been achieved. Since the defects described in this report affect only the working-set of the benchmark, such results can be considered comparable to one another. Summarized simulation results for all 248 approved SFS 2.0 results are presented in Appendix A. Of the 248 approved results, the requested ops/sec/process at peak ranges from 18.89 to 1000. Only one result exceeded the 499 requested ops/sec/process threshold for triggering defect #3. 230 results (93%) exceeded the 25 requested ops/sec/process threshold for triggering defect #2. Because defect #1 has not been adequately modeled, it is unknown how many of the approved results might have triggered that defect. Of all the approved SFS 2.0 results, the five with the highest requested ops/sec/process at the peak were:
All five of these results were submitted in 2001. Aside from these five results, no other approved results exceeded 400 requested ops/sec/process. Using the tables in this report, one can see that:
According to the simulator, none of these five results was obtained with a server that could operate entirely out of cache with the intended working-set. So in each case the performance of the server-under-test was exaggerated by the defects described in this report. Many other results were affected as well. See Appendix A for more information about specific results. 5.0 ConclusionsSubstantial defects have recently been discovered in the SFS 2.0 benchmark suite, causing it to be withdrawn. Each of these defects tends to reduce the size of the benchmark's working-set as the number of load-generating processes is reduced. Since test-sponsors have great freedom in deciding how many processes to use, the resulting variations in the working-set hamper meaningful comparison of SFS 2.0 test results for servers that do not cache the entire dataset. Defect #1 manifests when the requested ops/sec/process is in the hundreds. Instability in the rate regulation algorithm can cause the request-rate of a process to go to zero for ten seconds at a time. The frequency and severity of the problem are poorly understood. In observed incidents, the working-set of the benchmark was reduced by 6%-27%. Defect #2 manifests whenever the requested ops/sec/process is 26 or more. Some I/O access-groups become inaccessible because their probability of access is rounded down to zero. The number of inaccessible access-groups generally increases as the request-rate increases. At 475 requested ops/sec/process, the working-set of the "I/O operations" in SFS 2.0 is reduced by more than a factor of three. About 92% of the approved SFS 2.0 runs suffered from inaccessible access-groups because of this defect, though in about half of those cases the reported performance is thought to have been unaffected because the server-under-test could hold the intended working-set in cache. Defect #3 manifests only when the requested ops/sec/process is 500 or more. Some I/O access-groups become inaccessible because propagation of floating-point overflows into NaNs result in violation of an assumption underlying the access-group selection algorithm. When the number of NaNs is even and less than 150, the working-set of the "I/O operations" in SFS 2.0 is reduced by up to an order of magnitude. When the number of NaNs is odd and/or greater than 150, the defect becomes much more serious and the working-set of the "I/O operations" in SFS 2.0 is reduced at least two orders of magnitude. Only one approved SFS 2.0 result has been affected by this defect. As of the publication of this report, that result has not been published on the SPEC website. Even if the first three defects were corrected, the cache profile of the working-set would still vary with the number of load-generating processes used. This variability would invalidate any comparison of SFS 2.0 results for servers that were tested with different number of processes, unless it could be shown that both servers were operating entirely out of cache. Because of these defects, many of the published SFS 2.0 results are not comparable. Comparability exists only for results that were run on servers which would have cached the intended working-set of the benchmark. Based on simulation, it is believed that 115 out of the 248 approved SFS 2.0 results meet this criterion for comparability. Appendix A: Simulation ResultsHere are the summarized simulation results for all 248 approved SFS 2.0 results. There are a few caveats to be considered in interpreting these results:
Here are the 98 approved SPECsfs97.v2 results, sorted by achieved throughput at peak:
Here are the 150 approved SPECsfs97.v3 results, sorted by achieved throughput at peak:
Home - Contact - Site Map - Privacy - About SPEC
webmaster@spec.org 
Last updated: Fri Sep 26 15:32:43 EDT 2003 Copyright 1995 - 2024 Standard Performance Evaluation Corporation URL: http://www.spec.org/sfs97/sfs97_defects.html |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||