Compositing Microformats

Editor: Toby Inkster

Authors: Toby Inkster, ... (contributors welcome)

This page is intended to explore compositing of microformats. What do composited microformats mean? What opportunities are there? Are there any problems in this area that need solving? If so, what should those solutions be?

The issue

Sometimes microformats are marked up like this:

<div class="hfoo hbar">...</div>

What does this mean?

• Possible meaning 1: Sometimes the author means "I'm describing something which is both an hfoo and an hbar simultaneously." For example, it's reasonable for something to be both a tagged link (xFolk) and a review (hReview) simultaneously. Properties of one (e.g. reviewer) can be reasonably assumed to apply to the other.
• Possible meaning 2: Sometimes an author means "I'm describing two different things, an hfoo and an hbar. They are attached to the same element merely for convenience." For example, if <div class="vcard vevent">...</div> is used, it is likely that the author just means to intermingle information about a person and an event — they are probably not trying to describe a "thing" which is both a person and an event simultaneously.

Nesting vs Compositing

Nesting is not compositing.

• Nesting: <div class="hfoo">...<p class="hbar">...</p>...</div>
• Compositing: <div class="hfoo hbar">...</div>

Ideas

• Are there some microformats which when composited always mean meaning 1? e.g. xfolkentry+hreview
  • Could we put together a list of these combinations?
• Are there some which always mean meaning 2? vcard+vevent seems likely.
  • Could we put together a list of these combinations?

Possible Answers

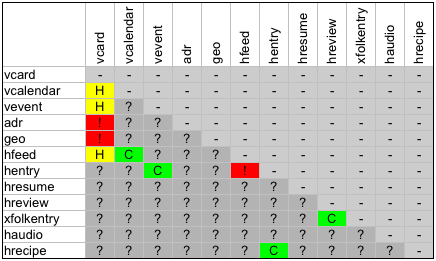
• C = Semantic composite (meaning #1 above)
• H = HTML composite (meaning #2 above)
• ! = Too confusing/ambiguous — do not use
• ? = What do you think?

Logic

Logical properties of the "C" relationship:

• Symmetric: if C(hFoo, hBar), then C(hBar, hFoo).
• Transitive: if C(hFoo, hBar) and C(hFoo, hBaz), then C(hBar, hBaz).

In short, "C" is an equivalence relationship.