


Next: Free Energy of Conformational
Up: Additional Simulation Parameters
Previous: Pressure Control
Contents
Subsections
There are several ways to apply external forces to simulations with NAMD.
These are described below.
NAMD provides the ability to apply constant forces to some atoms.
There are two parameters that control this feature.
NAMD provides the ability to apply a constant electric field to the molecular
system being simulated.
Energy due to the external field will be reported in the MISC column
and may be discontinuous in simulations using periodic boundary conditions if,
for example, a charged hydrogen group moves outside of the central cell.
There are two parameters that control this feature.
Moving constraints feature works in conjunction with the Harmonic
Constraints (see an appropriate section of the User's guide).
The reference positions of all constraints
will move according to
 |
(1) |
A velocity vector  (movingConsVel) needs to be specified.
(movingConsVel) needs to be specified.
The way the moving constraints work is that the moving reference
position is calculated every integration time step using
Eq. 1, where  is in Å/timestep, and
is in Å/timestep, and  is the
current timestep (i.e., firstTimestep plus however many
timesteps have passed since the beginning of NAMD run). Therefore,
one should be careful when restarting simulations to appropriately
update the firstTimestep parameter in the NAMD configuration
file or the reference position specified in the reference PDB file.
is the
current timestep (i.e., firstTimestep plus however many
timesteps have passed since the beginning of NAMD run). Therefore,
one should be careful when restarting simulations to appropriately
update the firstTimestep parameter in the NAMD configuration
file or the reference position specified in the reference PDB file.
NOTE: NAMD actually calculates the constraints
potential with
 and the force with
and the force with
 ,
where
,
where  is the exponent consexp. The result is that if one
specifies some value for the force constant
is the exponent consexp. The result is that if one
specifies some value for the force constant  in the PDB file,
effectively, the force constant is
in the PDB file,
effectively, the force constant is  in calculations. This caveat
was removed in SMD feature.
in calculations. This caveat
was removed in SMD feature.
The following parameters describe the parameters for the
moving harmonic constraint feature of NAMD.
The constraints parameters are specified in the same manner as for
usual (static) harmonic constraints. The reference positions of all
constrained atoms are then rotated with a given angular velocity
about a given axis. If the force constant of the constraints is
sufficiently
large, the constrained atoms will follow their reference positions.
A rotation matrix 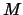 about the axis unit vector
about the axis unit vector  is calculated every
timestep
for the angle of rotation corresponding to the current timestep.
angle =
is calculated every
timestep
for the angle of rotation corresponding to the current timestep.
angle = 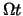 ,
where
,
where  is the angular velocity of rotation.
is the angular velocity of rotation.
From now on, all quantities are 3D vectors, except the matrix 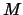 and the
force constant
and the
force constant  .
.
The current reference position 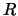 is calculated from the initial
reference
position
is calculated from the initial
reference
position  (at
(at  ),
),
 ,
where
,
where  is the pivot point.
is the pivot point.
Coordinates of point N can be found as
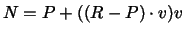 .
Normal from the atom pos to the axis is, similarly,
normal
.
Normal from the atom pos to the axis is, similarly,
normal
 The force is, as usual,
The force is, as usual,
 ;
This is the force applied to the atom in NAMD (see below).
NAMD does not know anything about the torque
applied. However, the torque applied to the atom can be calculated
as a vector product
torque
;
This is the force applied to the atom in NAMD (see below).
NAMD does not know anything about the torque
applied. However, the torque applied to the atom can be calculated
as a vector product
torque
 Finally, the torque applied to the atom with respect to the axis
is the projection of the torque on the axis, i.e.,
Finally, the torque applied to the atom with respect to the axis
is the projection of the torque on the axis, i.e.,
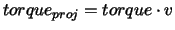
If there are atoms that have to be constrained, but not moved,
this implementation is not suitable, because it will move all
reference positions.
Only one of the moving and rotating constraints can be used at a
time.
Using very soft springs for rotating constraints leads to the system
lagging behind the reference positions, and then the force is applied
along a direction different from the "ideal" direction along the
circular path.
Pulling on N atoms at the same time with a spring of stiffness K
amounts to pulling on the whole system by a spring of stiffness NK,
so the overall behavior of the system is as if you are pulling with a
very stiff spring if N is large.
In both moving and rotating constraints the force constant that you
specify in the constraints pdb file is multiplied by 2 for the force
calculation, i.e., if you specified
 in the pdb
file,
the force actually calculated is
in the pdb
file,
the force actually calculated is
 .
SMD feature of namd2 does the calculation without multiplication of
the
force constant specified in the config file by 2.
.
SMD feature of namd2 does the calculation without multiplication of
the
force constant specified in the config file by 2.
The SMD feature is independent from the harmonic constraints, although it
follows the same ideas. In both SMD and harmonic constraints, one specifies
a PDB file which indicates which atoms are 'tagged' as constrained. The PDB
file also gives initial coordinates for the constraint positions. One also
specifies such parameters as the force constant(s) for the constraints,
and the velocity with which the constraints move.
There are two major differences between SMD and
harmonic constraints:
- In harmonic constraints, each tagged atom is harmonically constrained
to a reference point which moves with constant velocity. In SMD, it is
the center of mass of the tagged atoms which is constrained to move
with constant velocity.
- In harmonic constraints, each tagged atom is constrained in all three
spatial dimensions. In SMD, tagged atoms are constrained only along
the constraint direction.
The center of mass of the SMD atoms will be harmonically constrained with
force constant  (SMDk) to move with velocity
(SMDk) to move with velocity  (SMDVel) in
the direction
(SMDVel) in
the direction 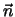 (SMDDir). SMD thus results in the following
potential being applied to the system:
(SMDDir). SMD thus results in the following
potential being applied to the system:
![\begin{displaymath}
U(\vec r_1, \vec r_2, ..., t) \; = \; \frac{1}{2}
k\left[vt - (\vec R(t) - \vec R_0)\cdot \vec n \right]^2.
\end{displaymath}](img63.gif) |
(2) |
Here,
 where
where  is the number of elapsed timesteps
in the simulation and
is the number of elapsed timesteps
in the simulation and  is the size of the timestep in femtoseconds.
Also,
is the size of the timestep in femtoseconds.
Also,  is the current center of mass of the SMD atoms and
is the current center of mass of the SMD atoms and  is
the initial center of mass as defined by the coordinates in SMDFile.
Vector
is
the initial center of mass as defined by the coordinates in SMDFile.
Vector 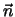 is normalized by NAMD before being used.
is normalized by NAMD before being used.
NAMD provides output of the current SMD data. The frequency of
output is specified by the SMDOutputFreq parameter in the
configuration file. Every SMDOutputFreq timesteps NAMD will
print the current timestep, current position of the center of mass of the
restrained atoms, and
the current force applied to the center of mass (in piconewtons, pN).
The output line starts with word SMD
The following parameters describe the parameters for the
SMD feature of NAMD.
NAMD now works directly with VMD to allow you to view and interactively
steer your simulation. With IMD enabled, you can connect to NAMD at any
time during the simulation to view the current state of the system or perform
interactive steering.
NAMD provides a limited Tcl scripting interface designed for applying forces and performing on-the-fly analysis.
This interface is efficient if only a few coordinates, either of individual atoms or centers of mass of groups of atoms, are needed.
In addition, information must be requested one timestep in advance.
The following configuration parameters are used to enable the Tcl interface:
At this point only low-level commands are defined.
In the future this list will be expanded. Current commands are:
- print <anything>
This command should be used instead of puts to display output.
For example, ``SPMampprint Hello World&''.
- atomid <segname> <resid> <atomname>
Determines atomid of an atom from its segment, residue, and name.
For example, ``atomid br 2 N''.
- addatom <atomid>
Request coordinates of this atom for next force evaluation.
Request remains in effect until clearconfig is called.
For example, ``addatom 4'' or ``addatom [atomid br 2 N]''.
- addgroup <atomid list>
Request center of mass coordinates of this group for next force evaluation.
Returns a group ID which is of the form gN where N is a small integer.
This group ID may then be used to find coordinates and apply forces just like a regular atom ID.
Aggregate forces may then be applied to the group as whole.
Request remains in effect until clearconfig is called.
For example, ``set groupid [addgroup { 14 10 12 }]''.
- clearconfig
Clears the current list of requested atoms. After clearconfig,
calls to addatom and addgroup can be used to build a new
configuration.
- loadcoords <varname>
Loads requested atom and group coordinates (in Å) into a local array.
loadcoords should only be called from within the calcforces procedure.
For example, ``loadcoords p'' and ``print p(4)''.
- loadforces <varname>
Loads the forces applied in the previous timestep (in kcal mol Å
Å ) into a local array.
loadforces should only be called from within the calcforces procedure.
For example, ``loadforces f'' and ``print f(4)''.
) into a local array.
loadforces should only be called from within the calcforces procedure.
For example, ``loadforces f'' and ``print f(4)''.
- loadmasses <varname>
Loads requested atom and group masses (in amu) into a local array.
loadmasses should only be called from within the calcforces procedure.
For example, ``loadcoords m'' and ``print m(4)''.
- addforce <atomid|groupid> <force vector>
Applies force (in kcal mol Å
Å ) to atom or group.
addforce should only be called from within the calcforces procedure.
For example, ``
) to atom or group.
addforce should only be called from within the calcforces procedure.
For example, ``addforce $groupid { 1. 0. 2. }''.
Several vector routines from the VMD Tcl interface are also defined.



Next: Free Energy of Conformational
Up: Additional Simulation Parameters
Previous: Pressure Control
Contents
namd@ks.uiuc.edu