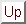



Next: Gaussian Accelerated Molecular Dynamics
Up: Accelerated Sampling Methods
Previous: Accelerated Sampling Methods
Contents
Index
Subsections
Accelerated Molecular Dynamics
Accelerated molecular dynamics (aMD) [38] is an enhanced-sampling method that
improves the conformational space sampling by
reducing energy barriers separating different states of a system.
The method modifies the potential
energy landscape by raising energy wells that are below
a certain threshold level, while leaving those above this level unaffected.
As a result, barriers separating adjacent energy basins are reduced, allowing the system to sample
conformational space that cannot be easily accessed in a classical MD simulation.
Please include the following two references in your work using the NAMD implementation of aMD:
- Accelerated Molecular Dynamics: A Promising and Efficient Simulation Method for Biomolecules, D.Hamelberg, J.Mongan, and J.A. McCammon. J. Chem. Phys., 120:11919-11929, 2004.
- Implementation of Accelerated Molecular Dynamics in NAMD, Y.Wang, C.Harrison, K.Schulten, and J.A. McCammon, Comp. Sci. Discov., 4:015002, 2011.
In the original form of aMD [38], when the system's potential energy falls
below a threshold energy, 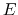 , a boost potential is added,
such that the modified potential,
, a boost potential is added,
such that the modified potential,
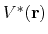 , is related to the original
potential,
, is related to the original
potential,
 , via
, via
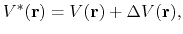 |
(70) |
where
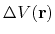 is the boost potential,
is the boost potential,
 |
(71) |
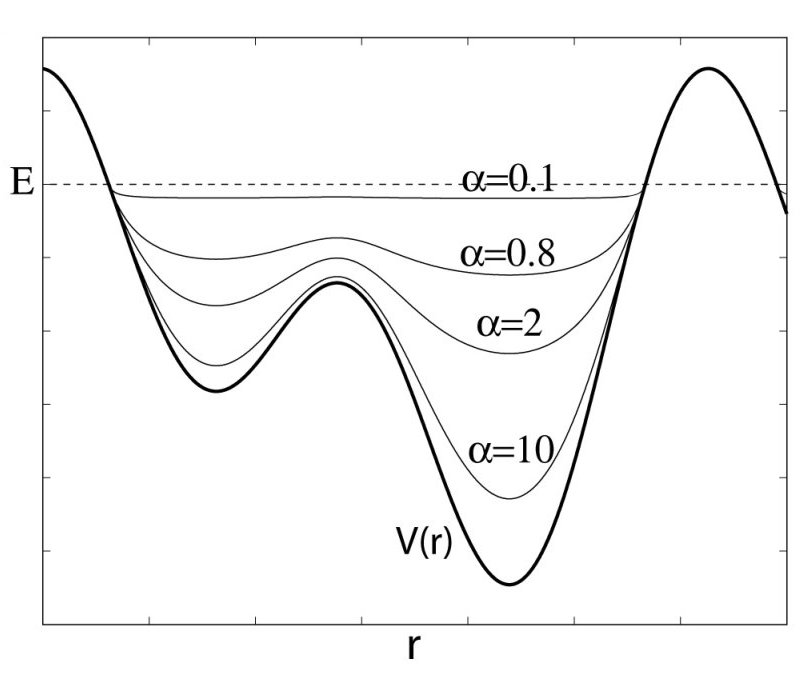
As shown in the following figure, the threshold energy 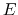 controls the portion of
the potential surface affected by the boost, while the acceleration factor
controls the portion of
the potential surface affected by the boost, while the acceleration factor
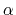 determines the shape of the modified potential.
Note that
determines the shape of the modified potential.
Note that 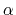 cannot be set to zero, otherwise the derivative of the modified potential
is discontinuous.
cannot be set to zero, otherwise the derivative of the modified potential
is discontinuous.
Figure:
Schematics of the aMD method. When the original potential (thick line) falls below a threshold energy 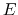 (dashed line),
a boost potential is added. The modified energy profiles (thin lines) have smaller barriers separating adjacent
energy basins.
(dashed line),
a boost potential is added. The modified energy profiles (thin lines) have smaller barriers separating adjacent
energy basins.
|
|
From an aMD simulation, the ensemble average,
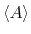 , of an observable,
, of an observable,
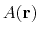 , can be calculated
using the following reweighting procedure:
, can be calculated
using the following reweighting procedure:
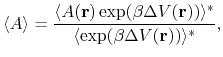 |
(72) |
in which 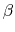 =
=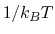 , and
, and
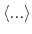 and
and
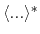 represent
the ensemble average in the original and the aMD ensembles, respectively.
represent
the ensemble average in the original and the aMD ensembles, respectively.
Currently, aMD can be applied in three modes in NAMD: aMDd, aMDT, and aMDdual [104]. The boost energy
is applied to the dihedral potential in the aMDd mode (the default mode), and to the total potential in the aMDT mode.
In the dual boost mode (aMDdual) [37], two independent boost energies are applied, one on the dihedral potential and the other
on the (Total - Dihedral) potential.
The following parameters are used to enable accelerated MD:
- accelMD
 Is accelerated molecular dynamics active?
Is accelerated molecular dynamics active? 
Acceptable Values: on or off
Default Value: off
Description: Specifies if accelerated MD is active.
- accelMDdihe
 Apply boost to dihedrals?
Apply boost to dihedrals? 
Acceptable Values: on or off
Default Value: on
Description: Only applies boost to the dihedral potential.
By default, accelMDdihe is turned on and the boost energy is applied to the dihedral potential of the simulated system.
When accelMDdihe is turned off, aMD switches to the accelMDT mode, and the boost is applied to the total potential.
- accelMDE
 Threshold energy
Threshold energy 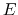
Acceptable Values: Real number
Description: Specifies the threshold energy 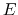 in the aMD equations.
in the aMD equations.
- accelMDalpha
 Acceleration factor
Acceleration factor 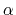
Acceptable Values: Positive real number
Description: Specifies the acceleration factor 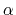 in the aMD equations.
in the aMD equations.
- accelMDdual
 Use dual boost mode?
Use dual boost mode? 
Acceptable Values: on or off
Default Value: off
Description: When accelMDdual is on, aMD switches to the dual boost mode. Two independent boost potentials
will be applied: one to the dihedral potential that is controlled by the parameters accelMDE and accelMDalpha,
and a second to the (Total - Dihedral) potential that is controlled by the accelMDTE and accelMDTalpha parameters described below.
- accelMDTE
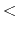 Threshold energy
Threshold energy 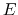 in the dual boost mode
in the dual boost mode 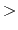
Acceptable Values: Real number
Description: Specifies the threshold energy 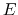 used in the calculation of boost energy for the (Total - Dihedral) potential.
This option is only available when accelMDdual is turned on.
used in the calculation of boost energy for the (Total - Dihedral) potential.
This option is only available when accelMDdual is turned on.
- accelMDTalpha
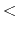 Acceleration factor
Acceleration factor 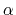 in the dual boost mode
in the dual boost mode 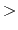
Acceptable Values: Positive real number
Description: Specifies the acceleration factor 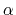 used in the calculation of boost energy for the (Total - Dihedral) potential.
This option is only available when accelMDdual is turned on.
used in the calculation of boost energy for the (Total - Dihedral) potential.
This option is only available when accelMDdual is turned on.
- accelMDFirstStep
 First accelerated MD step
First accelerated MD step 
Acceptable Values: Zero or positive integer
Default Value: 0
Description: Accelerated MD will only be performed when the current step is equal to or higher than accelMDFirstStep, and equal to or lower than accelMDLastStep. Otherwise regular MD will be performed.
- accelMDLastStep
 Last accelerated MD step
Last accelerated MD step 
Acceptable Values: Zero or positive integer
Default Value: 0
Description: Accelerated MD will only be performed when the current step is equal to or higher than accelMDFirstStep, and equal to or lower than accelMDLastStep. Otherwise regular MD will be performed. Note that the accelMDLastStep parameter only has an effect when it is positive. When accelMDLastStep is set to zero (the default), aMD is `open-ended' and will be performed
till the end of the simulation.
- accelMDOutFreq
 Frequency in steps of aMD output
Frequency in steps of aMD output 
Acceptable Values: Positive integer
Default Value: 1
Description: An aMD output line will be printed to the log file at the frequency specified by accelMDOutFreq.
The aMD output will contain the boost potential (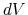 ) at the current timestep,
the average boost potential (
) at the current timestep,
the average boost potential (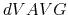 ) since the last aMD output, and various potential energy values at the current timestep.
The boost potential
) since the last aMD output, and various potential energy values at the current timestep.
The boost potential 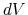 can be used to reconstruct the ensemble average described earlier.
can be used to reconstruct the ensemble average described earlier.




Next: Gaussian Accelerated Molecular Dynamics
Up: Accelerated Sampling Methods
Previous: Accelerated Sampling Methods
Contents
Index
http://www.ks.uiuc.edu/Research/namd/