NAMD configuration parameters

Timestep parameters

• numsteps $<$ number of timesteps $>$
  Acceptable Values: positive integer
  Description: The number of simulation timesteps to be performed. An integer greater than 0 is acceptable. The total amount of simulation time is $\mbox{{\tt numsteps}} \times \mbox{{\tt timestep}}$.

• timestep $<$ timestep size (fs) $>$
  Acceptable Values: non-negative decimal
  Default Value: 1.0
  Description: The timestep size to use when integrating each step of the simulation. The value is specified in femtoseconds.

• firsttimestep $<$ starting timestep value $>$
  Acceptable Values: non-negative integer
  Default Value: 0
  Description: The number of the first timestep. This value is typically used only when a simulation is a continuation of a previous simulation. In this case, rather than having the timestep restart at 0, a specific timestep number can be specified.

• stepspercycle $<$ timesteps per cycle $>$
  Acceptable Values: positive integer
  Default Value: 20
  Description: Number of timesteps in each cycle. Each cycle represents the number of timesteps between atom reassignments. For more details on non-bonded force evaluation, see Section 5.1.

Simulation space partitioning

• cutoff $<$ local interaction distance common to both electrostatic and van der Waals calculations (Å) $>$
  Acceptable Values: positive decimal
  Description: See Section 5.1 for more information.

• switching $<$ use switching function? $>$
  Acceptable Values: on or off
  Default Value: off
  Description: If switching is specified to be off, then a truncated cutoff is performed. If switching is turned on, then smoothing functions are applied to both the electrostatics and van der Waals forces. For a complete description of the non-bonded force parameters see Section 5.1. If switching is set to on, then switchdist must also be defined.

• switchdist $<$ distance at which to activate switching function for electrostatic and van der Waals calculations (Å) $>$
  Acceptable Values: positive decimal 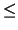$\leq$ cutoff
  Description: Distance at which the switching function should begin to take effect. This parameter only has meaning if switching is set to on. The value of switchdist must be less than or equal to the value of cutoff, since the switching function is only applied on the range from switchdist to cutoff. For a complete description of the non-bonded force parameters see Section 5.1.

• pairlistdist 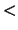$<$ distance between pairs for inclusion in pair lists (Å) $>$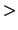
  Acceptable Values: positive decimal 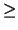$\geq$ cutoff
  Default Value: cutoff
  Description: A pair list is generated each cycle, containing pairs of atoms for which electrostatics and van der Waals interactions will be calculated. This parameter is used when switching is set to on to specify the allowable distance between atoms for inclusion in the pair list. This parameter is equivalent to the X-PLOR parameter CUTNb. If no atom moves more than pairlistdist$-$cutoff during one cycle, then there will be no jump in electrostatic or van der Waals energies when the next pair list is built. Since such a jump is unavoidable when truncation is used, this parameter may only be specified when switching is set to on. If this parameter is not specified and switching is set to on, the value of cutoff is used. A value of at least one greater than cutoff is recommended.

• splitPatch $<$ how to assign atoms to patches $>$
  Acceptable Values: position or hydrogen
  Default Value: hydrogen
  Description: When set to hydrogen, hydrogen atoms are kept on the same patch as their parents, allowing faster distance checking and rigid bonds.

• hgroupCutoff (Å) $<$ used for group-based distance testing $>$
  Acceptable Values: positive decimal
  Default Value: 2.5
  Description: This should be set to twice the largest distance which will ever occur between a hydrogen atom and its mother. Warnings will be printed if this is not the case. This value is also added to the margin.

• margin $<$ extra length in patch dimension (Å) $>$
  Acceptable Values: positive decimal
  Default Value: 0.0
  Description: An internal tuning parameter used in determining the size of the cubes of space with which NAMD uses to partition the system. The value of this parameter will not change the physical results of the simulation. Unless you are very motivated to get the very best possible performance, just leave this value at the default.

Basic dynamics

• exclude $<$ exclusion policy to use $>$
  Acceptable Values: none, 1-2, 1-3, 1-4, or scaled1-4
  Description: This parameter specifies which pairs of bonded atoms should be excluded from non-bonded interactions. With the value of none, no bonded pairs of atoms will be excluded. With the value of 1-2, all atom pairs that are directly connected via a linear bond will be excluded. With the value of 1-3, all 1-2 pairs will be excluded along with all pairs of atoms that are bonded to a common third atom (i.e., if atom A is bonded to atom B and atom B is bonded to atom C, then the atom pair A-C would be excluded). With the value of 1-4, all 1-3 pairs will be excluded along with all pairs connected by a set of two bonds (i.e., if atom A is bonded to atom B, and atom B is bonded to atom C, and atom C is bonded to atom D, then the atom pair A-D would be excluded). With the value of scaled1-4, all 1-3 pairs are excluded and all pairs that match the 1-4 criteria are modified. The electrostatic interactions for such pairs are modified by the constant factor defined by 1-4scaling. The van der Waals interactions are modified by using the special 1-4 parameters defined in the parameter files.

• temperature $<$ initial temperature (K) $>$
  Acceptable Values: positive decimal
  Description: Initial temperature value for the system. Using this option will generate a random velocity distribution for the initial velocities for all the atoms such that the system is at the desired temperature. Either the temperature or the velocities/binvelocities option must be defined to determine an initial set of velocities. Both options cannot be used together.

• COMmotion $<$ allow center of mass motion? $>$
  Acceptable Values: yes or no
  Default Value: no
  Description: Specifies whether or not motion of the center of mass of the entire system is allowed. If this option is set to no, the initial velocities of the system will be adjusted to remove center of mass motion of the system. Note that this does not preclude later center-of-mass motion due to external forces such as random noise in Langevin dynamics, boundary potentials, and harmonic restraints.

• dielectric $<$ dielectric constant for system $>$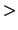
  Acceptable Values: decimal 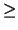$\geq$ 1.0
  Default Value: 1.0
  Description: Dielectric constant for the system. A value of 1.0 implies no modification of the electrostatic interactions. Any larger value will lessen the electrostatic forces acting in the system.

• 1-4scaling 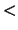$<$ scaling factor for 1-4 interactions $>$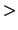
  Acceptable Values: 0 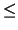$\leq$ decimal 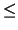$\leq$ 1
  Default Value: 1.0
  Description: Scaling factor for 1-4 interactions. This factor is only used when the exclude parameter is set to scaled1-4. In this case, this factor is used to modify the electrostatic interactions between 1-4 atom pairs. If the exclude parameter is set to anything but scaled1-4, this parameter has no effect regardless of its value.

• seed $<$ random number seed $>$
  Acceptable Values: positive integer
  Default Value: pseudo-random value based on current UNIX clock time
  Description: Number used to seed the random number generator if temperature or langevin is selected. This can be used so that consecutive simulations produce the same results. If no value is specified, NAMD will choose a pseudo-random value based on the current UNIX clock time. The random number seed will be output during the simulation startup so that its value is known and can be reused for subsequent simulations. Note that if Langevin dynamics are used in a parallel simulation (i.e., a simulation using more than one processor) even using the same seed will not guarantee reproducible results.

• rigidBonds $<$ controls if and how ShakeH is used $>$
  Acceptable Values: none, water, all
  Default Value: none
  Description: When rigidBonds is all, the bond between each hydrogen and its mother atom is fixed to the nominal bond length given in the parameter file. When water is selected, only the bonds between the hydrogens and the oxygen in water molecules are constrained. For the default case none, no lengths are constrained.

• rigidTolerance $<$ allowable bond-length error for ShakeH (Å) $>$
  Acceptable Values: positive decimal
  Default Value: 0.00001
  Description: The ShakeH algorithm is assumed to have converged when all constrained bonds differ from the nominal bond length by less than this amount.

• rigidIterations $<$ maximum ShakeH iterations $>$
  Acceptable Values: positive integer
  Default Value: 100
  Description: The maximum number of iterations ShakeH will perform before giving up on constraining the bond lengths. If the bond lengths do not converge, a warning message is printed, and the atoms are left at the final value achieved by ShakeH. Although the default value is 100, convergence is usually reached after fewer than 10 iterations.

DPMTA parameters

DPMTA is no longer included in the released NAMD binaries. We recommend that you instead use PME with a periodic system because it conserves energy better, is more efficient, and is better parallelized. If you must have the fast multipole algorithm you may compile NAMD yourself.

These parameters control the options to DPMTA, an algorithm used to provide full electrostatic interactions. DPMTA is a modified version of the FMA (Fast Multipole Algorithm) and, unfortunately, most of the parameters still refer to FMA rather than DPMTA for historical reasons. Don't be confused!

For a further description of how exactly full electrostatics are incorporated into NAMD, see Section 5.2. For a greater level of detail about DPMTA and the specific meaning of its options, see the DPMTA distribution which is available via anonymous FTP from the site ftp.ee.duke.edu in the directory /pub/SciComp/src.

• FMA $<$ use full electrostatics? $>$
  Acceptable Values: on or off
  Default Value: off
  Description: Specifies whether or not the DPMTA algorithm from Duke University should be used to compute the full electrostatic interactions. If set to on, DPMTA will be used with a multiple timestep integration scheme to provide full electrostatic interactions as detailed in Section 5.2. DPMTA is no longer included in released binaries.

• FMALevels $<$ number of levels to use in multipole expansion $>$
  Acceptable Values: positive integer
  Default Value: 5
  Description: Number of levels to use for the multipole expansion. This parameter is only used if FMA is set to on. A value of 4 should be sufficient for systems with less than 10,000 atoms. A value of 5 or greater should be used for larger systems.

• FMAMp $<$ number of multipole terms to use for FMA $>$
  Acceptable Values: positive integer
  Default Value: 8
  Description: Number of terms to use in the multipole expansion. This parameter is only used if FMA is set to on. If the FMAFFT is set to on, then this value must be a multiple of 4. The default value of 8 should be suitable for most applications.

• FMAFFT $<$ use DPMTA FFT enhancement? $>$
  Acceptable Values: on or off
  Default Value: on
  Description: Specifies whether or not the DPMTA code should use the FFT enhancement feature. This parameter is only used if FMA is set to on. If FMAFFT is set to on, the value of FMAMp must be set to a multiple of 4. This feature offers substantial benefits only for values of FMAMp of 8 or greater. This feature will substantially increase the amount of memory used by DPMTA.

• FMAtheta $<$ DPMTA theta parameter (radians) $>$
  Acceptable Values: decimal
  Default Value: 0.715
  Description: This parameter specifies the value of the theta parameter used in the DPMTA calculation. The default value is based on recommendations by the developers of the code.

• FMAFFTBlock $<$ blocking factor for FMA FFT $>$
  Acceptable Values: positive integer
  Default Value: 4
  Description: The blocking factor for the FFT enhancement to DPMTA. This parameter is only used if both FMA and FMAFFT are set to on. The default value of 4 should be suitable for most applications.

PME parameters

PME stands for Particle Mesh Ewald and is an efficient full electrostatics method for use with periodic boundary conditions. None of the parameters should affect energy conservation, although they may affect the accuracy of the results and momentum conservation.

• PME $<$ Use particle mesh Ewald for electrostatics? $>$
  Acceptable Values: yes or no
  Default Value: no
  Description: Turns on particle mesh Ewald.

• PMETolerance $<$ PME direct space tolerance $>$
  Acceptable Values: positive decimal
  Default Value: $10^{-6}$
  Description: Affects the value of the Ewald coefficient and the overall accuracy of the results.

• PMEInterpOrder $<$ PME interpolation order $>$
  Acceptable Values: positive integer
  Default Value: 4 (cubic)
  Description: Charges are interpolated onto the grid and forces are interpolated off using this many points, equal to the order of the interpolation function plus one.

• PMEGridSizeX $<$ number of grid points in x dimension $>$
  Acceptable Values: positive integer
  Description: The grid size partially determines the accuracy and efficiency of PME. For speed, PMEGridSizeX should have only small integer factors (2, 3 and 5).

• PMEGridSizeY $<$ number of grid points in y dimension $>$
  Acceptable Values: positive integer
  Description: The grid size partially determines the accuracy and efficiency of PME. For speed, PMEGridSizeY should have only small integer factors (2, 3 and 5).

• PMEGridSizeZ $<$ number of grid points in z dimension $>$
  Acceptable Values: positive integer
  Description: The grid size partially determines the accuracy and efficiency of PME. For speed, PMEGridSizeZ should have only small integer factors (2, 3 and 5).

• PMEProcessors $<$ processors for FFT and reciprocal sum $>$
  Acceptable Values: positive integer
  Default Value: larger of x and y grid sizes up to all available processors
  Description: For best performance on some systems and machines, it may be necessary to restrict the amount of parallelism used. Experiment with this parameter if your parallel performance is poor when PME is used.

• useDPME $<$ Use old DPME code? $>$
  Acceptable Values: yes or no
  Default Value: no
  Description: Switches to old DPME implementation of particle mesh Ewald. The new code is faster and allows non-orthogonal cells so you probably just want to leave this option turned off. If you set cellOrigin to something other than $(0,0,0)$ the energy may differ slightly between the old and new implementations. DPME is no longer included in released binaries.

Full direct parameters

The direct computation of electrostatics is not intended to be used during real calculations, but rather as a testing or comparison measure. Because of the 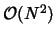${\mathcal O}(N^2)$ computational complexity for performing direct calculations, this is much slower than using DPMTA or PME to compute full electrostatics for large systems. In the case of periodic boundary conditions, the nearest image convention is used rather than a full Ewald sum.

• FullDirect $<$ calculate full electrostatics directly? $>$
  Acceptable Values: yes or no
  Default Value: no
  Description: Specifies whether or not direct computation of full electrostatics should be performed.

Multiple timestep parameters

One of the areas of current research being studied using NAMD is the exploration of better methods for performing multiple timestep integration. Currently the only available method is the impulse-based Verlet-I or r-RESPA method which is stable for timesteps up to 4 fs for long-range electrostatic forces, 2 fs for short-range nonbonded forces, and 1 fs for bonded forces Setting rigid all (i.e., using SHAKE) increases these timesteps to 6 fs, 2 fs, and 2 fs respectively but eliminates bond motion for hydrogen. The mollified impulse method (MOLLY) reduces the resonance which limits the timesteps and thus increases these timesteps to 6 fs, 2 fs, and 1 fs while retaining all bond motion.

• fullElectFrequency $<$ number of timesteps between full electrostatic evaluations $>$
  Acceptable Values: positive integer factor of stepspercycle
  Default Value: nonbondedFreq
  Description: This parameter specifies the number of timesteps between each full electrostatics evaluation. It is recommended that fullElectFrequency be chosen so that the product of fullElectFrequency and timestep does not exceed $4.0$ unless rigidBonds all or molly on is specified, in which case the upper limit is perhaps doubled.

• nonbondedFreq $<$ timesteps between nonbonded evaluation $>$
  Acceptable Values: positive integer factor of fullElectFrequency
  Default Value: 1
  Description: This parameter specifies how often short-range nonbonded interactions should be calculated. Setting nonbondedFreq between 1 and fullElectFrequency allows triple timestepping where, for example, one could evaluate bonded forces every 1 fs, short-range nonbonded forces every 2 fs, and long-range electrostatics every 4 fs.

• MTSAlgorithm $<$ MTS algorithm to be used $>$
  Acceptable Values: impulse/verletI or constant/naive
  Default Value: impulse
  Description: Specifies the multiple timestep algorithm used to integrate the long and short range forces. impulse/verletI is the same as r-RESPA. constant/naive is the stale force extrapolation method.

• longSplitting $<$ how should long and short range forces be split? $>$
  Acceptable Values: xplor, c1
  Default Value: c1
  Description: Specifies the method used to split electrostatic forces between long and short range potentials. The xplor option uses the X-PLOR shifting function, and the c1 splitting uses the following $C^1$ continuous shifting function [5]:
  • $SW(r_{ij}) = 0$ if $\vert{{\vec{r}}_{ij}}\vert > R_{\mathit off}$
  • $SW(r_{ij}) = 1$ if $\vert{{\vec{r}}_{ij}}\vert \leq R_{\mathit on}$
  • if $R_{\mathit off} > \vert{{\vec{r}}_{ij}}\vert \geq R_{\mathit on}$
  where
  • $R_{\mathit on}$ is a constant defined using the configuration value switchdist
  • $R_{\mathit off}$ is specified using the configuration value cutoff

• molly $<$ use mollified impulse method (MOLLY)? $>$
  Acceptable Values: on or off
  Default Value: off
  Description: This method eliminates the components of the long range electrostatic forces which contribute to resonance along bonds to hydrogen atoms, allowing a fullElectFrequency of 6 (vs. 4) with a 1 fs timestep without using rigidBonds all. You may use rigidBonds water but using rigidBonds all with MOLLY makes no sense since the degrees of freedom which MOLLY protects from resonance are already frozen.

• mollyTolerance $<$ allowable error for MOLLY $>$
  Acceptable Values: positive decimal
  Default Value: 0.00001
  Description: Convergence criterion for MOLLY algorithm.

• mollyIterations $<$ maximum MOLLY iterations $>$
  Acceptable Values: positive integer
  Default Value: 100
  Description: Maximum number of iterations for MOLLY algorithm.