Theoretical Paper
- Computer Organization
- Data Structure
- Digital Electronics
- Object Oriented Programming
- Discrete Mathematics
- Graph Theory
- Operating Systems
- Software Engineering
- Computer Graphics
- Database Management System
- Operation Research
- Computer Networking
- Image Processing
- Internet Technologies
- Micro Processor
- E-Commerce & ERP
Practical Paper
Industrial Training
Trees
Trees are non-linear data structures. Trees are encountered frequently in everyday life. In a linked list each node has a link which points to another node. In a tree structure, however, each node may point to several other nodes (which may then point to several other nodes, etc.). Thus a tree is a very flexible and powerful data structure that can be used for a wide variety of applications. For example, suppose we wish to use a data structure to represent a person and all of his or her descendants.
Assume that the person's name is Rahul and that he has 3 children, Sanjay , Sameer and Nisha . Also suppose that Sameer has 3 children, Abhay , Ajit & Madhu and Nisha has one child Neha . We can represent Rahul and his descendants quite naturally with the tree structure shown in Figure 1.

Figure 1.
Notice that each tree node contains a name for data and one or more pointers to the other tree nodes. Although the nodes in a general tree may contain any number of pointers to the other tree nodes, a large number of data-structures have at the most two pointers to the other tree nodes. This type of a tree is called a binary tree. Let us begin our study of binary trees by discussing some basic concepts and terminology. A simple binary tree is shown in Figure 2.
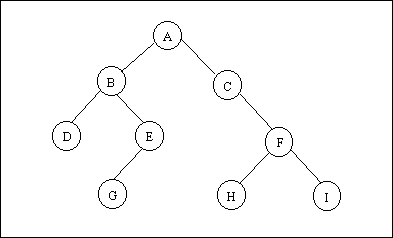
Figure 2.
A binary tree is a finite set of elements that is either empty or is partitioned into three disjoint subsets. The first subset contains a single element called the root of the tree. The other two subsets are themselves binary trees, called the left and right subtrees of the original tree. A left or right subtree can be empty. Each element of a binary tree is called a node of the tree and the tree consists of nine nodes with A as its root. Its left subtree is rooted at B and its right subtree is rooted at C . This is indicated by the two branches emanating from A to B on the left and to C on the right. The absence of a branch indicates an empty subtree. For example, the left subtree of the binary tree rooted at C and the right subtree of the binary tree rooted at E are both empty. The binary trees rooted at D , G , H and I have empty right and left subtrees. Following figure illustrates some structures that are not binary trees. Be sure that you understand why each of them is not a binary tree as just defined.
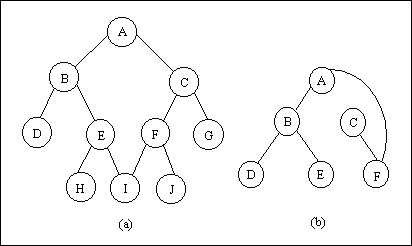
Figure 3.
Let us now get used to some more terminology used in association with binary trees. If A is the root of a binary tree and B is the root of its left or right subtree, then A is said to be the father of B and B is said to be the left or right son of A . A node that has no sons (such as D , G , H , or I of Figure 2.) is called a leaf . In general any node say n1, is an ancestor of node n2 (and n2 is a descendant of n1) if n1 is either the father of n2 or the father of some ancestor of n2 . For example, in the tree of Figure 3, A is an ancestor of C . A node n2 is a left descendant of node n1 if n2 is either the left son of n1 or a descendant of the left son of n1 . A right descendant may be similary defined. Two nodes are brothers if they are left and right sons of the same father. Although natural trees grow with their roots in the ground and their leaves in the air, computer scientists almost universally portray tree data structures with the root at the top and the leaves at the bottom. The direction from the root to the leaves is "down" and the opposite direction is "up". Going from the leaves to the root is called climbing the tree, and going from the root to the leaves is called descending the tree. If every nonleaf node in a binary tree has nonempty left and right subtrees, the tree is termed a strictly binary tree . Thus the tree of Figure 4 is a strictly binary, whereas that of Figure 2 is not a strict binary tree (because nodes C and E have one son each).

Figure 4
The level of a node in a binary tree is defined as follows. The root of the tree has level 0, and the level of any other node in the tree is one more than the level of its father. For example, in the binary tree of Figure 2, node E is at level 2 and node H is at level 3. The depth of a binary tree is the maximum level of any leaf in the tree. This equals the length of the longest path from the root to any leaf. Thus the depth of the tree of Figure 2 is 3. A complete binary tree of depth d is a strictly binary tree all of whose leaves are at level d . Figure 5 illustrates the complete binary tree of depth 3.

Figure 5.
The traversal of a binary tree is to visit each node in the tree exactly once. Binary tree traversal is useful in many applications. The order in which nodes of a linear list are visited is clearly from first to last. However, there is no such natural linear order for the nodes of a tree. The methods differ primarily in the order in which they visit the nodes. There are three popular methods of binary tree traversal. These methods are known as inorder traversal, preorder traversal and postorder traversal. In each of these methods nothing need be done to traverse an empty binary tree. The functions used to traverse a tree using these methods can be kept quite short if we understand the recursive nature of the binary tree. Recall that a binary tree is recursive in that each subtree is really a binary tree itself. Thus traversing a binary tree involves visiting the root node and traversing its left and right subtrees. The only difference among the methods is the order in which these three operations are performed.
To traverse a nonempty binary tree in preorder , we perform the following three operations:
- Visit the root.
- Traverse the left subtree in preorder.
- Traverse the right subtree in preorder.
To traverse a nonempty binary tree in inorder (or symmetric order):
- Traverse the left subtree in inorder.
- Visit the root.
- Traverse the right subtree in inorder.
To traverse a nonempty binary tree in postorder :
- Traverse the left subtree in postorder.
- Traverse the right subtree in postorder.
- Visit the root.
Many algorithms that use binary trees proceed in two phases. The first phase builds a binary tree, and the second traverses the tree. As an example of such an algorithm, consider the following sorting method. Given a list of numbers in an input file, we wish to print them in ascending order. As we read the numbers, they can be inserted into a binary tree such as the one of Figure 6. When a number is compared with the contents of a node in the tree, a left branch is taken if the number is smaller than the contents of the node and a right branch if it is greater or equal to the contents of the node. Thus if the input list is
20 17 6 8 10 20 7 18 13 12 5 6
The binary tree of Figure 6 is produced.

Figure 6
Such a binary tree has the property that all elements in the left subtree of a node n are less than the contents of n, and all elements in the right subtree of n are greater than or equal to the contents of n. A binary tree that has this property is called a Binary Search tree. If a binary search tree is traversed in inorder (left, root, right) and the contents of each node are printed as the node is visited, the numbers are printed in ascending order. Convince yourself that this is the case for the binary search tree of Figure 6. The program to implement this algorithm is given below
/* Program to implement a binary tree */
#include"alloc.h"
struct btreenode
{
struct btreenode *leftchild ;
int data ;
struct btreenode *rightchild ;
} ;

