Home >> PURE MATHS, Differential Calculus, tangents & normals
Tangents |
Tangents
The gradient of the tangent to the curve y = f(x) at the point (x1, y1) on the curve is given by:
the value of dy/dx, when x = x1 and y = y1
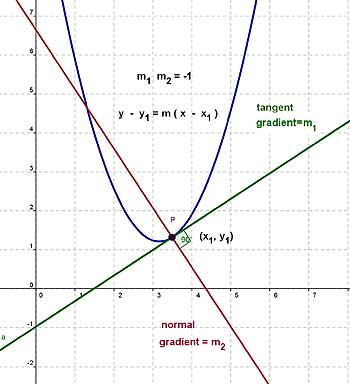
Normals
Two lines of gradients m 1, m 2 respectively are perpendicular to eachother if the product,
![]()
Equation of a Tangent
The equation of a tangent is found using the equation for a straight line of gradient m, passing through the point (x1, y1)

To obtain the equation we substitute in the values for x1 and y1 and m (dy/dx) and rearrange to make y the subject.
Example
Find the equation of the tangent to the curve y = 2x2 at the point (1,2).

Equation of a Normal
The equation of a normal is found in the same way as the tangent.
The gradient(m2) of the normal is calculated from;
![]()
(where m1 is the gradient of the tangent)
so,

Example
Find the equation of the normal to the curve:
y = x2 + 4x + 3, at the point (-1,0).

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
