Êîä Õàôôìàíà
Ñèìàêîâ Àëåêñàíäð
Ñûêòûâêàðñêèé Ãîñóäàðñòâåííûé Óíèâåðñèòåò
Êàôåäðà Ïðèêëàäíîé Ìàòåìàòèêè
Ââåäåíèå
 ýòîé ñòàòüå ìû ðàññìîòðèì îäèí èç ñàìûõ ðàñïðîñòðàíåííûõ ìåòîäîâ ñæàòèÿ äàííûõ. Ðå÷ü ïîéäåò î êîäå Õàôôìàíà (Huffman code) èëè ìèíèìàëüíî-èçáûòî÷íîì ïðåôèêñíîì êîäå (minimum-redundancy prefix code). Ìû íà÷íåì ñ îñíîâíûõ èäåé êîäà Õàôôìàíà, èññëåäóåì ðÿä âàæíûõ ñâîéñòâ è çàòåì ïðèâåäåì ïîëíóþ ðåàëèçàöèþ êîäåðà è äåêîäåðà, ïîñòðîåííûõ íà èäåÿõ, èçëîæåííûõ â ýòîé ñòàòüå.
Èäåÿ, ëåæàùàÿ â îñíîâå êîäà Õàôôìàíà, äîñòàòî÷íî ïðîñòà. Âìåñòî òîãî ÷òîáû êîäèðîâàòü âñå ñèìâîëû îäèíàêîâûì ÷èñëîì áèò (êàê ýòî ñäåëàíî, íàïðèìåð, â ASCII êîäèðîâêå, ãäå íà êàæäûé ñèìâîë îòâîäèòñÿ ðîâíî ïî 8 áèò), áóäåì êîäèðîâàòü ñèìâîëû, êîòîðûå âñòðå÷àþòñÿ ÷àùå, ìåíüøèì ÷èñëîì áèò, ÷åì òå, êîòîðûå âñòðå÷àþòñÿ ðåæå. Áîëåå òîãî, ïîòðåáóåì, ÷òîáû êîä áûë îïòèìàëåí èëè, äðóãèìè ñëîâàìè, ìèíèìàëüíî-èçáûòî÷åí.
Ïåðâûì òàêîé àëãîðèòì îïóáëèêîâàë Äýâèä Õàôôìàí (David Huffman) [1] â 1952 ãîäó. Àëãîðèòì Õàôôìàíà äâóõïðîõîäíûé. Íà ïåðâîì ïðîõîäå ñòðîèòñÿ ÷àñòîòíûé ñëîâàðü è ãåíåðèðóþòñÿ êîäû. Íà âòîðîì ïðîõîäå ïðîèñõîäèò íåïîñðåäñòâåííî êîäèðîâàíèå.
Ñòîèò îòìåòèòü, ÷òî çà 50 ëåò ñî äíÿ îïóáëèêîâàíèÿ, êîä Õàôôìàíà íè÷óòü íå ïîòåðÿë ñâîåé àêòóàëüíîñòè è çíà÷èìîñòè. Òàê ñ óâåðåííîñòüþ ìîæíî ñêàçàòü, ÷òî ìû ñòàëêèâàåìñÿ ñ íèì, â òîé èëè èíîé ôîðìå (äåëî â òîì, ÷òî êîä Õàôôìàíà ðåäêî èñïîëüçóåòñÿ îòäåëüíî, ÷àùå ðàáîòàÿ â ñâÿçêå ñ äðóãèìè àëãîðèòìàìè), ïðàêòè÷åñêè êàæäûé ðàç, êîãäà àðõèâèðóåì ôàéëû, ñìîòðèì ôîòîãðàôèè, ôèëüìû, ïîñûëàåì ôàêñ èëè ñëóøàåì ìóçûêó.
Êîä Õàôôìàíà
Îïðåäåëåíèå 1: Ïóñòü A={a1,a2,...,an} - àëôàâèò èç n ðàçëè÷íûõ ñèìâîëîâ, W={w1,w2,...,wn} - ñîîòâåòñòâóþùèé åìó íàáîð ïîëîæèòåëüíûõ öåëûõ âåñîâ. Òîãäà íàáîð áèíàðíûõ êîäîâ C={c1,c2,...,cn}, òàêîé ÷òî:
| (1) | ci íå ÿâëÿåòñÿ ïðåôèêñîì äëÿ cj, ïðè i!=j |
| (2) | 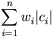 |
ìèíèìàëüíà (|ci| äëèíà êîäà ci) |
Çàìå÷àíèÿ:
- Ñâîéñòâî (1) íàçûâàåòñÿ ñâîéñòâîì ïðåôèêñíîñòè. Îíî ïîçâîëÿåò îäíîçíà÷íî äåêîäèðîâàòü êîäû ïåðåìåííîé äëèíû.
- Ñóììó â ñâîéñòâå (2) ìîæíî òðàêòîâàòü êàê ðàçìåð çàêîäèðîâàííûõ äàííûõ â áèòàõ. Íà ïðàêòèêå ýòî î÷åíü óäîáíî, ò.ê. ïîçâîëÿåò îöåíèòü ñòåïåíü ñæàòèÿ íå ïðèáåãàÿ íåïîñðåäñòâåííî ê êîäèðîâàíèþ.
-  äàëüíåéøåì, ÷òîáû èçáåæàòü íåäîðàçóìåíèé, ïîä êîäîì áóäåì ïîíèìàòü áèòîâóþ ñòðîêó îïðåäåëåííîé äëèíû, à ïîä ìèíèìàëüíî-èçáûòî÷íûì êîäîì èëè êîäîì Õàôôìàíà - ìíîæåñòâî êîäîâ (áèòîâûõ ñòðîê), ñîîòâåòñòâóþùèõ îïðåäåëåííûì ñèìâîëàì è îáëàäàþùèõ îïðåäåëåííûìè ñâîéñòâàìè.
Èçâåñòíî, ÷òî ëþáîìó áèíàðíîìó ïðåôèêñíîìó êîäó ñîîòâåòñòâóåò îïðåäåëåííîå áèíàðíîå äåðåâî.
Îïðåäåëåíèå 2: Áèíàðíîå äåðåâî, ñîîòâåòñòâóþùåå êîäó Õàôôìàíà, áóäåì íàçûâàòü äåðåâîì Õàôôìàíà.
Çàäà÷à ïîñòðîåíèÿ êîäà Õàôôìàíà ðàâíîñèëüíà çàäà÷å ïîñòðîåíèÿ ñîîòâåòñòâóþùåãî åìó äåðåâà. Ïðèâåäåì îáùóþ ñõåìó ïîñòðîåíèÿ äåðåâà Õàôôìàíà:
- Ñîñòàâèì ñïèñîê êîäèðóåìûõ ñèìâîëîâ (ïðè ýòîì áóäåì ðàññìàòðèâàòü êàæäûé ñèìâîë êàê îäíîýëåìåíòíîå áèíàðíîå äåðåâî, âåñ êîòîðîãî ðàâåí âåñó ñèìâîëà).
- Èç ñïèñêà âûáåðåì 2 óçëà ñ íàèìåíüøèì âåñîì.
- Ñôîðìèðóåì íîâûé óçåë è ïðèñîåäèíèì ê íåìó, â êà÷åñòâå äî÷åðíèõ, äâà óçëà âûáðàííûõ èç ñïèñêà. Ïðè ýòîì âåñ ñôîðìèðîâàííîãî óçëà ïîëîæèì ðàâíûì ñóììå âåñîâ äî÷åðíèõ óçëîâ.
- Äîáàâèì ñôîðìèðîâàííûé óçåë ê ñïèñêó.
- Åñëè â ñïèñêå áîëüøå îäíîãî óçëà, òî ïîâòîðèòü 2-5.
Ïðèâåäåì ïðèìåð: ïîñòðîèì äåðåâî Õàôôìàíà äëÿ ñîîáùåíèÿ S="A H F B H C E H E H C E A H D C E E H H H C H H H D E G H G G E H C H H".
Äëÿ íà÷àëà ââåäåì íåñêîëüêî îáîçíà÷åíèé:
- Ñèìâîëû êîäèðóåìîãî àëôàâèòà áóäåì âûäåëÿòü æèðíûì øðèôòîì: A, B, C.
- Âåñà óçëîâ áóäåì îáîçíà÷àòü íèæíèìè èíäåêñàìè: A5, B3, C7.
- Ñîñòàâíûå óçëû áóäåì çàêëþ÷àòü â ñêîáêè: ((A5+B3)8+C7)15.
Èòàê, â íàøåì ñëó÷àå A={A, B, C, D, E, F, G, H}, W={2, 1, 5, 2, 7, 1, 3, 15}.
- A2 B1 C5 D2 E7 F1 G3 H15
- A2 C5 D2 E7 G3 H15 (F1+B1)2
- C5 E7 G3 H15 (F1+B1)2 (A2+D2)4
- C5 E7 H15 (A2+D2)4 ((F1+B1)2+G3)5
- E7 H15 ((F1+B1)2+G3)5 (C5+(A2+D2)4)9
- H15 (C5+(A2+D2)4)9 (((F1+B1)2+G3) 5+E7)12
- H15 ((C5+(A2+D2)4) 9+(((F1+B1)2+G3) 5+E7)12)21
- (((C5+(A2+D2)4) 9+(((F1+B1)2+G3) 5+E7)12)21+H15)36
 ñïèñêå, êàê è òðåáîâàëîñü, îñòàëñÿ âñåãî îäèí óçåë. Äåðåâî Õàôôìàíà ïîñòðîåíî. Òåïåðü çàïèøåì åãî â áîëåå ïðèâû÷íîì äëÿ íàñ âèäå.
ROOT
/\
0 1
/ \
/\ H
/ \
/ \
/ \
0 1
/ \
/ \
/ \
/ \
/\ /\
0 1 0 1
/ \ / \
C /\ /\ E
0 1 0 1
/ \ / \
A D /\ G
0 1
/ \
F B
Ëèñòîâûå óçëû äåðåâà Õàôôìàíà ñîîòâåòñòâóþò ñèìâîëàì êîäèðóåìîãî àëôàâèòà. Ãëóáèíà ëèñòîâûõ óçëîâ ðàâíà äëèíå êîäà ñîîòâåòñòâóþùèõ ñèìâîëîâ.
Ïóòü îò êîðíÿ äåðåâà ê ëèñòîâîìó óçëó ìîæíî ïðåäñòàâèòü â âèäå áèòîâîé ñòðîêè, â êîòîðîé "0" ñîîòâåòñòâóåò âûáîðó ëåâîãî ïîääåðåâà, à "1" - ïðàâîãî. Èñïîëüçóÿ ýòîò ìåõàíèçì, ìû áåç òðóäà ìîæåì ïðèñâîèòü êîäû âñåì ñèìâîëàì êîäèðóåìîãî àëôàâèòà. Âûïèøåì, ê ïðèìåðó, êîäû äëÿ âñåõ ñèìâîëîâ â íàøåì ïðèìåðå:
| A=0010bin | C=000bin | E=011bin | G=0101bin |
| B=01001bin | D=0011bin | F=01000bin | H=1bin |
Òåïåðü ó íàñ åñòü âñå íåîáõîäèìîå äëÿ òîãî ÷òîáû çàêîäèðîâàòü ñîîáùåíèå S. Äîñòàòî÷íî ïðîñòî çàìåíèòü êàæäûé ñèìâîë ñîîòâåòñòâóþùèì åìó êîäîì:
S/="0010 1 01000 01001 1 000 011 1 011 1 000 011 0010 1 0011 000 011 011 1 1 1 000 1 1 1 0011 011 0101 1 0101 0101 011 1 000 1 1".
Îöåíèì òåïåðü ñòåïåíü ñæàòèÿ.  èñõîäíîì ñîîáùåíèè S áûëî 36 ñèìâîëîâ, íà êàæäûé èç êîòîðûõ îòâîäèëîñü ïî [log2|A|]=3 áèòà (çäåñü è äàëåå áóäåì ïîíèìàòü êâàäðàòíûå ñêîáêè [] êàê öåëóþ ÷àñòü, îêðóãëåííóþ â ïîëîæèòåëüíóþ ñòîðîíó, ò.å. [3,018]=4). Òàêèì îáðàçîì, ðàçìåð S ðàâåí 36*3=108 áèò
Ðàçìåð çàêîäèðîâàííîãî ñîîáùåíèÿ S/ ìîæíî ïîëó÷èòü âîñïîëüçîâàâøèñü çàìå÷àíèåì 2 ê îïðåäåëåíèþ 1, èëè íåïîñðåäñòâåííî, ïîäñ÷èòàâ êîëè÷åñòâî áèò â S/. È â òîì è äðóãîì ñëó÷àå ìû ïîëó÷èì 89 áèò.
Èòàê, íàì óäàëîñü ñæàòü 108 â 89 áèò.
Òåïåðü äåêîäèðóåì ñîîáùåíèå S/. Íà÷èíàÿ ñ êîðíÿ äåðåâà áóäåì äâèãàòüñÿ âíèç, âûáèðàÿ ëåâîå ïîääåðåâî, åñëè î÷åðåäíîé áèò â ïîòîêå ðàâåí "0", è ïðàâîå - åñëè "1". Äîéäÿ äî ëèñòîâîãî óçëà ìû äåêîäèðóåì ñîîòâåòñòâóþùèé åìó ñèìâîë.
ßñíî, ÷òî ñëåäóÿ ýòîìó àëãîðèòìó ìû â òî÷íîñòè ïîëó÷èì èñõîäíîå ñîîáùåíèå S.
Êàíîíè÷åñêèé êîä Õàôôìàíà
Êàê ìîæíî áûëî çàìåòèòü èç ïðåäûäóùåãî ðàçäåëà, êîä Õàôôìàíà íå åäèíñòâåíåí. Ìû ìîæåì ïîäâåðãàòü åãî ëþáûì òðàíñôîðìàöèÿì áåç óùåðáà äëÿ ýôôåêòèâíîñòè ïðè ñîáëþäåíèè âñåãî äâóõ óñëîâèé: êîäû äîëæíû îñòàòüñÿ ïðåôèêñíûìè è èõ äëèíû íå äîëæíû èçìåíèòüñÿ.
Îïðåäåëåíèå 3:
Êîä Õàôôìàíà D={d1,d2,...,dn}
íàçûâàåòñÿ êàíîíè÷åñêèì [2], åñëè:
(1) Êîðîòêèå êîäû (åñëè èõ äîïîëíèòü íóëÿìè ñïðàâà) ÷èñëåííî áîëüøå äëèííûõ,
(2) Êîäû îäèíàêîâîé äëèíû ÷èñëåííî âîçðàñòàþò âìåñòå ñ àëôàâèòîì.
Äàëåå, äëÿ êðàòêîñòè, áóäåì íàçûâàòü êàíîíè÷åñêèé êîä Õàôôìàíà ïðîñòî êàíîíè÷åñêèì êîäîì.
Îïðåäåëåíèå 4: Áèíàðíîå äåðåâî, ñîîòâåòñòâóþùåå êàíîíè÷åñêîìó êîäó Õàôôìàíà, áóäåì íàçûâàòü êàíîíè÷åñêèì äåðåâîì Õàôôìàíà.
 êà÷åñòâå ïðèìåðà ïðèâåäåì êàíîíè÷åñêîå äåðåâî Õàôôìàíà äëÿ ñîîáùåíèÿ S, è ñðàâíèì åãî ñ îáû÷íûì äåðåâîì Õàôôìàíà.
ROOT
/\
0 1
/ \
/\ H
/ \
/ \
0 1
/ \
/ \
/ \
/\ /\
/ \ / \
0 1 0 1
/ \ / \
/ \ / \
/\ /\ C E
0 1 0 1
/ \ / \
/\ A D G
0 1
/ \
B F
Âûïèøåì òåïåðü êàíîíè÷åñêèå êîäû äëÿ âñåõ ñèìâîëîâ íàøåãî àëôàâèòà â äâîè÷íîé è äåñÿòè÷íîé ôîðìå. Ïðè ýòîì ñãðóïïèðóåì ñèìâîëû ïî äëèíå êîäà.
| B=00000bin=0dec | A=0001bin=1dec | C=010bin=2dec | H=1bin=1dec |
| F=00001bin=1dec | D=0010bin=2dec | E=011bin=3dec | |
| G=0011bin=3dec |
Óáåäèìñÿ â òîì, ÷òî ñâîéñòâà (1) è (2) èç îïðåäåëåíèÿ 3 âûïîëíÿþòñÿ:
Ðàññìîòðèì, ê ïðèìåðó, äâà ñèìâîëà: E è G. Äîïîëíèì êîä ñèìâîëà E=011bin=3dec (ìàêñèìàëüíàÿ_äëèíà_êîäà-äëèíà_êîäà)=5-3=2 íóëÿìè ñïðàâà: E/=011 00bin=12dec, àíàëîãè÷íî ïîëó÷èì G/=0011 0bin=6dec. Âèäíî ÷òî E/>G/.
Ðàññìîòðèì òåïåðü òðè ñèìâîëà: A, D, G. Âñå îíè èìåþò êîä îäíîé äëèíû. Ëåêñèêîãðàôè÷åñêè A<D<G.  òàêîì æå îòíîøåíèè íàõîäÿòñÿ è èõ êîäû: 1<2<3.
Äàëåå çàìåòèì, ÷òî ïîðÿäêîâûé íîìåð ëþáîãî ëèñòîâîãî óçëà, íà çàíèìàåìîì èì óðîâíå, ÷èñëåííî ðàâåí êîäó ñîîòâåòñòâóþùåãî åìó ñèìâîëà. Ýòî ñâîéñòâî êàíîíè÷åñêèõ êîäîâ íàçûâàþò ÷èñëîâûì (Numerical property).
Ïîÿñíèì âûøåñêàçàííîå íà ïðèìåðå. Ðàññìîòðèì ñèìâîë C. Îí íàõîäèòñÿ íà 3ì óðîâíå (èìååò äëèíó êîäà 3). Åãî ïîðÿäêîâûé íîìåð íà ýòîì óðîâíå ðàâåí 2 (ó÷èòûâàÿ äâà íåëèñòîâûõ óçëà ñëåâà), ò.å. ÷èñëåííî ðàâåí êîäó ñèìâîëà C. Òåïåðü çàïèøåì ýòîò íîìåð â äâîè÷íîé ôîðìå è äîïîëíèì åãî íóëåâûì áèòîì ñëåâà (ò.ê. 2 ïðåäñòàâëÿåòñÿ äâóìÿ áèòàìè, à êîä ñèìâîëà C òðåìÿ): 2dec=10bin=>0 10bin. Ìû ïîëó÷èëè â òî÷íîñòè êîä ñèìâîëà C.
Òàêèì îáðàçîì, ìû ïðèøëè ê î÷åíü âàæíîìó âûâîäó: êàíîíè÷åñêèå êîäû âïîëíå îïðåäåëÿþòñÿ ñâîèìè äëèíàìè. Ýòî ñâîéñòâî êàíîíè÷åñêèõ êîäîâ î÷åíü øèðîêî èñïîëüçóåòñÿ íà ïðàêòèêå. Ìû ê íåìó åùå âåðíåìñÿ.
Òåïåðü âíîâü çàêîäèðóåì ñîîáùåíèå S, íî óæå ïðè ïîìîùè êàíîíè÷åñêèõ êîäîâ:
Z/="0001 1 00001 00000 1 010 011 1 011 1 010 011 0001 1 0010 010 011 011 1 1 1 010 1 1 1 0010 011 0011 1 0011 0011 011 1 010 1 1"
Ò.ê. ìû íå èçìåíèëè äëèí êîäîâ, ðàçìåð çàêîäèðîâàííîãî ñîîáùåíèÿ íå èçìåíèëñÿ: |S/|=|Z/|=89 áèò.
Òåïåðü äåêîäèðóåì ñîîáùåíèå Z/, èñïîëüçóÿ ñâîéñòâà êàíîíè÷åñêèõ êîäîâ.
Ïîñòðîèì òðè ìàññèâà: base[], symb[], offs[]. Ãäå base[i] - êîëè÷åñòâî íåëèñòîâûõ óçëîâ íà óðîâíå i; symb[] - ïåðåñòàíîâêà ñèìâîëîâ àëôàâèòà, îòñîðòèðîâàííàÿ ïî äâóì êëþ÷àì: ïåðâè÷íûé - äëèíà êîäà, âòîðè÷íûé - ëåêñèêîãðàôè÷åñêîå çíà÷åíèå; offs[i] - èíäåêñ ìàññèâà symb[], òàêîé ÷òî symb[offs[i]] ïåðâûé ëèñòîâîé óçåë (ñèìâîë) íà óðîâíå i.
 íàøåì ñëó÷àå: base[0..5]={?, 1, 2, 2, 1, 0}, symb[0..7]={B, F, A, D, G, C, E, H}, offs[0..5]={?, 7, ?, 5, 2, 0}.
Ïðèâåäåì íåñêîëüêî ïîÿñíåíèé. base[0]=? è offs[0]=? íå èñïîëüçóþòñÿ, ò.ê. íåò êîäîâ äëèíû 0, à offs[2]=? - ò.ê. íà âòîðîì óðîâíå íåò ëèñòîâûõ óçëîâ.
Òåïåðü ïðèâåäåì àëãîðèòì äåêîäèðîâàíèÿ (CANONICAL_DECODE) [5]:
- code = ñëåäóþùèé áèò èç ïîòîêà, length = 1
- Ïîêà code < base[length]
code = code << 1
code = code + ñëåäóþùèé áèò èç ïîòîêà
length = length + 1 - symbol = symb[offs[length] + code - base[length]]
Äðóãèìè ñëîâàìè, áóäåì âäâèãàòü ñëåâà â ïåðåìåííóþ code áèò çà áèòîì èç âõîäíîãî ïîòîêà, äî òåõ ïîð, ïîêà code < base[length]. Ïðè ýòîì íà êàæäîé èòåðàöèè áóäåì óâåëè÷èâàòü ïåðåìåííóþ length íà 1 (ò.å. ïðîäâèãàòüñÿ âíèç ïî äåðåâó). Öèêë â (2) îñòàíîâèòñÿ êîãäà ìû îïðåäåëèì äëèíó êîäà (óðîâåíü â äåðåâå, íà êîòîðîì íàõîäèòñÿ èñêîìûé ñèìâîë). Îñòàåòñÿ ëèøü îïðåäåëèòü êàêîé èìåííî ñèìâîë íà ýòîì óðîâíå íàì íóæåí.
Ïðåäïîëîæèì, ÷òî öèêë â (2), ïîñëå íåñêîëüêèõ èòåðàöèé, îñòàíîâèëñÿ.  ýòîì ñëó÷àå âûðàæåíèå (code - base[length]) ñóòü ïîðÿäêîâûé íîìåð èñêîìîãî óçëà (ñèìâîëà) íà óðîâíå length. Ïåðâûé óçåë (ñèìâîë), íàõîäÿùèéñÿ íà óðîâíå length â äåðåâå, ðàñïîëîæåí â ìàññèâå symb[] ïî èíäåêñó offs[length]. Íî íàñ èíòåðåñóåò íå ïåðâûé ñèìâîë, à ñèìâîë ïîä íîìåðîì (code - base[length]). Ïîýòîìó èíäåêñ èñêîìîãî ñèìâîëà â ìàññèâå symb[] ðàâåí (offs[length] + (code - base[length])). Èíà÷å ãîâîðÿ, èñêîìûé ñèìâîë symbol=symb[offs[length] + code - base[length]].
Ïðèâåäåì êîíêðåòíûé ïðèìåð. Ïîëüçóÿñü èçëîæåííûì àëãîðèòìîì äåêîäèðóåì ñîîáùåíèå Z/.
Z/="0001 1 00001 00000 1 010 011 1 011 1 010 011 0001 1 0010 010 011 011 1 1 1 010 1 1 1 0010 011 0011 1 0011 0011 011 1 010 1 1"
- code = 0, length = 1
- code = 0 < base[length] = 1
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 1 + 1 = 2
code = 0 < base[length] = 2
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 2 + 1 = 3
code = 0 < base[length] = 2
code = 0 << 1 = 0
code = 0 + 1 = 1
length = 3 + 1 = 4
code = 1 = base[length] = 1
- symbol = symb[offs[length] = 2 + code = 1 - base[length] = 1] = symb[2] = A
- code = 1, length = 1
- code = 1 = base[length] = 1
- symbol = symb[offs[length] = 7 + code = 1 - base[length] = 1] = symb[7] = H
- code = 0, length = 1
- code = 0 < base[length] = 1
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 1 + 1 = 2
code = 0 < base[length] = 2
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 2 + 1 = 3
code = 0 < base[length] = 2
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 3 + 1 = 4
code = 0 < base[length] = 1
code = 0 << 1 = 0
code = 0 + 1 = 1
length = 4 + 1 = 5
code = 1 > base[length] = 0
- symbol = symb[offs[length] = 0 + code = 1 - base[length] = 0] = symb[1] = F
Èòàê, ìû äåêîäèðîâàëè 3 ïåðâûõ ñèìâîëà: A, H, F. ßñíî, ÷òî ñëåäóÿ ýòîìó àëãîðèòìó ìû ïîëó÷èì â òî÷íîñòè ñîîáùåíèå S.
Ýòî, ïîæàëóé, ñàìûé ïðîñòîé àëãîðèòì äëÿ äåêîäèðîâàíèÿ êàíîíè÷åñêèõ êîäîâ. Ê íåìó ìîæíî ïðèäóìàòü ìàññó óñîâåðøåíñòâîâàíèé. Ïîäðîáíåå î íèõ ìîæíî ïðî÷èòàòü â [5] è [9].
Âû÷èñëåíèå äëèí êîäîâ
Äëÿ òîãî ÷òîáû çàêîäèðîâàòü ñîîáùåíèå íàì íåîáõîäèìî çíàòü êîäû ñèìâîëîâ è èõ äëèíû. Êàê óæå áûëî îòìå÷åíî â ïðåäûäóùåì ðàçäåëå, êàíîíè÷åñêèå êîäû âïîëíå îïðåäåëÿþòñÿ ñâîèìè äëèíàìè. Òàêèì îáðàçîì, íàøà ãëàâíàÿ çàäà÷à çàêëþ÷àåòñÿ â âû÷èñëåíèè äëèí êîäîâ.
Îêàçûâàåòñÿ, ÷òî ýòà çàäà÷à, â ïîäàâëÿþùåì áîëüøèíñòâå ñëó÷àåâ, íå òðåáóåò ïîñòðîåíèÿ äåðåâà Õàôôìàíà â ÿâíîì âèäå. Áîëåå òîãî, àëãîðèòìû èñïîëüçóþùèå âíóòðåííåå (íå ÿâíîå) ïðåäñòàâëåíèå äåðåâà Õàôôìàíà îêàçûâàþòñÿ ãîðàçäî ýôôåêòèâíåå â îòíîøåíèè ñêîðîñòè ðàáîòû è çàòðàò ïàìÿòè.
Íà ñåãîäíÿøíèé äåíü ñóùåñòâóåò ìíîæåñòâî ýôôåêòèâíûõ àëãîðèòìîâ âû÷èñëåíèÿ äëèí êîäîâ ([3], [4]). Ìû îãðàíè÷èìñÿ ðàññìîòðåíèåì ëèøü îäíîãî èç íèõ. Ýòîò àëãîðèòì äîñòàòî÷íî ïðîñò, íî íåñìîòðÿ íà ýòî î÷åíü ïîïóëÿðåí. Îí èñïîëüçóåòñÿ â òàêèõ ïðîãðàììàõ êàê zip, gzip, pkzip, bzip2 è ìíîãèõ äðóãèõ.
Âåðíåìñÿ ê àëãîðèòìó ïîñòðîåíèÿ äåðåâà Õàôôìàíà. Íà êàæäîé èòåðàöèè ìû ïðîèçâîäèëè ëèíåéíûé ïîèñê äâóõ óçëîâ ñ íàèìåíüøèì âåñîì. ßñíî, ÷òî äëÿ ýòîé öåëè áîëüøå ïîäõîäèò î÷åðåäü ïðèîðèòåòîâ, òàêàÿ êàê ïèðàìèäà (ìèíèìàëüíàÿ). Óçåë ñ íàèìåíüøèì âåñîì ïðè ýòîì áóäåò èìåòü íàèâûñøèé ïðèîðèòåò è íàõîäèòüñÿ íà âåðøèíå ïèðàìèäû. Ïðèâåäåì ýòîò àëãîðèòì.
- Âêëþ÷èì âñå êîäèðóåìûå ñèìâîëû â ïèðàìèäó.
- Ïîñëåäîâàòåëüíî èçâëå÷åì èç ïèðàìèäû 2 óçëà (ýòî áóäóò äâà óçëà ñ íàèìåíüøèì âåñîì).
- Ñôîðìèðóåì íîâûé óçåë è ïðèñîåäèíèì ê íåìó, â êà÷åñòâå äî÷åðíèõ, äâà óçëà âçÿòûõ èç ïèðàìèäû. Ïðè ýòîì âåñ ñôîðìèðîâàííîãî óçëà ïîëîæèì ðàâíûì ñóììå âåñîâ äî÷åðíèõ óçëîâ.
- Âêëþ÷èì ñôîðìèðîâàííûé óçåë â ïèðàìèäó.
- Åñëè â ïèðàìèäå áîëüøå îäíîãî óçëà, òî ïîâòîðèòü 2-5.
Áóäåì ñ÷èòàòü, ÷òî äëÿ êàæäîãî óçëà ñîõðàíåí óêàçàòåëü íà åãî ðîäèòåëÿ. Ó êîðíÿ äåðåâà ýòîò óêàçàòåëü ïîëîæèì ðàâíûì NULL. Âûáåðåì òåïåðü ëèñòîâîé óçåë (ñèìâîë) è ñëåäóÿ ñîõðàíåííûì óêàçàòåëÿì áóäåì ïîäíèìàòüñÿ ââåðõ ïî äåðåâó äî òåõ ïîð, ïîêà î÷åðåäíîé óêàçàòåëü íå ñòàíåò ðàâåí NULL. Ïîñëåäíåå óñëîâèå îçíà÷àåò, ÷òî ìû äîáðàëèñü äî êîðíÿ äåðåâà. ßñíî, ÷òî ÷èñëî ïåðåõîäîâ ñ óðîâíÿ íà óðîâåíü ðàâíî ãëóáèíå ëèñòîâîãî óçëà (ñèìâîëà), à ñëåäîâàòåëüíî è äëèíå åãî êîäà. Îáîéäÿ òàêèì îáðàçîì âñå óçëû (ñèìâîëû), ìû ïîëó÷èì äëèíû èõ êîäîâ.
Ìàêñèìàëüíàÿ äëèíà êîäà
Êàê ïðàâèëî, ïðè êîäèðîâàíèè èñïîëüçóåòñÿ òàê íàçûâàåìàÿ êîäîâàÿ êíèãà (CodeBook), ïðîñòàÿ ñòðóêòóðà äàííûõ, ïî ñóòè äâà ìàññèâà: îäèí ñ äëèíàìè, äðóãîé ñ êîäàìè. Äðóãèìè ñëîâàìè, êîä (êàê áèòîâàÿ ñòðîêà) õðàíèòñÿ â ÿ÷åéêå ïàìÿòè èëè ðåãèñòðå ôèêñèðîâàííîãî ðàçìåðà (÷àùå 16, 32 èëè 64). Äëÿ òîãî ÷òîáû íå ïðîèçîøëî ïåðåïîëíåíèå, ìû äîëæíû áûòü óâåðåíû â òîì, ÷òî êîä ïîìåñòèòñÿ â ðåãèñòð.
Îêàçûâàåòñÿ, ÷òî íà N-ñèìâîëüíîì àëôàâèòå ìàêñèìàëüíûé ðàçìåð êîäà ìîæåò äîñòèãàòü (N-1) áèò â äëèíó. Èíà÷å ãîâîðÿ, ïðè N=256 (ðàñïðîñòðàíåííûé âàðèàíò) ìû ìîæåì ïîëó÷èòü êîä â 255 áèò äëèíîé (ïðàâäà äëÿ ýòîãî ôàéë äîëæåí áûòü î÷åíü âåëèê: 2.292654130570773*10^53~=2^177.259)! ßñíî, ÷òî òàêîé êîä â ðåãèñòð íå ïîìåñòèòñÿ è ñ íèì íóæíî ÷òî-òî äåëàòü.
Äëÿ íà÷àëà âûÿñíèì ïðè êàêèõ óñëîâèÿõ âîçíèêàåò ïåðåïîëíåíèå. Ïóñòü ÷àñòîòà i-ãî ñèìâîëà ðàâíà i-ìó ÷èñëó Ôèáîíà÷÷è. Íàïðèìåð: A-1, B-1, C-2, D-3, E-5, F-8, G-13, H-21. Ïîñòðîèì ñîîòâåòñòâóþùåå äåðåâî Õàôôìàíà.
ROOT
/\
/ \
/ \
/\ H
/ \
/ \
/\ G
/ \
/ \
/\ F
/ \
/ \
/\ E
/ \
/ \
/\ D
/ \
/ \
/\ C
/ \
/ \
A B
Òàêîå äåðåâî íàçûâàåòñÿ âûðîæäåííûì. Äëÿ òîãî ÷òîáû åãî ïîëó÷èòü ÷àñòîòû ñèìâîëîâ äîëæíû ðàñòè êàê ìèíèìóì êàê ÷èñëà Ôèáîíà÷÷è èëè åùå áûñòðåå. Õîòÿ íà ïðàêòèêå, íà ðåàëüíûõ äàííûõ, òàêîå äåðåâî ïîëó÷èòü ïðàêòè÷åñêè íåâîçìîæíî, åãî î÷åíü ëåãêî ñãåíåðèðîâàòü èñêóññòâåííî.  ëþáîì ñëó÷àå ýòó îïàñíîñòü íóæíî ó÷èòûâàòü.
Ýòó ïðîáëåìó ìîæíî ðåøèòü äâóìÿ ïðèåìëåìûìè ñïîñîáàìè. Ïåðâûé èç íèõ îïèðàåòñÿ íà îäíî èç ñâîéñòâ êàíîíè÷åñêèõ êîäîâ. Äåëî â òîì, ÷òî â êàíîíè÷åñêîì êîäå (áèòîâîé ñòðîêå) íå áîëåå [log2N] ìëàäøèõ áèò ìîãóò áûòü íåíóëÿìè. Äðóãèìè ñëîâàìè, âñå îñòàëüíûå áèòû ìîæíî âîîáùå íå ñîõðàíÿòü, ò.ê. îíè âñåãäà ðàâíû íóëþ.  ñëó÷àå N=256 íàì äîñòàòî÷íî îò êàæäîãî êîäà ñîõðàíÿòü ëèøü ìëàäøèå 8 áèòîâ, ïîäðàçóìåâàÿ âñå îñòàëüíûå áèòû ðàâíûìè íóëþ. Ýòî ðåøàåò ïðîáëåìó, íî ëèøü îò÷àñòè. Ýòî çíà÷èòåëüíî óñëîæíèò è çàìåäëèò êàê êîäèðîâàíèå, òàê è äåêîäèðîâàíèå. Ïîýòîìó ýòîò ñïîñîá ðåäêî ïðèìåíÿåòñÿ íà ïðàêòèêå.
Âòîðîé ñïîñîá çàêëþ÷àåòñÿ â èñêóññòâåííîì îãðàíè÷åíèè äëèí êîäîâ (ëèáî âî âðåìÿ ïîñòðîåíèÿ, ëèáî ïîñëå). Ýòîò ñïîñîá ÿâëÿåòñÿ îáùåïðèíÿòûì, ïîýòîìó ìû îñòàíîâèìñÿ íà íåì áîëåå ïîäðîáíî.
Ñóùåñòâóåò äâà òèïà àëãîðèòìîâ îãðàíè÷èâàþùèõ äëèíû êîäîâ. Ýâðèñòè÷åñêèå (ïðèáëèçèòåëüíûå) è îïòèìàëüíûå. Àëãîðèòìû âòîðîãî òèïà äîñòàòî÷íî ñëîæíû â ðåàëèçàöèè è êàê ïðàâèëî òðåáóþò áîëüøèõ çàòðàò âðåìåíè è ïàìÿòè, ÷åì ïåðâûå. Ýôôåêòèâíîñòü ýâðèñòè÷åñêè-îãðàíè÷åííîãî êîäà îïðåäåëÿåòñÿ åãî îòêëîíåíèåì îò îïòèìàëüíî-îãðàíè÷åííîãî. ×åì ìåíüøå ýòà ðàçíèöà, òåì ëó÷øå. Ñòîèò îòìåòèòü, ÷òî äëÿ íåêîòîðûõ ýâðèñòè÷åñêèõ àëãîðèòìîâ ýòà ðàçíèöà î÷åíü ìàëà ([6], [7], [8]), ê òîìó æå îíè î÷åíü ÷àñòî ãåíåðèðóþò îïòèìàëüíûé êîä (õîòÿ è íå ãàðàíòèðóþò, ÷òî òàê áóäåò âñåãäà). Áîëåå òîãî, ò.ê. íà ïðàêòèêå ïåðåïîëíåíèå ñëó÷àåòñÿ êðàéíå ðåäêî (åñëè òîëüêî íå ïîñòàâëåíî î÷åíü æåñòêîå îãðàíè÷åíèå íà ìàêñèìàëüíóþ äëèíó êîäà), ïðè íåáîëüøîì ðàçìåðå àëôàâèòà öåëåñîîáðàçíåå ïðèìåíÿòü ïðîñòûå è áûñòðûå ýâðèñòè÷åñêèå ìåòîäû.
Ìû ðàññìîòðèì îäèí äîñòàòî÷íî ïðîñòîé è î÷åíü ïîïóëÿðíûé ýâðèñòè÷åñêèé àëãîðèòì. Îí íàøåë ñâîå ïðèìåíåíèå â òàêèõ ïðîãðàììàõ êàê zip, gzip, pkzip, bzip2 è ìíîãèõ äðóãèõ.
Çàäà÷à îãðàíè÷åíèÿ ìàêñèìàëüíîé äëèíû êîäà ýêâèâàëåíòíà çàäà÷å îãðàíè÷åíèÿ âûñîòû äåðåâà Õàôôìàíà. Çàìåòèì, ÷òî ïî ïîñòðîåíèþ ëþáîé íåëèñòîâîé óçåë äåðåâà Õàôôìàíà èìååò ðîâíî äâà ïîòîìêà. Íà êàæäîé èòåðàöèè íàøåãî àëãîðèòìà áóäåì óìåíüøàòü âûñîòó äåðåâà íà 1. Èòàê, ïóñòü L - ìàêñèìàëüíàÿ äëèíà êîäà (âûñîòà äåðåâà) è òðåáóåòñÿ îãðàíè÷èòü åå äî L/ < L. Ïóñòü äàëåå RNi ñàìûé ïðàâûé ëèñòîâîé óçåë íà óðîâíå i, à LNi - ñàìûé ëåâûé.
Íà÷íåì ðàáîòó ñ óðîâíÿ L. Ïåðåìåñòèì óçåë RNL íà ìåñòî ñâîåãî ðîäèòåëÿ. Ò.ê. óçëû èäóò ïàðàìè íàì íåîáõîäèìî íàéòè ìåñòî è äëÿ ñîñåäíîãî ñ RNL óçëà. Äëÿ ýòîãî íàéäåì áëèæàéøèé ê L óðîâåíü j, ñîäåðæàùèé ëèñòîâûå óçëû, òàêîé, ÷òî j < (L-1). Íà ìåñòå LNj ñôîðìèðóåì íåëèñòîâîé óçåë è ïðèñîåäèíèì ê íåìó â êà÷åñòâå äî÷åðíèõ óçåë LNj è îñòàâøèéñÿ áåç ïàðû óçåë ñ óðîâíÿ L. Êî âñåì îñòàâøèìñÿ ïàðàì óçëîâ íà óðîâíå L ïðèìåíèì òàêóþ æå îïåðàöèþ. ßñíî, ÷òî ïåðåðàñïðåäåëèâ òàêèì îáðàçîì óçëû, ìû óìåíüøèëè âûñîòó íàøåãî äåðåâà íà 1. Òåïåðü îíà ðàâíà (L-1). Åñëè òåïåðü L/ < (L-1), òî ïðîäåëàåì òî æå ñàìîå ñ óðîâíåì (L-1) è ò.ä. äî òåõ ïîð, ïîêà òðåáóåìîå îãðàíè÷åíèå íå áóäåò äîñòèãíóòî.
Âåðíåìñÿ ê íàøåìó ïðèìåðó, ãäå L=5. Îãðàíè÷èì ìàêñèìàëüíóþ äëèíó êîäà äî L/=4.
ROOT
/\
/ \
/ \
/\ H
/ \
/ \
/ \
/ \
/ \
/ \
/\ /\
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/\ /\ C E
/ \ / \
/ \ / \
/\ A D G
/ \
/ \
B F
Âèäíî, ÷òî â íàøåì ñëó÷àå RNL=F, j=3, LNj=C. Ñíà÷àëà ïåðåìåñòèì óçåë RNL=F íà ìåñòî ñâîåãî ðîäèòåëÿ.
ROOT
/\
/ \
/ \
/\ H
/ \
/ \
/ \
/ \
/ \
/ \
/\ /\
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/\ /\ C E
/ \ / \
/ \ / \
F A D G
B (íåïàðíûé óçåë)
Òåïåðü íà ìåñòå LNj=C ñôîðìèðóåì íåëèñòîâîé óçåë.
ROOT
/\
/ \
/ \
/\ H
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/\ /\
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/\ /\ /\ E
/ \ / \ / \
/ \ / \ / \
F A D G ? ?
B (íåïàðíûé óçåë)
C (íåïàðíûé óçåë)
Ïðèñîåäèíèì ê ñôîðìèðîâàííîìó óçëó äâà íåïàðíûõ: B è C.
ROOT
/\
/ \
/ \
/\ H
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/\ /\
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/\ /\ /\ E
/ \ / \ / \
/ \ / \ / \
F A D G B C
Òàêèì îáðàçîì, ìû îãðàíè÷èëè ìàêñèìàëüíóþ äëèíó êîäà äî 4. ßñíî, ÷òî èçìåíèâ äëèíû êîäîâ, ìû íåìíîãî ïîòåðÿëè â ýôôåêòèâíîñòè. Òàê ñîîáùåíèå S, çàêîäèðîâàííîå ïðè ïîìîùè òàêîãî êîäà, áóäåò èìåòü ðàçìåð 92 áèòà, ò.å. íà 3 áèòà áîëüøå ïî ñðàâíåíèþ ñ ìèíèìàëüíî-èçáûòî÷íûì êîäîì.
ßñíî, ÷òî ÷åì ñèëüíåå ìû îãðàíè÷èì ìàêñèìàëüíóþ äëèíó êîäà, òåì ìåíåå ýôôåêòèâåí áóäåò êîä. Âûÿñíèì íàñêîëüêî ìîæíî îãðàíè÷èâàòü ìàêñèìàëüíóþ äëèíó êîäà. Î÷åâèäíî ÷òî íå êîðî÷å [log2N] áèò.
Âû÷èñëåíèå êàíîíè÷åñêèõ êîäîâ
Êàê ìû óæå íåîäíîêðàòíî îòìå÷àëè, äëèí êîäîâ äîñòàòî÷íî äëÿ òîãî ÷òîáû ñãåíåðèðîâàòü ñàìè êîäû. Ïîêàæåì êàê ýòî ìîæíî ñäåëàòü. Ïðåäïîëîæèì, ÷òî ìû óæå âû÷èñëèëè äëèíû êîäîâ è ïîäñ÷èòàëè ñêîëüêî êîäîâ êàæäîé äëèíû ó íàñ åñòü. Ïóñòü L - ìàêñèìàëüíàÿ äëèíà êîäà, à Ti - êîëè÷åñòâî êîäîâ äëèíû i.
Âû÷èñëèì Si - íà÷àëüíîå çíà÷åíèå êîäà äëèíû i, äëÿ âñåõ i èç [1..L]
SL = 0 (âñåãäà)
SL-1 = (SL + TL) >> 1
SL-2 = (SL-1 + TL-1) >> 1
...
S1 = 1 (âñåãäà)
Äëÿ íàøåãî ïðèìåðà L = 5, T1 .. 5 = {1, 0, 2 ,3, 2}.
S5 = 00000bin = 0dec
S4 = (S5=0 + T5=2) >> 1 =
(00010bin >> 1) = 0001bin = 1dec
S3 = (S4=1 + T4=3) >> 1 =
(0100bin >> 1) = 010bin = 2dec
S2 = (S3=2 + T3=2) >> 1 =
(100bin >> 1) = 10bin = 2dec
S1 = (S2=2 + T2=0) >> 1 =
(10bin >> 1) = 1bin = 1dec
Âèäíî, ÷òî S5, S4, S3, S1 - â òî÷íîñòè êîäû ñèìâîëîâ B, A, C, H. Ýòè ñèìâîëû îáúåäèíÿåò òî, ÷òî âñå îíè ñòîÿò íà ïåðâîì ìåñòå, êàæäûé íà ñâîåì óðîâíå. Äðóãèìè ñëîâàìè, ìû íàøëè íà÷àëüíîå çíà÷åíèå êîäà äëÿ êàæäîé äëèíû (èëè óðîâíÿ).
Òåïåðü ïðèñâîèì êîäû îñòàëüíûì ñèìâîëàì. Êîä ïåðâîãî ñèìâîëà íà óðîâíå i ðàâåí Si, âòîðîãî Si + 1, òðåòüåãî Si + 2 è ò.ä.
Âûïèøåì îñòàâøèåñÿ êîäû äëÿ íàøåãî ïðèìåðà:
| B = S5 = 00000bin | A = S4 = 0001bin | C = S3 = 010bin | H = S1 = 1bin |
| F = S5 + 1 = 00001bin | D = S4 + 1 = 0010bin | E = S3 + 1 = 011bin | |
| G = S4 + 2 = 0011bin |
Âèäíî, ÷òî ìû ïîëó÷èëè òî÷íî òàêèå æå êîäû, êàê åñëè áû ìû ÿâíî ïîñòðîèëè êàíîíè÷åñêîå äåðåâî Õàôôìàíà.
Ïåðåäà÷à êîäîâîãî äåðåâà
Äëÿ òîãî ÷òîáû çàêîäèðîâàííîå ñîîáùåíèå óäàëîñü äåêîäèðîâàòü, äåêîäåðó íåîáõîäèìî èìåòü òàêîå æå êîäîâîå äåðåâî (â òîé èëè èíîé ôîðìå), êàêîå èñïîëüçîâàëîñü ïðè êîäèðîâàíèè. Ïîýòîìó âìåñòå ñ çàêîäèðîâàííûìè äàííûìè ìû âûíóæäåíû ñîõðàíÿòü ñîîòâåòñòâóþùåå êîäîâîå äåðåâî. ßñíî, ÷òî ÷åì êîìïàêòíåå îíî áóäåò, òåì ëó÷øå.
Ðåøèòü ýòó çàäà÷ó ìîæíî íåñêîëüêèìè ñïîñîáàìè. Ñàìîå î÷åâèäíîå ðåøåíèå - ñîõðàíèòü äåðåâî â ÿâíîì âèäå (ò.å. êàê óïîðÿäî÷åííîå ìíîæåñòâî óçëîâ è óêàçàòåëåé òîãî èëè èíîãî âèäà). Ýòî ïîæàëóé ñàìûé ðàñòî÷èòåëüíûé è íåýôôåêòèâíûé ñïîñîá. Íà ïðàêòèêå îí íå èñïîëüçóåòñÿ.
Ìîæíî ñîõðàíèòü ñïèñîê ÷àñòîò ñèìâîëîâ (ò.å. ÷àñòîòíûé ñëîâàðü). Ñ åãî ïîìîùüþ äåêîäåð áåç òðóäà ñìîæåò ðåêîíñòðóèðîâàòü êîäîâîå äåðåâî. Õîòÿ ýòîò ñïîñîá è ìåíåå ðàñòî÷èòåëåí ÷åì ïðåäûäóùèé, îí íå ÿâëÿåòñÿ íàèëó÷øèì.
Íàêîíåö, ìîæíî èñïîëüçîâàòü îäíî èç ñâîéñòâ êàíîíè÷åñêèõ êîäîâ. Êàê óæå áûëî îòìå÷åíî ðàíåå, êàíîíè÷åñêèå êîäû âïîëíå îïðåäåëÿþòñÿ ñâîèìè äëèíàìè. Äðóãèìè ñëîâàìè, âñå ÷òî íåîáõîäèìî äåêîäåðó - ýòî ñïèñîê äëèí êîäîâ ñèìâîëîâ. Ó÷èòûâàÿ, ÷òî â ñðåäíåì äëèíó îäíîãî êîäà äëÿ N-ñèìâîëüíîãî àëôàâèòà ìîæíî çàêîäèðîâàòü [(log2(log2N))] áèòàìè, ïîëó÷èì î÷åíü ýôôåêòèâíûé àëãîðèòì. Íà íåì ìû îñòàíîâèìñÿ ïîäðîáíåå.
Ïðåäïîëîæèì, ÷òî ðàçìåð àëôàâèòà N=256, è ìû ñæèìàåì îáûêíîâåííûé òåêñòîâûé ôàéë (ASCII). Ñêîðåå âñåãî ìû íå âñòðåòèì âñå N ñèìâîëîâ íàøåãî àëôàâèòà â òàêîì ôàéëå. Ïîëîæèì òîãäà äëèíó êîäà îòñóòâóþùèõ ñèìâîëîâ ðàâíîé íóëþ.  ýòîì ñëó÷àå ñîõðàíÿåìûé ñïèñîê äëèí êîäîâ áóäåò ñîäåðæàòü äîñòàòî÷íî áîëüøîå ÷èñëî íóëåé (äëèí êîäîâ îòñóòñòâóþùèõ ñèìâîëîâ) ñãðóïïèðîâàííûõ âìåñòå. Êàæäóþ òàêóþ ãðóïïó ìîæíî ñæàòü ïðè ïîìîùè òàê íàçûâàåìîãî ãðóïïîâîãî êîäèðîâàíèÿ - RLE (Run - Length - Encoding). Ýòîò àëãîðèòì ÷ðåçâû÷àéíî ïðîñò. Âìåñòî ïîñëåäîâàòåëüíîñòè èç M îäèíàêîâûõ ýëåìåíòîâ èäóùèõ ïîäðÿä, áóäåì ñîõðàíÿòü ïåðâûé ýëåìåíò ýòîé ïîñëåäîâàòåëüíîñòè è ÷èñëî åãî ïîâòîðåíèé, ò.å. (M-1). Ïðèìåð: RLE("AAAABBBCDDDDDDD")=A3 B2 C0 D6.
Áîëåå òîãî, ýòîò ìåòîä ìîæíî íåñêîëüêî ðàñøèðèòü. Ìû ìîæåì ïðèìåíèòü àëãîðèòì RLE íå òîëüêî ê ãðóïïàì íóëåâûõ äëèí, íî è êî âñåì îñòàëüíûì. Òàêîé ñïîñîá ïåðåäà÷è êîäîâîãî äåðåâà ÿâëÿåòñÿ îáùåïðèíÿòûì è ïðèìåíÿåòñÿ â áîëüøèíñòâå ñîâðåìåííûõ ðåàëèçàöèé.
Ðåàëèçàöèÿ: SHCODEC
Áîëüøèíñòâî èäåé, èçëîæåííûõ â ýòîé ñòàòüå, ëåãëè â îñíîâó ïðîãðàììû SHCODEC (Static Huffman COder / DECoder). SHCODEC - ÿâëÿåòñÿ ñâîáîäíî-ðàñïðîñòðàíÿåìîé ïðîãðàììîé (freeware). Ïðîãðàììó, èñõîäíûé êîä, äîêóìåíòàöèþ, à òàê æå ðåçóëüòàòû èñïûòàíèé ìîæíî íàéòè òóò: http://www.webcenter.ru/~xander
Ïðèëîæåíèå: áèîãðàôèÿ Ä. Õàôôìàíà
 |
Äýâèä Õàôôìàí ðîäèëñÿ â 1925 ãîäó â øòàòå Îãàéî (Ohio), ÑØÀ.
Õàôôìàí ïîëó÷èë ñòåïåíü áàêàëàâðà ýëåêòðîòåõíèêè â ãîñóäàðñòâåííîì óíèâåðñèòåòå Îãàéî (Ohio State University)
â âîçðàñòå 18 ëåò. Çàòåì îí ñëóæèë â àðìèè îôèöåðîì ïîääåðæêè ðàäàðà íà ýñìèíöå, êîòîðûé ïîìîãàë îáåçâðåæèâàòü
ìèíû â ÿïîíñêèõ è êèòàéñêèõ âîäàõ ïîñëå Âòîðîé Ìèðîâîé Âîéíû.  ïîñëåäñòâèè îí ïîëó÷èë ñòåïåíü ìàãèñòðà â
óíèâåðñèòåòå Îãàéî è ñòåïåíü äîêòîðà â Ìàññà÷óñåòñêîì Èíñòèòóòå Òåõíîëîãèé
(Massachusetts Institute of Technology - MIT).
Õîòÿ Õàôôìàí áîëüøå èçâåñòåí çà ðàçðàáîòêó ìåòîäà ïîñòðîåíèÿ ìèíèìàëüíî-èçáûòî÷íûõ êîäîâ, îí òàê æå ñäåëàë âàæíûé
âêëàä âî ìíîæåñòâî äðóãèõ îáëàñòåé (ïî áîëüøåé ÷àñòè â ýëåêòðîíèêå). Îí äîëãîå âðåìÿ âîçãëàâëÿë êàôåäðó
Êîìïüþòåðíûõ Íàóê â MIT.  1974, áóäó÷è óæå çàñëóæåííûì ïðîôåññîðîì, îí ïîäàë â îòñòàâêó.
Õàôôìàí ïîëó÷èë ðÿä öåííûõ íàãðàä.  1999 - Ìåäàëü Ðè÷àðäà Õàììèíãà (Richard W. Hamming Medal) îò Èíñòèòóòà Èíæåíåðîâ
Ýëåêòðè÷åñòâà è Ýëåêòðîíèêè (Institute of Electrical and Electronics Engineers - IEEE) çà èñêëþ÷èòåëüíûé âêëàä
â Òåîðèþ Èíôîðìàöèè, Ìåäàëü Louis E. Levy îò Ôðàíêëèíñêîãî Èíñòèòóòà (Franklin Institute) çà åãî äîêòîðñêóþ
äèññåðòàöèþ î ïîñëåäîâàòåëüíî ïåðåêëþ÷àþùèõñÿ ñõåìàõ, Íàãðàäó W. Wallace McDowell, Íàãðàäó îò Êîìïüþòåðíîãî
Ñîîáùåñòâà IEEE, Çîëîòóþ þáèëåéíóþ íàãðàäó çà òåõíîëîãè÷åñêèå íîâøåñòâà îò IEEE â 1998.
 îêòÿáðå 1999 ãîäà, â âîçðàñòå 74 ëåò Äýâèä Õàôôìàí ñêîí÷àëñÿ îò ðàêà.
|
Ñïèñîê ëèòåðàòóðû
[1] D.A. Huffman, "A method for the construction of minimum-redundancy codes", Proc. Inst. Radio Engineers, vol. 40, no. 9, pp. 1098-1101, Sep. 1952. [Ñêà÷àòü]
[2] E.S. Schwartz, B. Kallick, "Generating a canonical prefix encoding", Communications of the ACM, vol. 7, no. 3, pp. 166-169, Mar. 1964.
[3] J.V. Leeuwen, "On the construction of Huffman trees", Proc. 3rd International Colloquium on Automata, Languages, and Programming, Edinburgh University, pp. 382-410 July 1976.
[4] J. Katajainen, A. Moffat, "In-place calculation of minimum-redundancy codes", Proc. Workshop on Algorithms and Data Structures, pp. 393-402, Aug. 1995. [Ñêà÷àòü]
[5] A. Moffat, A. Turpin, "On the implementation of minimum-redundancy prefix codes", IEEE Transactions on Communications, vol. 45, no. 10, pp. 1200-1207, June 1997. [Ñêà÷àòü]
[6] R.L. Milidiu, E.S. Laber,"The warm-up algorithm: A Lagrangean construction of length restricted Huffman codes", TR-15, Departmento de Informatica, PUC-RJ, 1997. [Ñêà÷àòü]
[7] R.L. Milidiu, A.A. Pessoa, E.S. Laber, "Efficient implementation of the warm-up algorithm for the construction of length-restricted prefix codes", Proc. of ALENEX (International Workshop on Algorithm Engineering and Experimentation), pp. 1-17, Springer, Jan. 1999. [Ñêà÷àòü]
[8] R.L. Milidiu, A.A. Pessoa, E.S. Laber, "In-place length-restricted prefix coding", Proc. of SPIRE (String Processing and Information Retrieval), pp. 50-59, IEEE Computer Society, Jan. 1998. [Ñêà÷àòü]
[9] D.S. Hirschberg, D.A. Lelewer, "Efficient decoding of prefix codes", Communications of the ACM, vol. 33, no. 4, pp. 449-459, Apr. 1990. [Ñêà÷àòü]
[10] D.A. Lelewer, D.S. Hirschberg, "Data compression", Computing Surveys, vol. 19, no. 3, pp. 261-296, Sep. 1987. [Ñêà÷àòü]
|
Ñèìàêîâ Àëåêñàíäð, Îêòÿáðü 2002 xander@online.ru |

|