It can be difficult to achieve realistic lighting by manually placing light sources in a 3D scene. One way to quickly achieve complex and natural lighting is by using real-world light data to lighten the scene.
In order to do that, you need light data from all directions, that is, a full panoramic view. Since you most likely will be looking directly at a light source at some points on your full panorama, you’ll also need to store data that can handle a large dynamic range – 8 bits are not enough.
A common format for these maps is the equirectangular (aka longitude/latitude) format. These are simple 2D bitmaps, typically in 2:1 format, where the x axis covers 360 degrees of azimuthal (longitude) angles, and the y axis covers 180 degrees of elevation (latitude). They are often stored in RGBE (.HDR) files. A good source of free panoramic HDR’s for Image Based Lighting is the sIBL archive.
Backgrounds and reflections
It is very easy to do reflection mapping using equirectangular maps. Simply look up the reflected ray in the equirectangular map. The conversion from 3D direction to map indices is straight-forward:
vec3 equirectangularMap(vec3 dir, sampler2D sampler) {
// Convert (normalized) dir to spherical coordinates.
vec2 longlat = vec2(atan(dir.y,dir.x),acos(dir.z));
// Normalize, and lookup in equirectangular map.
return texture2D(sampler,longlat/vec2(2.0*PI,PI)).xyz;
}
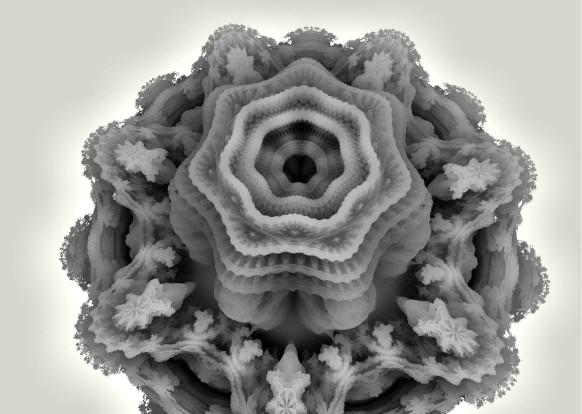
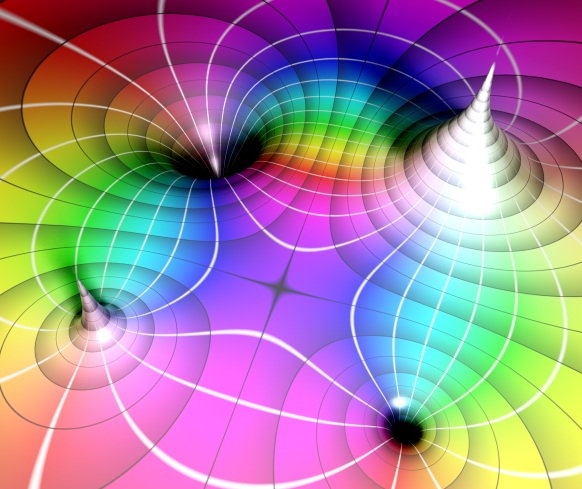
This can also be used to embed the scene in a panoramic view, by looking up the camera ray direction for points that do not hit anything. Here is an example image where reflections and background is sampled from an environment map:

No light model was used in the above image – just pure reflection mapping.
Diffuse light
So what about the diffuse light? Normally, this is modelled by a Lambertian term: the diffuse intensity is proportional to the cosine of the angle between the surface normal and light source direction. In principle, we need to calculate the angle to all points on the hemisphere pointing in the direction of the surface normal, and sum all these contributions. This means, that for each each pixel we raytrace, we need to sample half (one hemisphere) of the pixels in the equirectangular map. Much to slow for even a modern GPU.
But here is the interesting part: the diffuse light contribution is only a function of the surface normal direction. This means we can precalculate the diffuse light in a given normal direction, and store this in a new equirectangular map. Mathematically, this filtering is called a cosine convolution, and some HDR panorama providers are nice enough to provide prefiltered maps for diffuse light (for instance all those in the sIBL archive).
Here is an example of some spheres rendered with specular and diffuse light maps. The materials are faded from pure diffuse (left) to pure specular (right).

As we saw earlier, pure reflection is easy to achieve. But it is also possible to use the Phong reflection model (or other models) with image based lighting. In the Phong model, the specular light intensity depends on the angle between the light source and reflected camera ray. The intensity is proportional to the cosine of this angle raised to a power, which controls the smoothness. Again it is possible to precalculate a convoluted map using the cosine raised to the appropriate power.
Shadows and ground planes
In order to do proper shadows, we would have to check whether the path to every single point on the light map was occluded. Again, this is not feasible. One way to work around this, is to place a single directional light source and then check whether we have a clear to this particular light source. This works nicely, if the light map has a single dominant light source, such as a sun.
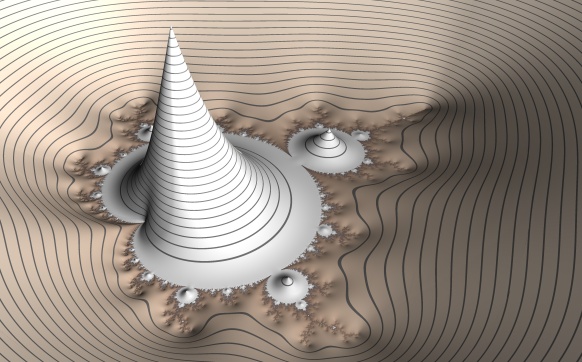
But a problem arise since we do not have any background objects to cast shadows on – the objects in the environment map are placed an infinite distance away, and we don’t know their geometry. Consider this image:

There is no sense of the positioning of the objects in this scene – they seem to float at undefinable locations.
To improve this, we can introduce a ground plane, an invisible object, whose only purpose is to catch shadows.
In Fragmentariums IBL-raytracer, you can enable this under the floor tab. It is also possible to turn on some visual debug, to align the floor with the environment map:

Now, once we have set up the ground plane, we can add some ambient occlusion:

… and some shadows:

In order to sample the shadows, we need to sample the area of the light source uniformly. In the case of a sun-like object, this means sampling a hemisphere in a specified direction and for a given latitude span. A formula for this is given in the Global Illumination Compendium (formula 34). To use this, you need to transform the coordinate system to a new one aligned with the light source direction. I do this:
vec3 getSample(vec3 dir, float extent) {
// Create orthogonal vector (fails for z,y = 0)
vec3 o1 = normalize(vec3(0., -dir.z, dir.y));
vec3 o2 = normalize(cross(dir, o1));
// Convert to spherical coords aligned to dir
vec2 r = getUniformRandomVec2();
r.x=r.x*2.*PI;
r.y=1.0-r.y*extent;
float oneminus = sqrt(1.0-r.y*r.y);
return cos(r.x)*oneminus*o1+sin(r.x)*oneminus*o2+r.y*dir;
}
Here ‘extent’ is the size of the light source we sample. It is given as ‘1-cos(angle)’, so 0 means a point-like light source (sharp shadows) and 1 means a full hemisphere light source (no shadows).
Notice the construction of the aligned coordinate systems fails if ‘dir’ has zero y and z components – if needed, this should be handled as a special case.
Problems with Simple Image Based Lighting
Since no secondary rays are traced for the specular reflections, some geometry ends up with very unrealistic shading:

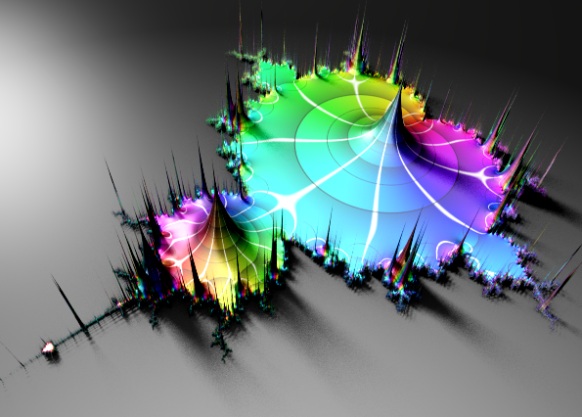
The problems here is that the reflections on the inside on the box sees through the sides. So this simple lighting approach works best for convex objects. Here is another example:
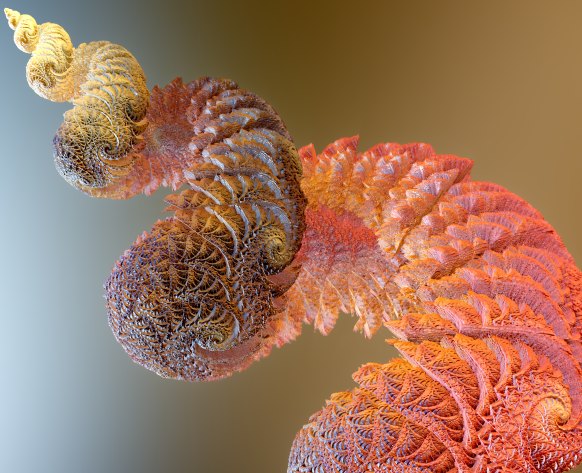
(btw, this is Kali’s dragonKIFS system)
Here again the lighting seems unrealistic – something about the specular light is just wrong.
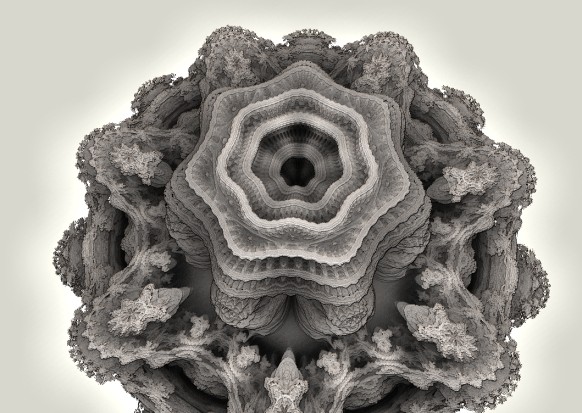
Finally, the combination of the rapidly varying surface normals on a fractal surface and rapidly varying light sources on the environment map introduces new problems. Take a look at this image:

Here there are several small, but strong (HDR) spotlights placed above the Mandelbulb. This image will be very slow to converge and will contain noisy specular highlights: occasionally, one of the subpixel samples will hit a strong light source, which will dominate the sum for the pixel. This will break the sub-pixel anti-aliasing efforts. It is possible to set a maximum (clip) on the specular contributions – or to do HDR tonemapping before averaging – but both solutions goes against the very idea of introducing HDR.
While the specular noise from strong point-like light sources will be difficult to combat, it is easier to do something about the geometry violating reflections.
As of now, I think the best solution is to trace at least secondary rays, and then apply the approximated IBL lighting on the secondary hit points. On problem is that diffuse light does not fall off as quickly as specular light, so you need to sample a lot of points on the hemisphere to get convergence. There are ways around this – for instance, Pixar use bent normals in their Renderman solution, before looking up in the diffuse environment map.
I’ll give a more detailed discussion of the sampling process and the convolution map creation in the next blog post, where I’ll talk about how to speed up diffuse and specular sampling using importance sampling and stratification.
Finally, all the image maps used for lighting on the images accompanying this blog post were from the sIBL archive. And all 3D geometry and composition was of course done in Fragmentarium.