© 2008 Rasmus ehf
and Jóhann Ísak
Inequalities
© 2008 Rasmus ehf |
Inequalities |
|
On the real number line, the distance of the point x from zero is called
the absolute value of x and written as |x|. The two small vertical lines each
side of x is the symbol for absolute value.
If x = 2 the distance of x from zero is written |2| and
has the value 2. So |2| = 2.
If x = −2 the distance of x from zero is written |−2|
and has the value 2. So |−2|
= 2.
Distance, and therefore absolute value, is always a positive number.
The distance between two points, a and b, is b − a if
b > a and a − b if b <
a. If we don’t know which is the larger number we say that the distance
between a and b is |a − b|.
We can think of absolute value as measuring with a ruler. When finding the length of an interval between two points using a ruler, it doesn’t matter whether we measure from left to right or from right to left, the distance is always the same positive number.
Absolute value removes the negative sign from the value we get out of an expression that is in between the absolute value sign.
Draw the graph of the
function f(x) = |x|.
We make a table of values and then plot the graph.
 |
 |
Draw the graph of the function f(x) = |x
− 2| − |x|.
We make a table of values and then
plot the graph.
 |
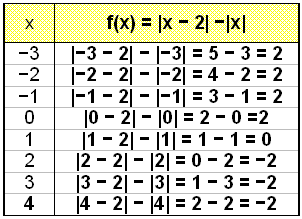Remember
to remove the negative sign when taking the absolute value of a negative
number. |
Notice that the graph is made up of 3 straight lines.
When x < 0 both absolute values contain negative numbers that become
positive when we take the absolute value. We can do this algebraically by
replacing the absolute value sign with a bracket and
multiplying by −1.
When x < 0 the function can be written as follows:
f(x)
= (−1)∙(x − 2) − (−1)∙(x) = −x + 2 + x
= 2
On the interval 0
x < 2 , only the value in the first absolute value term is negative.
Therefore we can write as:
f(x)
= (−1)∙(x − 2) − x = −2x + 2
When x
2 both
absolute value terms contain positive values so nothing needs to be changed. Now
the function can be written as:
f(x)
= (x − 2) − (x) = x − 2 − x = −2
Note that the equation |x − 2| − |x| = 2 is satisfied by all values of x £ 0 whereas the equation |x − 2| − |x| = 0 has only one solution, x = 1.
Solve the inequality |x − 1| < 4.
The important point in this equation is x = 1. This is where the absolute
value sign contains the number 0, is positive if x > 1 but negative when x
< 1. We can think of this as a “turning point” for the equation. The
turning point being where the absolute value changes between being positive and
being negative. This means we can change this absolute value equation into two
simple equations, one that is true when x > 1 and the other true when x <
1. We then solve each one separately.
x < 1 ( change the sign). x > 1 ( sign unchanged).
Complete solution from both
equations:
−3
< x < 5
We will now consider geometrically what the inequality |x − 1| <
4 tells us.
|x − 1| is the distance between x
and the number 1.
|x − 1| < 4 tells us that the distance between x and 1 is less
than 4.
This fits in with the above solution.
Now we will solve the same inequality graphically.
This involves graphing the functions f(x) = |x − 1| and g(x) = 4,
then finding where f(x) lies below (is less than) g(x).
 |
 |
The graph shows that f(x) = |x − 1| lies below the line g(x) = 4 (see the coloured area), on the interval −3 < x < 5.
Solve the inequality |x
+ 2| > |2x − 8|.
Again we solve the problem by looking separately at the
three regions between the x values
that make the expressions between the absolute value signs equal zero.
These points are x
= −2 from the expression on the left hand side and x = 4 from
the expression on the right hand side.
This table shows when the expressions change sign:
Both sides . Right hand side. Unchanged.
 |
|
|
x
> 10 is not a solution because these calculations are valid only for
x < −2. |
 |
Final solution: 2 < x < 10
Now we will solve the equation graphically.
First we make a table of
values for each side of the inequality.
From the graph we see that f(x)
= |x + 2| lies above
g(x) = |2x − 8| between x = 2 and x = 10 (the coloured area).
The solution is therefore 2 < x < 10.
Try Quiz 3 on Inequalities.
Remember to use the checklist to keep track of your work.