Вычислительное мышление: Метод решения сложных задач (fb2)

- Вычислительное мышление: Метод решения сложных задач (пер. Таира Фазильевна Мамедова) 4816K скачать: (fb2) - (epub) - (mobi) - Питер Макоуэн - Пол Керзон

Пол Керзон, Питер Макоуэн
Вычислительное мышление: Метод решения сложных задач

Перевод Таира Мамедова

Редактор Ирина Тулина

Главный редактор С. Турко

Руководитель проекта А. Василенко

Корректоры Е. Аксёнова, О. Улантикова

Компьютерная верстка А. Абрамов

Дизайн обложки Ю. Буга

© World Scientific Publishing Co. Pte. Ltd., 2017

Russian translation arranged with World Scientific Publishing Co. Pte. Ltd., Singapore

© Издание на русском языке, перевод, оформление. ООО «Альпина Паблишер», 2018

Все права защищены. Произведение предназначено исключительно для частного использования. Никакая часть электронного экземпляра данной книги не может быть воспроизведена в какой бы то ни было форме и какими бы то ни было средствами, включая размещение в сети Интернет и в корпоративных сетях, для публичного или коллективного использования без письменного разрешения владельца авторских прав. За нарушение авторских прав законодательством предусмотрена выплата компенсации правообладателя в размере до 5 млн. рублей (ст. 49 ЗОАП), а также уголовная ответственность в виде лишения свободы на срок до 6 лет (ст. 146 УК РФ).

* * *

Предисловие

Всего за несколько десятилетий вычислительное мышление преобразило нашу повседневную жизнь, работу и развлечения. С его помощью мы изменили подход к науке, выигрывали войны, создали целые новые отрасли и спасли много жизней. Именно благодаря вычислительному мышлению ученые решают задачи в области информатики, а значит, оно лежит в основе программирования и остается мощным методом решения проблем как с помощью компьютеров, так и без них. Оно приобрело настолько важную роль, что сегодня во многих странах требуют, чтобы дети осваивали его с младших классов.

В этой книге с помощью фокусов, игр и головоломок, а также настоящих серьезных задач, над которыми работают ученые-информатики, мы объясняем, что такое вычислительное мышление. Мы рассказываем, из каких элементов оно состоит, включая алгоритмическое мышление, декомпозицию, абстракцию, обобщение, рассуждения о логике и сопоставление с образцом, но при этом подчеркиваем необходимость понимания особенностей человека. Мы исследуем связи между вычислительным мышлением, научным мышлением, творческой изобретательностью и инновациями.

Если вы хотите узнать, что такое вычислительное мышление, или ищете новые способы стать эффективнее, начинайте изучать информатику, а если к тому же вы любите математические игры и головоломки, то эта книга для вас. Она позволит вам сделать стартовый рывок в изучении навыков, необходимых и для программирования, и для создания новых технологий в более общем смысле, а также поможет справиться с различными задачами в повседневной жизни. Вы начнете лучше понимать и собственный мозг, и мир цифровых технологий, и наконец, мы покажем вам, как самостоятельно создать цифровой мозг.

Надеемся, что «Вычислительное мышление» увлечет вас и вы будете учиться думать как ученые-информатики.

Об авторах

Пол Керзон – преподаватель информатики Лондонского университета королевы Марии. В его научные интересы входят методика обучения информатике, взаимодействие человека с компьютером и формальные методы. В 2010 г. он стал лауреатом премии для преподавателей, учрежденной Академией высшего образования. В 2007 г. получил приз Совета по инженерным и физическим научным исследованиям как лучший непрофессиональный автор, пишущий о компьютерных науках. Один из основателей ресурса «Преподавание информатики в Лондоне» (Teaching London Computing, www.teachinglondoncomputing.org), который оказывает поддержку преподавателям в непрерывном профессиональном развитии. Самостоятельно освоил программирование, лежа на пляже на юге Франции.

Питер Макоуэн тоже преподаватель информатики Лондонского университета королевы Марии. Среди его научных интересов – машинное зрение, искусственный интеллект и робототехника.

В 2008 г. Питер получил премию для преподавателей, учрежденную Академией высшего образования. В 2011 г. был награжден медалью Маунтбеттена Института инженерного обеспечения и технологий за работу по популяризации информатики среди широкой аудитории. Питер – фокусник-любитель со здоровой тягой к научной фантастике.

Пол и Питер вместе создали проект «Занимательная информатика» (Computer Science for fun, www.cs4fn.org) и стали первыми членами британского объединения «Информатика в учебных заведениях» (Computing at School, CAS). Сейчас Пол – член совета директоров этой организации.

Благодарности

Эта книга – сборник новых материалов и переработанных статей, опубликованных на нашем сайте «Занимательная информатика» (www.cs4fn.org) и на другом нашем сайте «Преподавание информатики в Лондоне» (www.teachinglondoncomputing.org), предназначенном для поддержки учителей.

Мы благодарны Лондонскому университету королевы Марии, который всегда поддерживал нашу работу с общественностью. Все эти годы, пока мы занимались созданием занимательных материалов по информатике, мы получали финансовую поддержку от разных организаций, среди которых Лондонский университет королевы Марии, Совет по инженерным и физическим научным исследованиям (EPSRC), Google, мэрия Лондона, департамент образования, BCS, Исследовательские советы Великобритании (RCUK), Microsoft и ARM.

Нам оказали большую поддержку преподаватели со всей страны и из-за границы. Особую роль сыграли учителя, ученые, представители отрасли и члены нашего объединения «Информатика в учебных заведениях». Они активно содействовали нам и внесли ценный вклад в нашу работу, обмениваясь идеями и тестируя многие из предложенных заданий на практике. Также мы благодарны многим и многим студентам и преподавателям, которых мы в последние десять лет одолевали нашими веселыми занятиями, – за энтузиазм, готовность участвовать и помощь в рождении новых идей. Саймон Пейтон-Джонс из Microsoft Research, Питер Дикман из Google и Билл Митчелл из Британского компьютерного общества невероятно помогли нам. Тим Белл, Куинтин Каттс и команды, разрабатывающие задания по информатике для работы без компьютера в университетах Кентербери и Глазго, стали нашим источником вдохновения – как и многие другие. Задача «Ход конем», в частности, появилась благодаря идее Мацея Сыслё и Анны Беаты Квятковской из Университета Николая Коперника.

Всестороннюю помощь нам оказали сотрудники Лондонского университета королевы Марии. В их числе – Урсула Мартин, Эдмунд Робинсон и Сью Уайт, которые помогли нам запустить ресурс «Занимательная информатика». Габриэлла Казай и Джонатан Блэк очень много сделали на ранних этапах, а Уильям Марш, Джо Броди, Никола Плант, Джейн Уэйт и Тревор Брэгг подключились позднее.

В подростковом возрасте нас особенно вдохновляли развлекательные книги по математике Мартина Гарднера, хотя мы лишь впоследствии поняли, что многие очень интересные вещи на самом деле были информатикой, замаскированной под математику. Мы надеемся, что эта книга подобным образом кого-то вдохновит и позволит сразу же увидеть, что все эти интересные вещи на самом деле информатика. Не дайте себя обмануть, если их назовут математикой!

Мы много и с большой пользой обсуждали математику и фокусы с Мэттом Паркером, Джейсоном Дэвисоном и Ричардом Гэрриоттом. Мы также хотели бы поблагодарить изобретательных фокусников наших дней и былых времен за то, что они придумали хитрые математические трюки с использованием вычислительных алгоритмов, которые мы теперь показываем и преподаем. Это Ник Трост, Дж. Хартман, Пол Гордон, Брент Моррис, Колм Малкехи, Артур Бенджамин, Макс Мэйвен, Альдо Коломбини, Перси Дайаконус, Джон Бэннон и, повторимся, великий ныне покойный Мартин Гарднер. Мы рекомендуем вам посмотреть их работы и больше узнать об алгоритмических фокусах. У них вы найдете удивительные приемы, алгоритмы и идеи для развлечения, а еще, возможно, откроете самый важный секрет: фокусы, не говоря уже о вычислительном мышлении, – замечательное хобби.

Мы никогда бы не оказались там, где находимся сейчас, без замечательных учителей, которые привили нам интерес к разным предметам, и не только к математике и естественным наукам. В той же мере нас вдохновили преподаватели английского, которые внушили нам любовь к литературному труду и помогли понять его.

И больше всего мы благодарны нашим семьям за их огромную поддержку и терпение.

Глава 1
Мышление будущего

Вычислительное мышление – это важный навык, который в информатике осваивают и используют для решения различных задач. Вычислительное мышление настолько важно, что во многих странах его преподают в средних школах. Но в чем же оно состоит? Как оно изменило практически все сферы нашей деятельности? И как использовать его для отдыха и развлечений?

Что с ним делать?

Представьте, что вы ученый и пытаетесь понять поведение птиц, которые ищут корм на земле. Одни кормятся, а другие смотрят в небо, чтобы вовремя увидеть хищника. Как они распределяют роли? Другие ученые тратят время на наблюдения за птицами, но вы идете дальше. Вы придумываете алгоритм – последовательность шагов, – которому должны следовать птицы, чтобы распределить роли. Потом вы создаете компьютерную модель и симулируете сценарии на основе гипотезы, что каждая птица смотрит на своих соседей. Это не только совпадает с результатами ваших наблюдений, но еще и позволяет делать прогнозы, поддающиеся проверке.

Возможно, вы фокусник и у вас появилась идея нового фокуса, основанного на математических свойствах чисел. Вы продумали этапы его представления, однако не уверены, что фокус получится при любых условиях. Вместо того чтобы опробовать его, вы начинаете рассуждать логически и приходите к выводу, что в определенной ситуации все может пойти не так. Внеся некоторые изменения в демонстрацию фокуса, вы гарантируете, что эта ситуация никогда не возникнет.

Вы учитесь в школе, и учитель объясняет, как функционирует мозг. На доске нарисован нейрон и помечены его части, все это нужно запомнить. За вечер вы пишете программу, которая ведет себя как нейрон. Объединив несколько «нейронов» вместе, вы видите, каким образом состоящая из них группа может выполнять какие-то действия. На следующий день с помощью этой программы вы объясняете друзьям, как все работает.

Или, возможно, вы – доктор, которого расстраивают ошибки медицинского персонала при пользовании определенными приборами. Администрация винит сотрудников – одну медсестру только что уволили за такую ошибку. Вы осознаете, что проблема – в устройстве прибора. Занятому человеку легко сделать промах. Вы обращаетесь к производителям и показываете, что небольшие изменения в конструкции гарантируют, что проблема больше никогда не возникнет.

Или, например, вы – учитель и у вас огромная кипа проверенных работ, сложенных в произвольном порядке. Их надо рассортировать, чтобы на родительском собрании можно было быстро найти ту, о которой вы хотите поговорить. Но ничего страшного. Вы знаете, как быстро разложить их по порядку.

Еще один пример. На каникулах вы работаете в кофейне и замечаете, что у вас всегда длинная очередь и это огорчает клиентов. Вы говорите боссу, что сотрудник за кассой проводит много времени в бездействии и отчасти в этом заключается причина задержки. Если вся команда будет работать вместе, то очередь пойдет гораздо быстрее.

Может быть, у вас есть масса идей для игр, в которые вы с удовольствием играли бы с друзьями. Но, в отличие от остальных, вы не просто рассказываете о своих блестящих идеях, а пишете программы на их основе – и через несколько дней уже играете.

Информатика – это не только компьютеры, но и вычисления, которые происходят повсюду. Думайте как программист, и вы начнете подмечать вычисления и видеть возможности усовершенствовать действительность – масса шансов воплотить идеи в реальность.

Навыки для XXI века

Все, кто изучает информатику, получают бонус – осваивают новый фундаментальный тип мышления и способ решения задач. Этот тип мышления абсолютно необходим в новом мире, где высокие технологии повсеместны. Он называется «вычислительное мышление» и является большим преимуществом для тех, кто осваивает информатику, независимо от их будущей профессии. Эта идея получила огромный резонанс, и во многих странах вычислительное мышление добавили к чтению, письму и арифметике в качестве ключевого навыка, который нужно осваивать уже в начальной школе. Благодаря ему компьютеры теперь преобладают во многих сферах нашей жизни и меняют все, чем мы занимаемся, – от слушания музыки до торговли на бирже, от шопинга до науки. Вычислительное мышление дает нам возможность не только высказывать блестящие идеи, но и воплощать их в реальность.

В первый раз словосочетание «вычислительное мышление» использовал педагог и математик Сеймур Паперт. Он предложил обучать математиков совершенно новым способом – с использованием компьютеров. Однако благодаря информатике изменилась не только математика, но и вся наука. Ученый-информатик Дженнет Уинг заявила, что это самый важный компонент в изучении информатики, который надо использовать гораздо шире. Именно она популяризовала термин «вычислительное мышление». Компания Microsoft была настолько впечатлена ее аргументами и важностью поднятой темы, что предоставила Университету Карнеги – Меллон, где работала Уинг, грант в несколько миллионов долларов на создание центра по изучению этого аспекта информатики и его влияния на другие науки.

Так что же такое вычислительное мышление? Это не «то, как думают компьютеры», хотя их все чаще программируют на его использование. Это набор разнообразных человеческих навыков для решения задач. Чтобы их приобрести, необходимо изучать природу вычислительных процессов. Кроме того, необходимы такие определенно важные навыки, как умение творить, ясно объяснять и работать в команде, – но их развивают практически все учебные предметы. Вычислительное мышление заимствует элементы из других типов мышления, например математического и научного. Однако в его основе лежат очень конкретные навыки решения проблем, такие как способность мыслить логически и алгоритмически, не упуская ни одной детали, а также умение находить эффективные способы что-нибудь сделать. Также важную роль играет способность понимать других людей. Информатика уникальна в том плане, что она объединяет все эти разнообразные навыки. Вместе они формируют мощный тип мышления, который меняет мир. Именно благодаря ему мы стали по-новому заниматься наукой, делать покупки, вести бизнес, слушать музыку, играть в игры – в общем, жить по-новому.

Алгоритмическое мышление

Алгоритмическое мышление лежит в основе вычислительного мышления. Оно позволяет находить решения задач нетрадиционным способом. Для специалиста по информатике решить задачу – это не просто получить ответ, например «42». И даже не добиться конкретного результата – например, «я решил судоку из сегодняшнего номера». Решения – это алгоритмы! Алгоритм – просто набор инструкций, которым необходимо следовать. Если точно их выполнять, вы получите собственно ответ на задачу («42») или добьетесь, чего хотите (например, решите судоку). Как только вы получите алгоритмическое решение, вы будете решать подобные задачи вообще не задумываясь, просто «слепо» следуя инструкциям. При наличии такого алгоритма задачу, не углубляясь в суть программы, решит кто угодно. При этом не надо знать или понимать, как в конечном итоге работает алгоритм. Можно даже не иметь представления о том, что вы решаете судоку (и что такое вообще судоку). А это значит, что бездушная машина, компьютер, тоже будет механически следовать инструкциям и решать подобные задачи в любой форме. Именно так и работают компьютеры – они выполняют алгоритмы, написанные людьми.

Настоящая сила этой идеи в том, что следование алгоритму обеспечивает решения для целой группы задач, а не только для одного примера. Алгоритм для решения кроссвордов позволит решить много кроссвордов. Алгоритм для арифметических действий справится с любым расчетом. Когда мы воспринимаем задачи и решения таким образом, это называется алгоритмическое мышление.

Например, недостаточно знать, что 20 + 22 равно 42. Специалисту по информатике нужен алгоритм, который будет складывать два числа. На самом деле все мы в начальной школе изучаем этот алгоритм именно для того, чтобы решать примеры и не углубляться в его составление самим! Подобным образом, во все компьютеры встроена инструкция по сложению – вот насколько она важна! Компьютер действует только как калькулятор, только следуя инструкциям, которые указывают ему, как проводить вычисления. Компьютерная программа – это просто алгоритм или набор алгоритмов, написанных на языке, который понимает машина, – на языке программирования.

Изменить мир

Однако речь здесь идет не только о вычислениях. Алгоритмы можно использовать в самых разных целях. Мыслите алгоритмически, и у вас появится мощный способ изменить мир. Если записать алгоритмы в виде программ, то они будут слепо выполнять все что угодно. Сегодня банки вместо людей используют алгоритмы, чтобы торговать ценными бумагами – покупать, продавать и получать миллионные прибыли. НАСА использует их, чтобы запускать корабли на Марс. Вы пользуетесь алгоритмами, чтобы слушать музыку и смотреть видео. Алгоритмы управляют самолетами, помогают хирургам и позволяют нам делать покупки, сидя у себя в гостиной или в вагоне поезда. Они водят машины и даже создают произведения искусства. Сейчас алгоритмы присутствуют во всех аспектах нашей жизни. Алгоритмы уже преобразили нашу жизнь и продолжают это делать. Поэтому важно понимать, что такое алгоритмическое мышление. Так же, как мы изучаем физику, чтобы понимать физический мир, и биологию – чтобы понимать живой мир, всем нам необходимо в какой-то мере освоить информатику, чтобы понять виртуальный мир, который тихо захватил нашу жизнь.

Научное мышление

Алгоритмическое мышление – это не просто способ решать задачи. Оно открывает новые пути для понимания мира. В традиционной науке используются эксперименты. Биологи ставят эксперименты на крысах и обезьянах, на клеточных культурах. Медики проводят испытания лекарственных препаратов. Физики ставят эксперименты над самим миром. Однако, если мыслить алгоритмически, возможен другой вариант. Если существует теория, объясняющая некое явление, будь то воздействие радиации на поверхность планеты, формирование экосистемы или развитие злокачественной опухоли, мы можем создать алгоритмы, работающие подобным образом. Мы можем создать вычислительную модель – программу, которая должна симулировать интересующие нас феномены, и проводить эксперименты на модели, а не в реальном мире. Если мы правильно понимаем явление, то программа будет вести себя как объект моделирования. Если этого не произойдет, значит, с нашей теорией что-то не так. Обдумывая, что пошло не так, мы обнаружим, чтó надо изменить в теории, и, таким образом, будем лучше понимать явление. Вполне вероятно, что изучение модели выведет нас на новые предположения, которые можно проверить уже в реальном мире.

Вычислительное мышление

Вычислительное мышление подразумевает не только поиск решений в виде алгоритмов. Это целый набор приемов, который обеспечивает нам эффективный способ улучшения жизненных условий и осмысления мира. Но мы не будем погружаться в специфические термины, а продемонстрируем эти методы на примере задач как серьезных (например, помощь инвалидам), так и развлекательных (игры, головоломки и фокусы).

Глава 2
В поисках способа говорить

Одним из самых тяжелых патологических состояний, какие только можно вообразить, является синдром «запертого человека». Человек в таком состоянии полностью парализован и в лучшем случае в состоянии только моргать. Разум заключен в тюрьму бесполезного тела. Человек воспринимает все вокруг, но не может передавать информацию. Тем, кто хотел бы помочь людям с таким синдромом, очевидно, нужно учиться на медиков. Но может ли что-нибудь сделать программист?

Сидром «запертого человека»

Синдром «запертого человека» – это полный паралич тела после инсульта. Вы продолжаете думать, видеть, слышать. Вы так же разумны, как и прежде. Это может случиться с каждым. Лечения этого заболевания нет, поэтому максимум, что могут сделать медики, – позаботиться об удобстве пациента. Но возникает важный вопрос: как помочь пациентам с синдромом «запертого человека» «разговаривать». Как им общаться с врачами, семьей и друзьями? Очевидно, специалист по информатике мог бы изобрести новую технологию, которая была бы полезна в этой ситуации. Однако благодаря вычислительному мышлению мы можем предложить способ гораздо лучше, чем просто «полезная технология».

«Скафандр и бабочка» – невероятно жизнеутверждающая книга. Это автобиография Жан-Доминика Боби, которую он написал после того, как очнулся в больнице полностью парализованным. Он рассказывает о жизни с синдромом «запертого человека». То есть у него был способ общения, который позволил не только разговаривать с медиками, друзьями и семьей, но и написать книгу. Боби сделал это, вообще не прибегая к технике. Но как?

Представьте себя в его положении – очнулись на больничной койке. Как вы могли бы общаться? Как могли бы написать книгу? Только человек с ручкой и бумагой смотрит на вас, готовый записывать слова. Вы из тех, кому повезло, – вы можете моргать одним глазом, но это все. Это единственное движение, которое вам доступно. Значит, разговаривать вы не в состоянии. Однако вы видите и слышите.

Теперь представьте, что вы врач такого пациента и вам необходимо придумать способ общения с ним.

Просто как A, B, C

Вам нужно условиться о способе превратить моргание (все, что доступно пациенту) в буквы. Возможно, сначала вам придет в голову такой вариант: когда он моргнет раз, это будет означать «А», два раза – «В» и так далее. Тогда помощнице останется посчитать, сколько раз моргнул пациент, и записать соответствующие буквы.

Предложив такую идею, мы уже рассуждаем как программисты. То, чем мы занимаемся, лежит в основе вычислительного мышления – это алгоритмическое мышление. Мы придумали серию шагов, которым могут следовать больной и его помощница, чтобы гарантированно передать и понять нужные буквы. В информатике такой способ коммуникации называют алгоритмом. Он представляет собой серию шагов, которые необходимо пройти в заданном порядке, чтобы достичь определенной цели (в данном случае – передать буквы и слова). Алгоритмическое мышление необходимо, чтобы разрабатывать алгоритмы для решения задач.

Красота алгоритмов в том, что им следуют, не имея представления, чтó именно они значат. В случае с нашим алгоритмом помощница предположительно знает, что и для чего она делает, но книга все равно была бы написана, даже если бы она ничего не понимала. Все, что нужно делать, – считать моргания и записывать буквы в соответствии с полученными инструкциями. Мы могли бы дать помощнице таблицу, чтобы сверять по ней буквы, и тогда работа выполнялась бы без какого-либо ее осмысления вообще. Красота алгоритмов заключается в возможности действовать механически, и в этом их смысл – ведь компьютеры тоже слепо выполняют инструкции. Это умеют абсолютно все компьютеры.

Наш алгоритм общения на деле состоит из двух частей. Одну часть выполняет Боби (моргнуть нужное количество раз), а другую – помощница (сосчитать, сколько раз моргнул Боби, и записать соответствующую букву, когда моргание прекратится). Более того, в информатике есть специальное название для алгоритма, при помощи которого делятся между собой информацией два человека или компьютера, – он называется протокол. Если оба человека выполнят свою часть протокола, то слова, которые задумал Боби, окажутся записанными на бумаге. Если кто-то сделает ошибку – например, собьется со счета и таким образом отойдет от протокола, – то сообщение не будет доставлено. В компьютерах хорошо то, что они не делают таких ошибок, каждый раз точно выполняют инструкции. Коль скоро инструкции верны, машины-то уж точно их верно выполнят.

Алгоритмическое мышление – это особый род решения проблем, при котором вы не просто находите один ответ (например, что именно хотел сказать Боби, когда очнулся после инсульта). Вы находите решение в виде шагов, которые могут выполнить другие (в том числе компьютер), – и тоже получить ответ. Мы только что нашли подобное решение для Боби, благодаря которому понимаем не только то, что он пытается сказать в данный момент. Этот способ позволяет нам (и кому угодно) в любой момент выяснить, что он хочет сказать. Но судя по всему, процесс пойдет довольно медленно. Может быть, есть способ получше. Придумывать более удачные, эффективные решения – это тоже часть алгоритмического мышления.

Как это сделал Боби?

У Боби был улучшенный способ, а точнее – алгоритм, который он описывает в своей книге. Вспомним, что у помощницы нет проблем с речью, и это можно использовать. Алгоритм работал так: помощница читала вслух алфавит («А… В… С…»), и, когда звучала нужная буква, Боби моргал. Тогда помощница записывала ее – и опять начинала сначала. Попробуйте это вместе с другом – передайте таким образом свои инициалы. А теперь представьте, что это единственный способ общения с людьми. Остается надеяться, что вас зовут не Яна Яковлевна Яблочкина и не Ярослав Яромирович Якубович!

А теперь представьте, что так проходит вся жизнь. Что так вы вынуждены разговаривать с семьей и друзьями. И если вы хотите, чтобы открыли шторы или переключили телеканал, то придется просить об этом таким способом.

Попробовав, вы, вероятно, осознаете, что для эффективного применения этого метода нужно решить еще кое-какие проблемы. А после нескольких попыток вам, весьма вероятно, придет в голову способ улучшить алгоритм. Что вы можете предложить?

Проверяем детали

Нетрудно осознать, что придется иметь дело не только с буквами алфавита. Нам также понадобятся пробелы, цифры, точки и так далее. Их необходимо добавить к списку букв, который использует помощница. Вероятно, есть способ и получше, чем зачитывать длинный список. Например, сначала задать вопрос: «Это буква?» Если ответ положительный, то будем продолжать как раньше. Если нет, переходим к другим символам. Звучит знакомо? Это та же идея, благодаря которой в компьютерах используются разные наборы символов.

Еще одна проблема, требующая решения: что делать, если человек моргнет по ошибке? У нас должен быть способ сказать: «Проигнорируйте последний раз и начинайте читать буквы с начала». Но так, чтобы не пришлось передавать эту фразу по буквам! Подобным образом, если вы сделали ошибку, нужно найти способ вернуться назад. Нам нужен код, который означает «отменить». Возможность отменить действие – важная часть любого алгоритма с участием людей, так как люди делают ошибки. Например, условимся, что для этого надо быстро моргнуть два раза. Или придумайте что-нибудь получше. Вполне вероятно, что вы обнаружите другие проблемы, требующие решения?

В теории и на практике такая проверка или оценка работы алгоритма является важной составляющей вычислительного мышления. Если мы придумали новый алгоритм, его работу надо очень тщательно проверить. Программисты на оценку программ (то есть алгоритмов для компьютеров) тратят больше времени, чем на их создание. Очень легко ошибиться в какой-то мелочи или забыть о возможной ситуации, с которой должен справиться алгоритм. Но смысл алгоритма в том, что он работает всегда, что бы ни случилось.

Алгоритмическое мышление подразумевает, что мы обдумываем детали и находим решения для возникающих проблем. Мы осознаем, что есть много способов сделать одно и то же, а потом предлагаем улучшенные варианты для конкретной ситуации. Также заметим, что одна из упомянутых выше задач связана с характерной для человека особенностью – свойством ошибаться. Теоретически наше решение работает, надо только моргнуть в нужный момент! И мы могли бы высокомерно заявить, что надо совершать определенные действия, а не получилось – сами виноваты. На практике не всегда моргаешь, когда нужно. И лучше все-таки решить задачу так, чтобы алгоритм работал для людей. В конце концов, мы пытаемся помочь человеку, а не машине! Вычислительное мышление связано еще и с пониманием того, что такое человек.

Улучшаем метод

Что дальше?

Мы могли бы немного ускорить процесс общения для пациента с синдромом «запертого человека», осознав, что порой уже на половине слова можно догадаться, что имеется в виду. Например, если у вас получилось «а-н-т-и-л», с большой долей вероятности можно утверждать, что нужное слово – «антилопа». Значит, поменяем правила так, чтобы помощница высказывала подобные догадки. Кроме того, надо найти способ сказать «нет», если догадка не верна. Например, такое правило: моргнуть, если слово угадано, и не моргать – если нет. Именно по этому принципу работает функция предиктивного ввода текста в телефоне, то есть используется алгоритм для решения очень похожей задачи. То же самое делают поисковые движки, когда вы набираете свой запрос.

Помощники Боби действительно использовали вариант предсказания текста, что и описано в его книге. Он также отмечает, что его очень раздражало, если люди пытались угадать его мысли, не условившись с ним о способе подтверждения. Отсутствие навыков вычислительного мышления у собеседников Боби приводило к тому, что он очень расстраивался, пытаясь «сказать» им, что они ошиблись, а собеседники были уверены, что догадались правильно. Представим, например, что мы продолжаем разговор о животных и я передал буквы «б-а-р-с». Какова будет ваша догадка? Что слово уже закончилось и это слово – «барс»? Нет. Я хотел сказать «барсук».

Возможно, вам тоже пришла идея об угадывании целого слова, ведь вы пользовались предиктивным вводом текста в телефоне. Если так, это значит, что вы только что использовали еще один навык вычислительного мышления – сопоставление с образцом. Часто задачи, в сущности, повторяют то, что вы уже видели в другой ситуации. Если у вас уже есть решение для определенной проблемы, то есть смысл использовать его повторно. Сопоставление с образцом – навык, который позволяет понять, что новая ситуация по сути повторяет уже известную вам, и увидеть, что можно использовать старое решение.

Алгоритмы обеспечивают такого рода общее решение. Мы можем повторно использовать технологию предиктивного ввода текста, потому что у телефона и помощницы Боби одна и та же проблема. Телефон должен догадаться, какие слова набирает по буквам пользователь, а помощница – какое слово передает по буквам пациент с синдромом «запертого человека». Как только мы осознали это сходство, любое решение, найденное для первого случая, реально использовать для второго. Еще лучше, если мы увидим, что обладаем решением, которое подходит для множества разных задач, сделаем описание алгоритма с самого начала и будем использовать его при необходимости. Это называется обобщением алгоритма. Обобщение – очень мощный метод вычислительного мышления.

В самом широком смысле можно считать, что в случае Боби мы занимаемся передачей информации. В любой ситуации, когда есть необходимость передать информацию, используется общий алгоритм. Программисты создают коллекции алгоритмов для разного рода задач, чтобы при необходимости выбрать наиболее подходящий. Например, азбука Морзе тоже алгоритм передачи информации. Используя разную последовательность точек и тире (в нашем случае – долгое или быстрое моргание), обозначают разные буквы. Этот алгоритм изобрели, чтобы передавать сообщения по телеграфу, но, вероятно, получится использовать его и здесь. Мы еще вернемся к этой идее.

В еще более широком смысле мы вправе представить нашу задачу как поиск очередной доли информации (следующая буква). И видимо, мы сумеем обобщить наш алгоритм настолько, что он позволит искать что угодно. Ниже мы вернемся и к этой идее.

В порядке популярности

Боби предложил другой способ улучшить алгоритм АВС. До того, как оказаться на больничной койке, он был главным редактором французского женского журнала Elle и имел хорошее представление о языке. Например, ему было известно, что E – самая распространенная буква (в английском и французском). Поэтому Боби попросил, чтобы буквы зачитывали в порядке их популярности – то есть частотности. В английском этот порядок таков: E, Т, А, О… Во французском, на котором говорил Боби, это Е, S, А, R… Боби, соответственно, использовал французский порядок. Таким образом, помощница быстрее доходила до распространенных букв.

Похожий трюк использовался веками, чтобы расшифровать секретные коды. Он называется частотный анализ. Алгоритм для использования частотности букв был изобретен арабскими учеными около 1000 лет назад. Марию Стюарт обезглавили, потому что сэр Фрэнсис Уолсингем, начальник разведки королевы Елизаветы I, лучше нее владел вычислительным мышлением. Но это уже другая история. Идея Боби использовать частотный анализ – это пример и сопоставления с образцом, и обобщения. Задачи трансформируются, и решения для них используются повторно. Осознав, что расшифровывание кодов и угадывание букв – процессы схожие, мы видим, что частотный анализ, изобретенный для одного, пригоден для другого.

Насколько это быстро?

Давайте вернемся к алгоритму Боби, который мы определенно усовершенствовали. Новый способ должен быть лучше изначальной идеи – моргать разное количество раз для разных букв. Однако напрашивается вопрос: как быстро это будет – сколько времени уйдет, чтобы написать книгу? Удалось ли найти наилучший способ или можно предложить более быстрый алгоритм, который облегчит написание книги?

Нам необходимо определить эффективность алгоритма. Проведем эксперимент и применим научное мышление. Например, следующим образом: несколько раз определим время, которое уходит на передачу какого-то отрывка с каждым алгоритмом и с разными участниками, и выясним, в каком случае все было в среднем быстрее. Однако на это уйдет очень много времени и сил. Есть способ и лучше.

Можно прибегнуть к аналитическому мышлению. В этом случае необходимо сделать простые вычисления. Например, давайте учитывать не время, а сделанную работу. Если подсчитать, сколько букв алфавита произносит помощница, то мы всегда определим потраченное время. Просто надо знать, сколько времени уходит на произнесение одной буквы, и умножить это время на количество букв. Мы только что произвели действие, которое называется абстрагированием. Это еще один элемент вычислительного мышления, который применяется, чтобы упростить задачи и облегчить написание программ. Абстрагирование – просто длинное слово, которое подразумевает, что некоторые подробности скрывают или игнорируют. Мы проигнорировали такую деталь, как точное время, потраченное на всю книгу, и вместо этого подсчитали произнесенные буквы. «Число произнесенных букв» – это абстракция реально потраченного времени. Такой принцип очень часто используется в вычислительных процессах, чтобы упростить их работу.

Как же нам выяснить, сколько букв надо произнести? Для этого нужно задать несколько вопросов. Самый простой звучит так: сколько это будет в лучшем случае? Каково минимальное количество букв, которое должна произнести помощница, чтобы получилась книга? Рассмотрим и худший случай. Если не повезет, то насколько? Наконец, рассмотрим средний вариант и таким образом получим реалистичную оценку необходимой работы. Давайте чисто теоретически представим, что нам нужны только буквы алфавита, без цифр и знаков пунктуации. И проанализируем наш простой алгоритм, в соответствии с которым помощница говорит: «A, B, C…»

В лучшем случае вся книга будет состоять только из «А»: «АААА…» (возможно, выражая боль автора). Чтобы общаться при помощи одной буквы «А», достаточно сказать «А» один раз (ответить на один вопрос), и ответ будет получен. Здесь мы снова используем абстракцию – сначала анализируем, что будет, если посчитать только одну букву, и игнорируем всю книгу – по крайней мере для начала. Умножьте наш ответ для одной буквы на количество букв в книге и получите упомянутый лучший случай.

В худшем случае (для латинского алфавита), при котором кто-нибудь, например, все время жужжит («ZZZZ…»), потребуется 26 вопросов для каждой буквы. Итак, мы определили границы, в которых будет происходить передача любой информации. У нас никогда не получится лучше, чем при варианте с одной буквой, и хуже, чем со всеми 26.

Оценка будет точнее, если учесть среднее количество вопросов на каждую букву, то есть средний случай. Сделать это не так трудно. В длинном сообщении на каждую «А» где-нибудь еще придется «Z», на каждую «B» найдется «Y» и так далее. Это значит, что в среднем во всей книге на каждую продиктованную букву надо будет задать 13 вопросов. Умножьте число букв в книге на 13, и вы получите примерную оценку работы при ее написании. Умножьте это на среднее время, которое уходит у помощницы, чтобы произнести букву, и вы получите время, необходимое, чтобы написать книгу.

Отметим, что мы снова оцениваем наш алгоритм – но на сей раз нас интересует не то, действует ли он вообще, а то, насколько быстро он действует. У алгоритма оценивают много разных аспектов, но надежность и эффективность – два важнейших для оценки.

Изменение, внесенное Боби, — сначала спрашивать о распространенных буквах — улучшает ситуацию. Вероятно, получится уложиться в 10‒11 произносимых букв. А с учетом частотности, мы рассчитаем это точнее. Частотность можно уточнить или определить самостоятельно. Возьмите отрывок из любимой книги и посчитайте, сколько раз появляется каждая буква. Потом расположите буквы по порядку, начиная с самой распространенной, и посчитайте вероятность их появления. Средний случай — это число букв, которое необходимо произнести для угадывания одной буквы, вероятность появления которой равна 50%.

Итак, частотный анализ привел к улучшениям, но не слишком значительным, и в худшем случае для выяснения одной буквы все равно надо задать 26 вопросов. Но каждый специалист по информатике знает, что можно существенно улучшить этот процесс. Любая буква выясняется всего за пять вопросов! Гарантированно! И это не средний случай, а худший! Знаете, какие пять вопросов надо задать?

20 вопросов?

Уложитесь в пять

Смогли вы ответить на этот вопрос или нет, я гарантирую, что вы знаете, о каких вопросах идет речь. Чтобы вспомнить о них, нужно рассмотреть другую задачу.

Давайте сыграем в игру «20 вопросов». Это детская игра, в которой водящий задумывает известного человека, а вы пытаетесь догадаться, кто это, задавая вопросы. Изюминка в том, что отвечать следует только «да» или «нет». Сыграйте в эту игру с другом и обратите внимание, какие вопросы вы задаете. Представим, как может пойти игра.

«Вы женщина?» — «Нет».

«Вы живы?» — «Нет».

«Вы были кинозвездой?» — «Нет».

«Вы жили в Британии?» — «Да».

«Вы были писателем?» — «Да».

«Вы жили в XX веке?» — «Нет».

«Вы жили в XIX веке?» — «Нет».

«Вы Шекспир?» — «Да».

Вероятно, играя, вы задавали похожие вопросы. Очень маловероятно, что вы сразу начали спрашивать: «Вы Аристотель? Вы Джеймс Бонд? Вы Мария Кюри?» Так вы никогда бы не нашли ответ за 20 вопросов. До подобных формулировок дело обычно доходит в конце, когда вы практически уверены, что знаете, кто это (как мы только что показали). Скорее, вы начали с вопроса вроде «Вы женщина?».

Почему это хороший вопрос для начала? Да потому, что он отметает половину возможных вариантов при любом ответе. Если вы спросите «Вы королева Англии?», то в случае успеха отбросите миллионы других вариантов, а в случае (более вероятного) неуспеха — только одного человека. Чтобы сразу угадать, вам должно повезти не меньше, чем выигравшему в лотерею. Значит, секрет игры «20 вопросов» — задавать вопросы так, чтобы каждый раз отбрасывать половину людей, каким бы ни был ответ.

Насколько это эффективно?

Задавать вопросы, которые оставляют половину возможных ответов, — лучше, чем называть конкретное имя, но насколько? Давайте предположим, что я изначально задумал кого-то одного из миллиона. Если после каждого вопроса отметать половину людей, сколько вопросов понадобится? После первого останется 500 000 человек, после второго — 250 000... После десяти вопросов от исходного миллиона останется примерно 1000 человек (рис. 1). Продолжаем... После следующего вопроса осталось 500, потом 250, 125... и на двадцатом вопросе остается один возможный человек. Если вам удастся каждый раз точно задавать вопрос, после которого останется половина ответов, то вы гарантированно выиграете. И всегда это будет 20 вопросов.

Все это, конечно, алгоритмическое мышление. Мы пытались разработать алгоритм для игры «20 вопросов». Однако до конца решить задачу не удалось — было непонятно, как определить нужные вопросы. Это остается вашей задачей во время игры. Здесь используется еще один трюк вычислительного мышления — декомпозиция (разложение на части). Надо разделить проблему на части, чтобы сосредоточиться на каждой отдельно. Пока у нас получилось найти общую стратегию. Подобрать конкретные вопросы, которые оставят половину вариантов, — отдельная проблема.

Декомпозиция — популярная стратегия для решения задач и жизненно важный инструмент информатики. Задачи, которые надо решать при составлении программ или разработке процессов (например, для вашего ноутбука или телефона), имеют гигантские масштабы. Современные компьютерные микросхемы сложнее, чем дорожная сеть всей планеты Земля. Представьте, что вы пытаетесь решить такую задачу в один прием. Это можно сделать, только разложив ее на части и работая над ними отдельно.

Декомпозиция полагается на абстракцию — сокрытие деталей. Здесь мы абстрагируемся от конкретных вопросов и думаем только о том, какого типа вопросы надо задавать. Мы также использовали декомпозицию, когда размышляли, насколько эффективным был наш изначальный алгоритм. Чтобы выяснить, каким образом можно написать книгу, мы разложили одну задачу на две: выяснить, как передавать отдельные буквы, и провести всю необходимую работу с помощью полученного решения.

Новый алгоритм

Итак, если правильно задавать вопросы, то в худшем случае понадобится только 20 вопросов, чтобы угадать задуманного человека из миллиона возможных вариантов. Вспомним теперь, что хватит 13 вопросов (в худшем случае — 26), чтобы определить одну из 26 букв алфавита. «Да/нет» не отличается от «моргнуть / не моргать». А спрашивать «Это A? Это В?» — примерно то же самое, что спрашивать «Вы Микки-Маус?» или «Вы Нельсон Мандела?». Вы точно так же пытаетесь выяснить, о какой из многих вещей я думаю. Это опять-таки та же самая задача, что и предиктивная система набора текста в телефонных сообщениях!

Но если это та же самая задача, то и соответствующая ей стратегия должна обеспечить нам более удачное решение, чем уже найденное. Здесь мы снова используем сопоставление с образцом и обобщение. Мы преображаем задачу, чтобы повторно использовать решения. Каков эквивалент решения, которое оставит только половину вариантов, применительно к алфавиту? Сначала, наверное, имеет смысл спросить: «Это гласная?» — но как будут выглядеть остальные четыре вопроса? Каждый раз оставлять только половину вариантов из алфавита? Напрашивается такой первый вопрос: «Это между А и М?» Если ответ утвердительный, то потом мы спрашиваем: «Это между А и F?» Если ответ отрицательный, мы спрашиваем: «Это между N и S?» — и так далее. Таким образом мы гарантированно доберемся до любой буквы алфавита, которую задумал человек, всего за пять вопросов, как это показывает дерево решений на рис. 2. Начните сверху диаграммы и двигайтесь вниз в соответствии с ответами «да/нет».

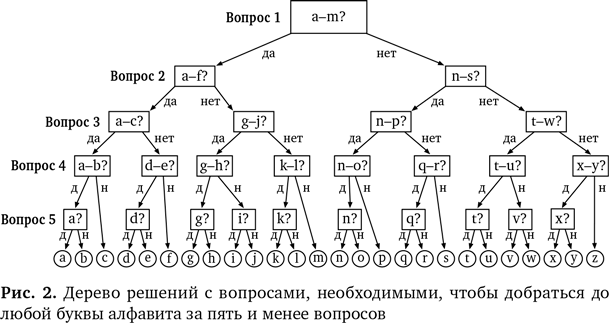
В этот момент нужно подключить еще один компонент алгоритмического мышления. Необходимо прояснить все детали, потому что здесь можно запутаться. Спрашивая «Это между А и М?», надо уточнить, входит ли «М» в этот промежуток (входит).

Попробуем еще больше усовершенствовать эту технику, используя частотный анализ. Поскольку букв только 26, реально добраться до «Е» и других распространенных букв быстрее чем за пять вопросов. Попробуйте сделать дерево решений, которое это обеспечит. Кроме того, можно использовать принцип предиктивного набора текста, чтобы предугадывать набранные не до конца слова. Все подобные решения из более ранних алгоритмов применимы и здесь. Мы повторно используем готовые решения.

Коды для букв

Дерево решений представляет собой совсем другой подход. Если мы примем «да» и «нет» или «моргнуть» и «не моргать» за 1 и 0, тогда дерево решений определит двоичную последовательность, которую должен усвоить больной с синдромом «запертого человека», чтобы обозначить каждую букву (рис. 3).

Таким образом, чтобы ускорить процесс, можно отказаться от вопросов. Человек, передающий информацию, проходит определенную последовательность для каждой буквы, а другой человек — записывает. Таким образом, обозначая морганием код 0110 (не моргать, моргнуть, моргнуть, не моргать), выражаем букву «P». Соответственно, дерево решений преображаем в таблицу поиска, как на рис. 4. Тому, кто хочет общаться с больным, можно дать либо дерево решений, либо такую таблицу. В сущности, мы только что изобрели код для общения, похожий на азбуку Морзе. И снова очевидно, что наша задача, в сущности, аналогична той, которую пытался решить Сэмюэл Морзе, чтобы передавать информацию с помощью телеграфа. Точки и тире соответствуют нашем единицам и нулям или вариантам «морг­нуть» и «не моргнуть». И снова мы применяем обобщение.

Однако не стоит выбирать решение второпях. Детали играют большую роль. Если не задавать вопросов, как узнать, что человек передает информацию? Если он не моргает, что это значит — он уснул или просто ничего не говорит? Как узнать, что он начал передавать буквы? Сколько времени продолжается «неморгание»? Небольшое изменение привело к необходимости решить много новых проблем. Сэмюэл Морзе их решил. В азбуке Морзе с этой целью используются три символа, а не два: точки, тире и тишина. Продолжительность каждого элемента точно определена. Какой бы долгой ни была точка, пауза между точками и тире одинаковая. Между буквами она в три раза дольше точки, между словами — в семь раз. Это обеспечивает структуру, которую мы потеряли, отказавшись от вопросов.

Решение в виде кода отлично подошло для телеграфа, и его вариант лежит в основе взаимодействия компьютеров в сети. Но можно ли сказать, что это решение больше подходит человеку с синдромом «запертого человека», — вопрос спорный. Машинам легко иметь дело с точными промежутками времени, а людям это гораздо сложнее, чем просто задать вопрос.

Выбираем лучшее решение

Алгоритмы поиска

Наше решение для игры «20 вопросов» можно использовать, чтобы помочь пациенту с синдромом «запертого человека» разговаривать, потому что задача, в сущности, не меняется. Это задача поиска: у нас есть серия предметов и надо найти один конкретный. Решения для этой задачи называются алгоритмами поиска, и они обеспечивают беспроигрышный способ что-нибудь найти. Первый подход, проверка всех вариантов по очереди («Это A?», «Это B?..», «Это певица Адель?», «Это Джеймс Бонд?..»), — алгоритм под названием линейный поиск. Порой это лучшее, что есть в вашем распоряжении. Например, если вы были свидетелем ограбления и участвуете в опознании преступника из нескольких людей, линейный поиск будет для вас оптимальным: рассмотрите по очереди каждое лицо, пока не увидите в ряду человека, который совершил преступление. Линейный поиск хорошо работает и тогда, когда вещи, среди которых вы ведете поиск, никак не упорядочены. Если вы ищете носок, который может быть в любом ящике комода, начните сверху и последовательно проверяйте ящики один за другим.

Другой алгоритм включает вопросы, после ответа на которые остается половина вариантов: «Эта буква стоит раньше N?», «Это женщина?». Найти подобные вопросы — общая стратегия решения задач под названием «разделяй и властвуй». Если вы найдете такое решение, ответ, вероятно, будет получен очень быстро. Почему? Потому что, как мы видели, если несколько раз сократить число вероятных ответов вполовину, можно очень быстро прийти к одному варианту — гораздо быстрее, чем если бы мы проверяли последовательно пункт за пунктом. Заметим, что здесь мы снова используем обобщение. Самый простой алгоритм поиска по принципу «разделяй и властвуй» называется бинарным поиском. Представьте, что все предметы, среди которых вы ищете нужный, стоят по порядку и самый маленький — на одном конце, а самый большой — на другом. В ходе бинарного поиска вы подходите к предмету, который расположен посередине, и проверяете, лежит ли нужная вам вещь до или после него. Затем вы отбрасываете ненужную половину и повторяете ту же операцию с оставшейся. Вы делаете это до тех пор, пока не остается один предмет — тот, который вы ищете. Возможно, примерно так вы поступаете, когда нужно найти фамилию в толстом телефонном справочнике. Конечно, вы не будете начинать с первой страницы и проверять каждое имя по очереди, пока не найдете нужное!

Кроме этих двух, есть еще много алгоритмов поиска. Например, каким образом поисковая система вроде Google просматривает каждую веб-страницу на планете за доли секунды? Она использует еще более продвинутый алгоритм!

Чтобы применить алгоритм поиска, необходимо задействовать абстрагирование. Мы абстрагируемся от деталей конкретной задачи и смотрим, нельзя ли свести ее к задаче поиска, и тогда наш алгоритм поиска становится готовым решением для многих задач. Можно подойти к этому с другой стороны: как только мы придумаем стратегию выигрыша за 20 вопросов, то сумеем обобщить это решение до алгоритма «разделяй и властвуй» — у нас есть общая стратегия, которая работает и для других задач. Абстрагирование и обобщение часто неразрывно связаны.

Делаем жизнь Боби лучше

Значит, надо было устроить так, чтобы помощница задавала Боби вопросы, после которых исключалась бы половина из возможных вариантов. Представьте себе: придется задать в худшем случае пять вопросов вместо 13 в среднем, помноженные на все количество букв в книге. И речь идет не только о книге, но и о разговорах с друзьями и родственниками, докторами и медсестрами. Если бы он был немного знаком с информатикой, насколько легче могла бы стать его жизнь!

Главное — алгоритмическое мышление

Здесь стоит отметить, что пока мы вообще не учитывали технологии. Речь шла исключительно о двух «беседующих» людях. Теперь, когда у нас есть хороший способ, то есть хороший алгоритм, озаботимся тем, как его автоматизировать при помощи подходящих технических средств. Мы могли бы использовать систему управления с помощью движения глаз, которая распознает моргание, или шапочку с электродами, которая улавливает, «да» у человека в мыслях или «нет». Но дело в том, что, какую бы технику мы ни использовали, ей все равно потребуется алгоритм поиска. Если выбрать его неверно, то при всех ее преимуществах общение все равно пойдет медленно — придется задавать 13 вопросов вместо пяти. И нет никакой разницы, будет ли помощником компьютер или человек. Если сначала не продумать алгоритм, система может оказаться мучительно медленной. Вычислительная техника — это не только технологии. Это и вычислительное мышление, которое необходимо, чтобы найти хорошее решение.

Еще важнее — понять человека

Итак, нет сомнений, что жизнь Боби могла бы стать лучше, если бы вычислительное мышление применялось активнее. Но не будем торопиться с выводами. Возможно, мы неправильно поняли ситуацию. Есть вероятность, что в этом случае он никогда бы не написал книгу и его жизнь превратилась бы в еще больший ад. Почему? Мы начали не с технологий, а с информатики. Возможно, надо было начинать с человека. Удалось ли нам учесть главное?

В качестве показателя успеха, или нашей абстракции, мы использовали количество заданных вопросов. Задавать вопросы — задача помощницы, и это нетрудная работа, хотя и нудная. А что, если Боби было трудно моргать? При его решении надо было моргать один раз на каждую букву. Наш алгоритм типа «разделяй и властвуй» требует, чтобы он моргал пять раз. Умножьте это на всю книгу. Не исключено, что наше решение сделало бы его задачу в пять раз сложнее! Но возможно, моргать было легко и наш алгоритм действительно лучше. Мы не знаем ответа, потому что не задали вопрос. А стоило бы сначала спросить. Боби не рассказал об этом в книге, и у каждого может быть свой ответ на этот вопрос. Поэтому и надо начинать с человека.

Более того, решение Боби понятно любому. Наше же относится к более сложным и, вероятно, потребует объяснений. И объяснять этот метод будет не Боби. Думать о людях — это важно.

Описанная ситуация выдвигает на первый план еще один необходимый аспект оценки алгоритма. Мы должны ответить на вопрос: легко ли использовать наш алгоритм, не делая ошибок, и останутся ли у людей хорошие впечатления? Это необходимо сделать, даже если алгоритм выполняет компьютер, а люди взаимодействуют с программой. Так мы учитываем удобство использования и восприятие пользователем алгоритма. Подобная оценка в конечном итоге должна включать тестирование решений с участием реальных людей. И чем быстрее это делается, тем лучше.

Ему подошло

Про решение Боби одно известно точно: оно подошло для его целей. В конце концов, так он написал целую книгу. Возможно, помощница не только записывала его слова, но и открывала шторы, разговаривала с ним об окружающем мире или просто давала немного человеческого тепла. Возможно, вся книга нужна была для того, чтобы у Боби был постоянный собеседник, который получал за общение с ним деньги от издательства!

Таким образом, важно не только то, что коммуникационный алгоритм послужил созданию книги. Сама книга помогла удовлетворить глубинную потребность в непосредственном общении с другим человеком. Если бы человека заменили техникой, то Боби лишился бы того единственного, что поддерживало в нем жизнь.

В то же время, возможно, если бы он мог говорить с компьютером, то попал бы с больничной кровати в виртуальный мир и стал бы посылать сообщения друзьям, пользоваться социальными сетями, управлять аватаром, а однажды — даже версией себя в виде робота, который передвигается в реальном мире… Возможно, все это улучшило бы ситуацию.

Значит, прежде всего необходимо определить, чего на самом деле хочет человек и в чем он нуждается в первую очередь. В ситуации, когда удобство метода обретает крайне большое значение, надо все устроить так, чтобы пользователь с самого начала активно участвовал в процессе. Мы называем это разработкой, ориентированной на пользователя. Одна из ее самых мощных разновидностей называется проектированием с участием пользователя: конечный пользователь помогает найти идеи для разработки, а не просто участвует в их оценке. Именно это, в сущности, сделал Боби — он непосредственно участвовал в разработке способа коммуникации. На деле ориентированное на пользователя проектирование предпочтительнее при разработке любой системы, предназначенной для людей, а не только в экстремальных случаях. Именно пользователям в конечном итоге придется адаптировать доступные инструменты так, чтобы те подошли для их целей — и не только с технической точки зрения, но и с эмоциональной и социальной. В противном случае можно получить «решение», которое будет замечательным в теории, но на практике обернется адом. Поэтому программистам приходится думать не только о компьютерах, но и о многих других вещах.

Глава 3
Магия и алгоритмы

Искусному фокуснику, который сам придумывает магические трюки, и опытному программисту нужны одни и те же навыки, а именно вычислительное мышление. Фокусы — это алгоритмы, и компьютерные программы — тоже. Оказывается, чтобы осуществить поиск данных, первые компьютеры воспроизводили фокус под названием «Сон об австралийском маге». Программисты, несомненно, настоящие волшебники!

«Сон об австралийском маге»

Механизм предсказания будущего

В фокусе под названием «Сон об австралийском маге» иллюзионист предсказывает, какая карта останется в конце, хотя точно это не может быть известно заранее. В основе фокуса — информатика. Показывают его следующим образом.

Перед началом представления возьмите обычную перетасованную колоду карт рубашкой вверх и поместите восьмерку червей 16-й сверху. На 32-е место поместите какую-нибудь запоминающуюся карту, например туза червей. Положите колоду на стол рубашкой вверх. Теперь возьмите восьмерку червей из другой колоды (для дополнительного эффекта лучше использовать карты большого размера) и поместите ее в запечатанный конверт. Положите конверт под стол так, чтобы он оставался на виду с начала и до конца фокуса.

Перейдем к тому, что видит аудитория. Вызовите добровольца. Распределите карты в одну линию на столе лицом вверх, чтобы зрители видели, что это обычная перетасованная колода. Объявите, что сначала вам нужно поделить колоду примерно пополам. Попросите добровольца выбрать любую карту примерно посередине и покажите руками, что вы имеете в виду. Вы обязательно должны сделать так, чтобы ваши руки оказались над 16-й и 32-й картами. Таким образом вы ненавязчиво ограничиваете выбор до какого-то варианта между ними. Сбросьте карты справа от той, которую укажет доброволец (нижнюю часть колоды), и попросите его подтвердить, что это был свободный выбор. Возьмите оставшиеся карты и, держа их рубашкой вниз, объясните, что ночью перед выступлением вам всегда снятся странные сны, в которых маги учат вас новым фокусам. Накануне во сне к вам явился австралийский маг и научил методу «шиворот-навыворот», позволяющему угадывать карту, о которой никак нельзя было знать заранее.

Теперь сдавайте карты, по очереди раскладывая их в две кучки. Делая это, говорите «шиворот», когда кладете карты рубашкой вверх в первую стопку, и «навыворот», когда кладете карты лицом вверх во вторую стопку. Как только все карты будут выложены, сбросьте «шиворот» и отметьте, что вы всегда сбрасываете эту стопку. Возьмите стопку «навыворот», поверните ее рубашкой вверх и повторяйте процесс, каждый раз сбрасывая «шиворот». Продолжайте, пока у вас не останется одна карта из стопки «навыворот», лежащая лицом вверх. Это будет восьмерка червей. Скажите зрителям, что это и есть искомая карта. Попросите добровольца подтвердить, что он не знал заранее, какая карта останется в конце, а также показать и назвать полученную карту. Также попросите его подтвердить, что он разделил колоду исключительно по своему усмотрению. Переверните первые несколько карт в сброшенной стопке и скажите: «Если бы вы сдвинулись даже на одну карту, результат был бы другой».

Теперь укажите вот на какую странную вещь: в вашем сне австралийский маг сказал, что нужно заранее положить в конверт одну конкретную карту. Попросите добровольца посмотреть под столом и достать из конверта карту, предсказанную австралийским магом в вашем сне. Это тоже восьмерка червей!

Поблагодарите добровольца и попросите аудиторию поаплодировать ему.

Хитрые алгоритмы

Какое отношение фокус имеет к информатике? Здесь мы имеем так называемый самовоспроизводящийся фокус — именно это в информатике называют алгоритмом. Под алгоритмом подразу­ме­вается серия инструкций, которая всегда приводит к конкретному желаемому эффекту, если следовать им в заданном порядке. В данном случае — магический эффект: у вас остается именно предсказанная карта. Компьютерные программы — всего лишь алгоритмы, написанные на языке, который скорее поймет компьютер, чем фокусник. С их помощью программист добивается, чтобы программа выполняла задуманные им действия.

Алгоритм, лежащий в основе «Сна об австралийском маге», показан на рис. 5.

Этот конкретный алгоритм содержит не только шаги, которые надо выполнять последовательно. В нем есть циклы, например «повторите 4 раза». Цикл показывает, что некоторые инструкции надо повторить. Он позволяет не писать одно и то же много раз. Именно такие инструкции программисты используют в компьютерных программах, чтобы компьютер повторил какие-то указания. Есть и второй цикл: «Повторите, пока не останется карт». Этот цикл воспроизводится 4 раза, как указано в первом цикле. Каждый раз вы проходите через всю колоду, оставляя и сбрасывая карты, пока не останется ни одной.

Придумываем фокусы

Чтобы придумать новый трюк, фокусник должен использовать тот же тип мышления, что и ученый-информатик, — а именно вычислительное мышление. Карточный фокус подразумевает вычисления, только они проводятся с помощью колоды карт вместо компьютера. Чтобы изобрести новый фокус, необходимо алгоритмическое мышление. Фокусник должен продумать серию шагов, которые можно повторить и обязательно получить магический эффект. Ему абсолютно необходимо, чтобы фокус получался всегда. Он не хочет глупо выглядеть на сцене, и поэтому нужно продумать все до мельчайших деталей. Необходимо удостовериться, что шаги должны делаться именно в указанной последовательности. Как и в программировании, нужно продумать каждый возможный вариант. Может ли доброволец как-то помешать выполнению фокуса? Если да, нужно знать, что делать в этом случае. Кроме того, следует достаточно точно записать все действия, чтобы в будущем сам фокусник или кто-то другой смог повторить их и успешно показать фокус (хотя маги, в отличие от ученых-информатиков, не склонны раскрывать свои секреты!). Все это — алгоритмическое мышление в действии.

Главное здесь в том, что, как только маг изобрел свой трюк и записал алгоритм (возможно, рунами!), всякий, кто знает этот алгоритм, в состоянии показать фокус. Для этого не придется ничего изобретать. Надо просто четко следовать инструкциям. Ученик чародея может показать фокус, даже если ему абсолютно не понятно, как он работает. Правильно и точно выполните необходимые действия — и получите задуманный волшебный эффект.

Почему это важно для информатики? Именно так мы добиваемся, чтобы работал компьютер. Компьютеры — это куски металла и кремния. Они не понимают, что делают. Просто слепо следуют инструкциям, как ученик колдуна. Программисты делают всю творческую работу, составляя инструкции. Для программирования важен навык писать инструкции очень точно и недвусмысленно, чтобы не допустить несоответствий. Цель каждой инструкции не должна вызывать никаких сомнений: компьютер должен в точности следовать указаниям. Каждый возможный исход событий должен быть описан в инструкции — компьютер не справится с непредвиденным. Однако, следуя этим указаниям, компьютер может творить чудеса (и даже казаться разумным, как мы увидим далее).

Все электронные устройства, которые вы когда-либо видели в действии, слепо следуют алгоритму.

Делим на части

Чтобы придумать фокус, например можно составить его из частей, отдельно поработав над каждым шагом и его представлением. Здесь мы снова наблюдаем вычислительное мышление в действии, а именно — декомпозицию. Фокус «Сон об австралийском маге» состоит из четырех основных шагов. Во-первых, нужно подготовить колоду, поместив карты на известные позиции. Во-вторых, нужно сбросить нижнюю часть колоды, создав у добровольца ощущение, что он сам выбирает, как ее поделить, от чего зависит результат (хотя это не так). Следующий шаг — раскладывать карты так, чтобы в итоге осталась одна. И последний шаг — раскрыть предсказание. Если мы запишем фокус в виде алгоритма на этом уровне детализации, то получим что-то вроде изображенного на рис. 6а.

Обратите внимание, что здесь мы прибегли к абстрагированию, то есть прячем детали. В этом описании мы скрыли, как выполняются шаги. Эти детали можно записать в виде отдельного мини-алгоритма. Например, алгоритм для шага, когда мы сбрасываем каждую вторую карту, как показано на рис. 6b.

На самом деле мы уже занимались такого рода абстрагированием для каждого из шагов в начальной версии алгоритма. Зачем? Чтобы вы увидели общую идею и не увязли в подробностях.

Такого рода декомпозиция значительно упрощает понимание алгоритма. Обращать внимание на детали нужно, только если (или когда) необходимо понять, как их повторить, а не для чего они нужны. Если вы хотите иметь шпаргалку, которая поможет вам запомнить шаги (напишите ее на тыльной стороне кисти), то используйте упрощенную абстрагированную версию. Все детали записывать не нужно, ведь вы не сможете это прочитать. Вероятно, стоит записать одну деталь или один шаг, которые вы все время забываете. Декомпозиция поможет сделать все правильно.

Разложив один фокус на отдельные части, вы можете использовать их элементы в других фокусах. Например, во многих фокусах открывают что-то предсказанное заранее. Можно положить предсказание в конверт и оставить его у всех на виду, как это сделали мы. Однако есть и другие способы. Например, записать видеоролик, в котором ваш друг будет держать предсказанную карту, и показать его. В этом, в частности, и состоит прелесть декомпозиции. Необязательно использовать решение целиком — можно повторно использовать (и обобщить) лишь какие-то его части. Например, когда понадобится что-нибудь «раскрыть», можно использовать описанное решение.

Декомпозиция также позволяет заменить отдельные части алгоритма новыми вариантами — другими способами сделать то же самое. Например, представим, что в «Сне об австралийском маге» мы кладем предсказание в воздушный шар и украшаем им сцену. Это не более чем альтернативный способ сделать шаг 4 — но более эффектный! Детали для алгоритма раскрытия карты в варианте с воздушным шаром следует проработать и включить в инструкции, не меняя алгоритм верхнего уровня.

Конечно же, придется изменить два шага — подготовку и собственно раскрытие. Одно не сделать без другого. Однако другие части фокуса можно и вовсе не менять. Программисты пишут программы именно так, составляя их из множества самодостаточных частей.

Всегда ли получается фокус?

Этот фокус получается потому, что, если несколько раз сбросить каждую вторую карту, у вас обязательно останется 16-я. Но гарантировано ли это? Достаточно ли вы доверяете мне, чтобы повторить этот фокус на сцене, удовлетворившись только моими заверениями о том, что он получается всегда? Или вы хотите получить какие-то доказательства? В науке никогда не доверяют голословным заявлениям, но требуют неопровержимые доказательства! Поэтому нам нужно оценить алгоритм, чтобы проверить, действительно ли он работает без сбоев.

Но как в этом убедиться? Например, можно повторить фокус много раз подряд. Если будет получаться каждый раз, мы приобретем некоторую уверенность в успехе. Программисты называют этот процесс тестированием. Чем больше тестов проведешь, тем увереннее будешь. Но как мы гарантируем, что в следующий раз, когда мы будем показывать фокус зрителям, не возникнет тот единственный случай, когда алгоритм не сработает? Реально ли протестировать все возможности? Для этого необходимо проверить все возможные варианты расположения карт в колоде перед началом фокуса. В каждом случае нужно убедиться, что фокус получается, в каком бы месте доброволец ни разделил колоду. Однако все эти варианты нереально проверить на практике.

Если вместо этого подключить логическое мышление, проводить тестирование не придется. В первую очередь надо отметить, что достоинство карт, за исключением 16-й, не играет абсолютно никакой роли. Они могут быть пустыми, и в этом случае логика, объясняющая фокус, не изменится. Конечно, он будет выглядеть не так волшебно, но сейчас речь не об этом. Мы не будем показывать фокус с ненастоящими картами — просто это допущение помогает нам думать. Оно означает, что в наших рассуждениях мы учитываем не достоинство карт, а их положение в колоде. Мы (еще раз) обращаемся к абстрагированию — опускаем некоторые детали (на этот раз — достоинство карт), чтобы нам было проще рассуждать.

Это уменьшает объем необходимых тестов. Нам просто нужно проверить, получается ли фокус вне зависимости от того, как мы делим колоду. Останется ли у нас 16-я карта, независимо от того, куда укажет доброволец? Колоду можно разделить только в 52 местах, поэтому теперь мы знаем, что достаточно проверить 52 случая и посмотреть, всегда ли остается 16-я карта. Возможно, к этому моменту вы уже поняли, что это не всегда срабатывает! Необходимо ограничить промежуток, в рамках которого можно делить колоду…

Программисты сталкиваются с похожей проблемой при тестировании программ. Невозможно учесть все, что теоретически может сделать пользователь с программой. Поэтому они применяют логическое мышление, чтобы разработать план тестирования: ряд тестов, которые при положительном исходе дадут высокую (хотя и не полную) гарантию правильной работы программы.

Пятьдесят два варианта — это слишком много, а программисты (в отличие от фокусников) по натуре ленивы. Зачем делать больше работы, чем необходимо? Давайте лучше еще порассуждаем. Давайте сделаем упрощенную схему колоды и посмотрим, что получится, если сбрасывать каждую вторую карту. Такого рода вычислительное моделирование является важной частью вычислительного мышления. В нашей модели каждую карту представляет ее позиция в начале фокуса. Мы используем «...», чтобы показать, продолжается ли ряд чисел (снова абстракция). Вот наша модель колоды:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 …

Что останется, если мы сбросим каждую вторую карту, начиная с первой? Только четные позиции, а это означает, что 16-я карта останется на месте:

2 4 6 8 10 12 14 16 18 …

Мы снова сбрасываем каждую вторую карту, и остаются следующие позиции:

4 8 12 16 …

а потом

8 16

и, наконец,

16.

Эта модель показывает, что как при большем, так и при меньшем числе карт происходит одно и то же. Очевидно, что 16-я карта остается в любом случае, если убирать каждую вторую.

Однако у нас остается проблема, связанная с «…». Здесь мы наблюдаем важное свойство абстрагирования. Если отбросить важную деталь, то мы, вероятно, получим неправильный ответ. Логическое мышление тоже с легкостью заведет вас не туда, если не продумать в точности все возможные варианты. Если бы в начале фокуса мы разделили колоду в какой-то точке до 16-й карты, то, конечно, эта карта ушла бы при первом разделении. Тогда у нас осталась бы другая карта, например восьмая. Возможно, вы поняли это, как только обратились к абстрагированию. Однако есть еще одна похожая, но немного более тонкая проблема. Давайте снова проведем моделирование, но увеличим масштаб. Результат показан на рис. 7.

Ну и ну. Если взять 32 карты или больше, у нас останется не 16-я карта, а 32-я. Таким образом, даже если мы добьемся того, что 16-я карта не будет сброшена в начале, фокус не сработает, если не подготовиться заранее. Нам нужно добавить еще одно условие. Как показали логические рассуждения, колоду необходимо разделить в каком-то месте после 16-й и перед 32-й картой. Поэтому важно сказать добровольцу, что нужно отбросить «примерно половину». Однако на самом деле подразу­мевается не примерное разделение, а весьма точное — «между 16-й и 32-й картой». Вот почему нужно ограничить руками пространство над 16-й и 32-й картами, чтобы сориентировать добровольца при делении колоды. Это делается для того, чтобы условие, или, как выразился бы программист, входное условие, было выполнено без ведома добровольца.

Итак, мы использовали численное моделирование и логическое мышление и таким образом убедились, что фокус действительно работает, но при условии, что перед тем, как мы начинаем сбрасывать карты, их в колоде минимум 16 и максимум 31. Численное моделирование — это создание моделей вычислительных процессов с целью их изучения. Здесь мы прибегли к моделированию, чтобы посмотреть, всегда ли получается фокус, но подобным образом можно провести и обобщение. Наша модель показывает принцип, лежащий в основе фокуса. Главное в нем — не игральные карты. Мы абстрагировались от них, как и от многих других деталей. Выявив этот базовый принцип, мы можем придумать другие варианты фокуса, основанные на нем. Мы еще вернемся к этому позже.

Перфокарты

Магия успешного поиска

Наш фокус имеет с вычислительными алгоритмами связь более глубокую, чем то, что и фокус, и программы являются алгоритмами. Вариант алгоритма фокуса применялся в ранних компьютерах для поиска по данным, записанным на перфокарты. Перфокарты — это физически существующие карты, которые использовали в качестве долгосрочной памяти, чтобы хранить данные для последующей обработки.

Информацию записывали на перфокарты, пробивая в них отверстия в соответствии с кодом, немного похожим на шпионский шифр. В то время как у шпионов бывают в ходу таинственные символы, для компьютеров применялся код из отверстий и их отсутствия. В отличие от шпионского кода, в компьютерном коде значения символов должны быть известны всем заинтересованным лицам. Специальный код, который до сих пор используют в компьютерах для простых чисел, называется двоичным.

На рис. 8 приведен пример перфокарты для числа 22. Чтобы увидеть, как использовать перфокарты для поиска данных с помощью магического принципа «шиворот-навыворот», давайте сделаем их сами, а потом посмотрим, как они действуют.

Шаблоны для перфокарт можно скачать здесь: www.cs4fn.org/punchcards/.

Распечатайте их — в идеале прямо на тонком картоне — и слегка посыпьте тальком, чтобы они не склеивались (это важно).

Вместо отверстий и их отсутствия мы будем использовать в нашем коде отверстия и небольшие вырезы. Вам следует сделать вырезы в нужных местах, чтобы в сумме получилось число, крупно написанное на карте. Например, на карте 22 есть вырезы напротив 16, 4 и 2, а 16 + 4 + 2 = 22. Чтобы понять происходящее, нужно знать кое-что из простой математики, а именно двоичную систему счисления.

Две системы

Двоичный код — это способ записывать числа, при котором в нашем распоряжении 0 и 1 вместо 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, которыми мы обычно пользуемся. Наша обычная система называется десятичной. В двоичной системе всего два символа, и на перфокартах мы будем использовать круглые отверстия для 0 и щели для 1. Двоичная и десятичная системы — просто две разные системы представления чисел. Выбрать правильное представление информации — еще один важный элемент вычислительного мышления.

Давайте сначала рассмотрим десятичную систему и сравним ее с двоичной. В десятичной системе, чтобы досчитать до 9, мы используем цифры, но они заканчиваются, и в этот момент мы переходим в новый столбик. Мы возвращаемся к 0, но переносим 1 в следующий столбик, и 1 теперь обозначает 10, как показано на рис. 9.

Любая цифра во втором столбике обозначает на 10 больше, чем та же цифра в первом столбике. В десятичной системе 16 — это один десяток (1 в столбике десятков) и шесть единиц (6 в столбике единиц). Мы добавляем 10 к 6, чтобы получить число 16. Подобным образом, 987 обозначает 9 раз по 100, 8 раз по 10 и 7 раз по одному, сложенные вместе.

Двоичная система работает точно так же, только у нас раньше заканчиваются цифры. Дойдя до 1, мы уже переходим в новый столбик, до 9 нам не добраться (рис. 10). Это значит, что столбцы теперь предназначены для единиц, двоек, четверок, восьмерок и так далее — вместо единиц, десятков и сотен. То есть в двоичной системе (используя только 1 и 0) мы записываем, например, число 5 как 101. Это 1 в разряде четверок плюс 0 в разряде двоек и плюс 1 в разряде единиц.

Если распределить это на пять колонок (как мы сделаем это на перфокартах), то 5 в двоичной системе будет выглядеть как 00101.

Подобным образом, 16 в двоичной системе — это 10000.

Отметим, что, помимо колонки единиц, все остальные колонки обозначают степени двойки, то есть четные числа. Поэтому единственный способ представить нечетное число в двоичной системе — поставить 1 в колонку единиц. У всех нечетных чисел в ней будет 1, а у четных — 0. Насколько это важно, мы увидим ниже.

Двоичные перфокарты

Какое отношения это имеет к нашим перфокартам? На них мы можем записывать числа в двоичной системе, используя отверстия для 0 и вырезы для 1. Чтобы записать на перфокарту число 5, начиная слева, нам нужно отверстие (0), еще отверстие (0), потом вырез (1), снова отверстие (0) и, наконец, вырез (1). Для числа 16 (10000) нам нужен один вырез и 4 отверстия. Если у нас есть место для пяти отверстий, мы можем записать на карту любое число до 31. Имея достаточно места (то есть достаточно степеней двойки и, соответственно, разрядов), мы можем записать любое число. Описанные примеры перфокарт приведены на рис. 11а и 11b.

Как только мы записали на карту число в двоичном коде в виде отверстий и вырезов, можно с легкостью найти любую карту. И здесь наступает черед метода «шиворот-навыворот».

Возьмите стопку карт и убедитесь, что они сложены срезанными уголками друг к другу, а отверстия выровнены в одну линию. Теперь вставьте карандаш в крайнее правое отверстие (колонку единиц) и стряхните все карты, у которых в этом месте вырез (как мы помним, это нечетные числа). У вас останутся только карты с 0. Теперь вернитесь к числу, которое вы хотите найти. Если в его двоичном коде в конце стоит 0, то сбросьте нижнюю стопку — те карты, которые вы стряхнули. Если в целевом числе там стоит 1, то оставьте нижнюю стопку. Повторите то же самое для каждого отверстия по очереди.

Например, мы ищем карту с номером 16. В двоичной системе это 10000. При движении слева направо выходит:

ВЫРЕЗ 1: 0 — СБРОСЬТЕ упавшие карты.

ВЫРЕЗ 2: 0 — СБРОСЬТЕ упавшие карты.

ВЫРЕЗ 4: 0 — СБРОСЬТЕ упавшие карты.

ВЫРЕЗ 8: 0 — СБРОСЬТЕ упавшие карты.

ВЫРЕЗ 16: 1 — ОСТАВЬТЕ упавшие карты.

Многократно сбрасывайте нижнюю стопку, пока, в пятом раунде, ее не нужно будет оставить. У вас останется карта с номером 16. Таким образом, прорабатывая двоичный код, можно найти любую карту. Попробуйте найти карту 5. В двоичной системе это 00101. При движении справа налево получаем:

ВЫРЕЗ 1: 1 — ОСТАВЬТЕ упавшие карты.

ВЫРЕЗ 2: 0 — СБРОСЬТЕ упавшие карты.

ВЫРЕЗ 4: 1 — ОСТАВЬТЕ упавшие карты.

ВЫРЕЗ 8: 0 — СБРОСЬТЕ упавшие карты.

ВЫРЕЗ 16: 0 — СБРОСЬТЕ упавшие карты.

У вас останется карта 5.

Как же это работает?

Оказывается, сбрасывая карты таким образом, вы поступаете как фокусник, сдающий карты по принципу «шиворот-навыворот». Чтобы это увидеть, нужно снова подключить логическое мышление и с его помощью найти точное объяснение происходящему.

Возьмите первый раунд, когда вы сбрасываете карты и одновременно ищете номер 16. Стряхнув первые перфокарты и затем избавившись от них, вы отметаете все карты с вырезом (1) в первой позиции двоичного числа. Это столбик единиц. У чисел 1, 3, 5, 7 будет вырез (1) в этой позиции — все это нечетные числа. Происходит то же самое, что и в первом раунде «шиворот-навыворот», когда мы сбрасываем каждую вторую карту. Как вы видели выше, мы переводим число из двоичной системы в десятичную, складывая числа в соответствующих разрядах (например, 5 = 4 + 0 + 1). Этот последний разряд единиц полностью определяет нечетные числа, в то время как все остальные — четные (2, 4, 8, 16, …).

Вот еще один способ понять, почему двоичное представление ведет к тому, что нечетные числа отбрасываются, — он поможет нам понять, как работает остальная часть фокуса. Подумайте, как мы считаем в двоичной системе: 0, 1, 2, 3, 4, … — это 000, 001, 010, 011, 100, … В колонке единиц во время счета значение меняется через раз, то есть в этой последней позиции по очереди оказываются 0, 1, 0, 1 — и так далее. Это значит, что если мы отбросим все единицы, то избавимся от каждой второй карты.

То есть мы показали, что в первом раунде происходит то же самое, что и в фокусе. Отбросив все карты с нечетными цифрами, мы переходим к следующему отверстию на перфокарте и, таким образом, к следующей позиции в двоичном числе. Эта операция убирает все числа, в составе которых есть разряд двоек. Например, это 6 (110 в двоичной системе), поскольку 6 = 4 + 2 + 0. На этот раз уходят 2 (10 в двоичной системе), 3 (11), 6 (110), 7 (111), 10 (1010), 11 (1011) и так далее. Однако нечетные числа уже были удалены, значит, на этот раз мы стряхнем 2, 6, 10, ... То есть остается каждая вторая карта. Это та же последовательность карт, которую мы удаляем во втором раунде «шиворот-навыворот».

Причина становится очевидной, если посмотреть на второй столбик в числах, записанных двоичным кодом. Там мы видим 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1 ...

Получается, что в двоичной записи второй символ меняется только в том случае, если в первой позиции уже были и 0, и 1. Но если убрать каждую вторую карту в этой последовательности, у нас остается не 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1 ..., а 0, 1, 0, 1, 0, 1, ... И мы получаем:

Взяв перфокарты, оставшиеся на этом этапе, мы, по сути, повторяем то же самое, что и в первом раунде, — сбрасывая все карты с 1, мы убираем каждую вторую карту, поскольку 1 стоит в середине каждого второго числа в приведенной последовательности.

То же происходит с оставшимися картами в последующих раундах. Мы всегда стряхиваем каждую вторую карту из оставшихся. Разница здесь в том, что числа на перфокартах отражают не позицию карты, но ее маркировку отверстиями и вырезами. То есть их можно перемешать, и мы все равно найдем нужную перфокарту. Еще одно различие состоит в том, что перфокарты убираются в один прием — параллельно. Метод «шиворот-навыворот» был очень медленным и скучным, потому что приходилось разбираться с каждой картой по очереди. Версия с перфокартами очень быстрая.

С точки зрения информатики в нашем фокусе используется последовательный алгоритм: мы выполняем одну операцию за один прием, перемещая карту за картой. Большинство компьютерных программ написаны именно так — инструкции выполняются одна за другой. Поиск перфокарт — пример параллельного алгоритма. Вместо того чтобы делать одну вещь за раз, мы, по крайней мере на некоторых этапах, делаем много вещей одновременно, сбрасывая много карт. Игральные карты сдаются довольно медленно, а перфокарты отсеиваются быстро. Параллельные алгоритмы — будущее программирования. С каждым новым поколением информационных технологий нам доступно все больше процессоров как в компьютерах, так и в других электронных приборах, окружающих нас, потому что технологические возможности растут. Это относится и к так называемым многоядерным процессорам — когда на одном чипе работает несколько компьютеров. Кроме того, мы можем создавать еще более масштабные компьютерные сети, которые способны эффективно работать над решением одной проблемы. Поэтому, чтобы добиться большей производительности, нужно писать алгоритмы так, чтобы все доступные процессоры всегда были заняты чем-то полезным, то есть нам необходимы параллельные алгоритмы.

Еще одна причина, по которой алгоритм с перфокартами работает быстро, — применение подхода «разделяй и властвуй» к поиску. Этот случай похож на рассматриваемый нами в предыдущей главе. Более того, мы продолжаем говорить об алгоритмах поиска — с некоторым обобщением. Мы ищем игральную карту и перфокарту. «Разделять и властвовать» — широкий способ решать задачи очень быстро, и он бывает полезен не только в ситуациях, связанных с поиском. Как мы видели, секрет здесь в том, чтобы многократно сокращать задачу вполовину. Что это значит в случае с нашими картами? В каждом раунде мы убираем половину имеющихся карт. Как мы проводим поиск среди оставшихся? Делаем то же самое — убираем половину, и еще половину, и еще половину. Однако здесь деление пополам происходит в двоичной записи чисел, а не физически.

Осознав, что перед нами проблема поиска, мы понимаем, что есть и другие способы поиска перфокарты — например, решения, действенность которых мы видели в предыдущей главе. Самое простое — проверять каждую карту по очереди. Это линейный поиск. Наш алгоритм «разделяй и властвуй» дает результат гораздо быстрее потому, что на каждом этапе задача сокращается наполовину. Если бы карты были расположены по порядку, мы могли бы использовать двоичный поиск для обнаружения нужной карты. Это быстрый способ, однако наш новый способ в этой ситуации еще быстрее — он действует даже в том случае, если перфокарты перетасованы.

И снова изобретаем фокусы

Новое из старого

Фокусы придумывают примерно так же, как программисты пишут программы. Обычно они не начинают с нуля, а приспосабливают для своих нужд части существующих программ, которые выполняют схожие задачи. Поэтому, если мы хотим придумать новый фокус, лучше взять уже работающий трюк и превратить его во что-нибудь новое. Один и тот же ключевой алгоритм можно приспособить для разных целей. Здесь мы опять наблюдаем обобщение в действии. Фокусник берет ключевую идею существующего фокуса и обобщает ее.

Другой пример — переделать старый трюк, объединив известные нам шаги из разных фокусов. Здесь мы используем декомпозицию. Объединив несколько старых приемов, мы получаем нечто новое. Например, если вы владеете приемом ложной тасовки — делаете вид, что тасуете всю колоду, но оставляете средние карты в прежней последовательности в конце колоды, — то эффект будет еще более магическим.

Третий способ — изменить презентацию фокуса. Если вы придумали основной механизм, на котором строится хороший фокус, используйте его еще раз, но уже совершенно по-новому. Например, для того же алгоритма можно использовать другую историю или внести более существенные изменения, как мы увидим ниже.

Новые фокусы с помощью информатики

Как мы уже знаем, алгоритмические фокусы и компьютерные программы — по сути, одно и то же. В некоторых фокусах применяются точно такие же алгоритмы, как и в программах, — например, поисковый. Значит, мы вправе применить обобщение и повторно использовать некоторые решения. В описанном фокусе надо было найти 16-ю карту, но на примере перфокарт мы видим, что, если перевести числа в двоичный код и таким образом определить, какую стопку оставить, можно выделить любую карту. А значит, эту идею легко вернуть в мир магии. Например, подготовить фокус, в котором перед показом карту можно положить куда угодно. И это необязательно должна быть 16-я карта! Конечно же, при этом необходимо точно знать, где она находится. Еще надо уметь переводить числа в двоичный код в уме. Проводить математические операции в уме — полезный навык и для фокусника, и для ученого-информатика!

Однако пойдем немного дальше и не просто слегка изменим фокус, как мы сделали ранее. Если абстрагироваться от происходящего и выделить математический принцип, стоящий за алгоритмом, то есть скорее результат, а не шаги, приводящие к нему, то вы придумаете совершенно новый фокус.

Выберите стопку

Давайте посмотрим, как этот принцип работает в «Сне об австралийском маге». Как мы увидели на примере перфокарт, он работает, потому что на каждом этапе мы сбрасываем и оставляем некий набор чисел в зависимости от их представления в двоичной системе. На первом этапе уходят перфокарты с нечетными числами, то есть с 1 в первой позиции двоичного кода (в первом колонке) — это 1, 3, 5, 7, … (0001, 0011, 0101, 0111, …). В следующем раунде мы отбрасываем числа 2, 6, … Это карты с 1 во второй позиции двоичного кода (во втором колонке), то есть 0010, 0110, … Это не все карты, у которых есть 1 в этой позиции, потому что некоторые мы уже отбросили. Давайте перечислим все такие карты. У нас получится более длинный список: 2, 3, 6, 7, 10, … (0010, 0011, 0110, 1111, 1010, …). В следующий раз избавляемся от карт с 1 в третьей позиции двоичного кода (колонке четверок). В полный список войдут 4, 5, 6, 7, 12, … (0100, 0101, 0110, 0111, 1100, ...). Теперь стоит отметить, что мы наблюдаем здесь еще одну модель. Первое число в каждом списке карт указывает на колонку в двоичном коде, которой соответствует весь список.

На этом основан еще один фокус. Сделайте стопку карт, на которых написаны числа 1, 3, 5, 7, 9, 11, 13, 15. Сделайте еще одну стопку карт, с числами 2, 3, 6, 7, 10, 11, 14, 15. Сделайте третью стопку, с 4, 5, 6, 7, 12, 13, 14, 15. И наконец, четвертую, с 8, 9, 10, 11, 12, 13, 14, 15. Перетасуйте карты в каждой стопке. Сами стопки могут идти в любом порядке.

Теперь попросите добровольца задумать число от 1 до 15 и запомнить его, но не говорить вам. Возьмите одну из стопок и сдавайте карты по одной. Объясните, что вы читаете мысли человека, который смотрит на карты, даже не глядя на него. Вам достаточно смотреть на карты. Когда вы закончите сдавать карты, попросите добровольца сказать, было ли задуманное число в этой стопке, что является «дополнительной проверкой на детекторе лжи», которая поможет вам настроиться на его мысли. Если доброволец скажет, что число было в стопке, отложите карты в сторону. Если нет, оставьте их на месте. Повторите эту процедуру с каждой стопкой.

После четвертой стопки назовите число, которое задумал доброволец! Как же вы это сделали?

Достаточно запомнить самое маленькое число в каждой отложенной стопке. Сложите их, и получится число, которое задумал человек. Почему? Эти самые маленькие числа отражают разряд в двоичном коде, который есть во всех картах из этой стопки. Так, если стопка отброшена, то загадочное число имеет 1 в этом разряде. Сложите эти малые значения, и вы переведете число из двоичного кода в десятичный. Например, если сброшены стопки 1 и 4, это значит, что искомое число — 0101 в двоичном коде или 5 в десятичном (0 × 8 + 1 × 4 + 0 × 2 + 1 × 1 = 4 + 1 = 5).

Таким образом, у вас появился новый фокус на основе той же математической модели, что и предыдущий.

Примечание фокусника

Считается, что принцип 16-й карты стал известен в 1958 г., когда программист и известный фокусник Алекс Элмсли опубликовал фокус «7–16» в журнале фокусников Ibidem. Он известен в среде фокусников благодаря манипуляции с картами, названной в его честь «счет Элмсли».

От фокусов к программам и наоборот

Итак, понимание информатики и математических принципов, стоящих за ней, поможет вам придумывать новые фокусы. Более того, справедливо и противоположное. Фокусники много раз изобретали нечто новое в информатике благодаря своим трюкам. Люди, придумывающие фокусы, делают то же самое, что и люди, придумывающие алгоритмы для компьютеров, — пишут новые программы. Возможно, вы слышали, что опытных программистов называют волшебниками. Программисты и в самом деле волшебники!

Глава 4
Головоломки, логика и образцы

Как решать головоломки? Несомненно, логическое мышление — главное, что для этого необходимо, но важнейший секрет мастеров именно обобщение и сопоставление с образцом. Эти приемы используют, чтобы разгадывать головоломки, писать программы и заниматься многими другими вещами — от игры в шахматы до тушения пожаров. Логическое мышление, обобщение и сопоставление с образцом также играют главную роль в вычислительном мышлении.

Головоломки «Улей»

Логические головоломки

Если вам нравятся головоломки и вы хорошо их решаете, то, вероятно, вам понравится информатика. В этой сфере умение мыслить логически необходимо прежде всего. Это относится к информатике в целом, но особенно важно при написании программ. Программы основаны на логике, и, как мы уже видели, важно четко увидеть все варианты, чтобы написать хороший код (и придумать хороший фокус). Программы должны работать при любых обстоятельствах, поэтому, и создавая, и оценивая их, программисту необходимо тщательно прорабатывать мелочи.

Говоря о логическом мышлении, в определенном отношении мы подразумеваем способность мыслить ясно и учитывать даже небольшие детали. Однако есть и более глубокий смысл — умение работать с математической логикой, и если вы им обладаете, то будете успешно выдвигать неопровержимые аргументы. Логически обоснованные аргументы неоспоримы, и еще древнегреческие философы осознали их важность. Умение найти неоспоримые аргументы полезно людям любых профессий, а не только программистам. Это нужно и для решения головоломок, только здесь оно сведено к чистой логике. Как и любой другой навык, логическое мышление можно освоить и улучшить. Для этого необходима практика (надо много тренироваться, как и в любом другом случае), разгадывание головоломок — приятный способ ее получить. Чем больше вы решаете головоломок, тем больше полезных хитростей подскажет вам вычислительное мышление.

Соты в улье

Существует великое множество разного рода головоломок, и все они рассчитаны на умение мыслить логически. Вы наверняка видели судоку в специальных сборниках или в газетах. Это головоломки, которые представляют собой сетку с числами. Давайте рассмотрим логическое мышление на примере более простой головоломки, которая называется «Улей». Идею для нее мы почерпнули у японского автора головоломок Наоки Инаба.

Головоломка «Улей» представляет собой блок из шестиугольников — символический улей с сотами. Его участки разделены толстыми линиями. Заполняя улей, необходимо соблюдать два правила.

1. В каждой выделенной области должны находиться числа от 1 и до числа, равного количеству шестиугольников в области. Например, самый верхний уровень в головоломке на рис. 12 состоит из четырех шестиугольников, поэтому их надо заполнить числами 1, 2, 3 и 4. Числа нельзя повторять. Если в области всего два шестиугольника, как на этом рисунке, то нужно внести числа 1 и 2.

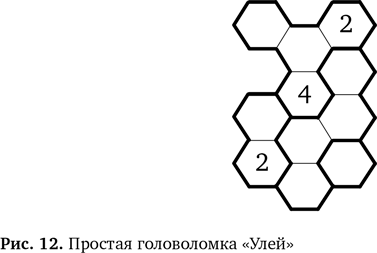
2. Шестиугольники с одинаковыми номерами не могут соприкасаться ни с одной гранью. Таким образом, поскольку в улье на рис. 12 в среднем шестиугольнике стоит 4, ни в одном из пяти, окружающих его шестиугольников 4 стоять не может.

На рис. 12 представлена простая головоломка «Улей», которую мы предлагаем решить. Попробуйте сделать это, прежде чем продолжить чтение.

Решаем головоломку «Улей»

Вот логические рассуждения, с помощью которых мне удалось решить головоломку. Мои рассуждения основаны на правилах, форме улья и уже данных числах. В этих рассуждениях показано, почему заполненная головоломка, которую я считаю решением, действительно является решением.

В правой нижней части улья есть участок, состоящий лишь из одной ячейки. В соответствии с первым правилом, в ней должно стоять число от 1 до… 1. Поэтому я ставлю туда 1, как на рис. 13.

Наконец, слева внизу у нас есть область из двух ячеек. В них должны стоять 1 и 2 (по первому правилу). В одном шестиугольнике уже есть 2, так что единственный вариант для оставшегося шестиугольника — это 1 (рис. 14).

В двух оставшихся областях — по четыре шестиугольника. Сейчас нам придется поломать голову. Посмотрите на 1 в нижнем углу. Это значит, что ни в одном из трех окружающих его шестиугольников не может быть 1 (по второму правилу). Однако в этой области есть только четыре шестиугольника, и один из них должен содержать 1 (по первому правилу). Значит, 1 должна находиться в последнем шестиугольнике, который не соприкасается с 1, потому что в другое место единицу не поставишь. Мы получаем улей с рис. 15.

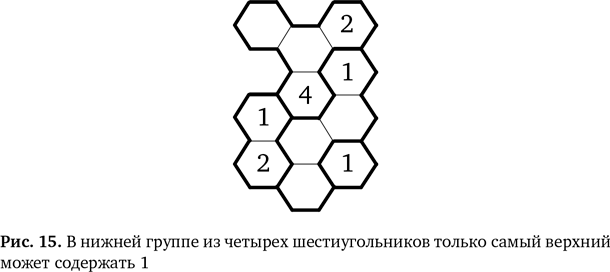
Теперь постараемся понять, куда в этой же области нужно поставить 2. Оба нижних шестиугольника соприкасаются с 2, и единственно, куда можно написать 2, — в ячейку между двумя единицами справа внизу (рис. 16).

Над этой областью стоит 4, и рядом нельзя поставить еще 4 — ее нужно расположить внизу. Это определяет, где должны оказаться 3 и 4 относительно остальных шестиугольников, как показано на рис. 17.

Итак, у нас осталась верхняя область. Заполняем ее, рассуждая похожим образом. В прилегающей области стоит 1, значит, единственное возможное место для последней 1 — верхний левый угол, как на рис. 18.

Соответственно, в последний шестиугольник надо поставить 3, поскольку в этой области должны стоять числа 1–4 и недостает только 3. Решение целиком показано на рис. 19.

Мы разгадали головоломку. И сделали это, исходя из двух правил и исходных данных — известных чисел. Основываясь на них, мы многократно выявляли новые факты в этой головоломке. Мы прибегли к особому виду логических рассуждений, называемому дедукцией, который позволяет с помощью известных фактов и правил мироустройства (в данном случае — правил головоломки) получать новые факты. Считается, что именно так Шерлок Холмс творил свои детективные чудеса. Он подмечал разные детали в людях и ситуациях, а потом с помощью дедукции выводил новые факты, которые являлись следствием этих деталей. Чем больше фактов он узнавал, тем дальше мог продвинуться в дедукции, что и позволяло в конечном итоге раскрывать преступления. Ученые-информатики и математики используют похожий метод. Хорошие программисты обращаются именно к дедукции, чтобы убедиться в бесперебойной работе своих программ.

Выводим правила

Сопоставляем с образцом и создаем правила

До сих пор мы выводили факты непосредственно из двух правил. Но решив много головоломок и обретя опыт, мы берем на вооружение другой подход — используем естественные навыки вычислительного мышления, например сопоставление с образцом из ранее встречавшихся ситуаций. Этот метод позволяет решать головоломки быстрее и тратить меньше времени на их обдумывание. Следующий шаг — обобщение, то есть для поиска образцов мы расширяем круг ситуаций, а не возвращаемся к уже известным. При наличии опыта мы начинаем создавать новые, ускоренные и универсальные правила, которые позволяют вести логические рассуждения на более высоком уровне. Это становится возможным благодаря использованию логического мышления не с целью решить конкретную головоломку, как мы делали до сих пор, но с целью создать новые правила. При этом мы уверены, что эти новые правила гарантированно выведены из основных. Давайте посмотрим, о чем идет речь, на некоторых примерах.

Правило одного шестиугольника

Вернемся к решению предыдущей головоломки. Мы выяснили, что, если в области содержится только один шестиугольник, в нем должна стоять 1. Это следует непосредственно из первого правила. Осознав, что нет необходимости снова это обдумывать, мы можем из начального правила вывести новое.

3. ЕСЛИ в области есть только один шестиугольник, ТО в нем может стоять только 1.

Чтобы наглядно представить это правило и не ограничиваться словами, мы набросаем схему (рис. 20). Стрелка показывает, какие изменения мы вносим в улей. Слева изображена позиция сопоставления с образцом, а справа — вносимые изменения, если найдем образец. Подобные правила называются порождающими правилами, правилами логического вывода или правилами подстановки. Наше правило в виде схемы показывает, что если мы найдем пустой участок в один шестиугольник, то можем преобразовать его в шестиугольник с 1.

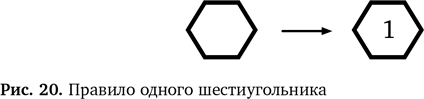
Теперь можно применять это правило, даже не задумываясь, почему оно работает. Наше логическое мышление теперь оперирует на более высоком уровне, по крайней мере в такой простой ситуации.

Правило двух шестиугольников

Теперь выведем еще одно новое правило для областей, состоящих из двух шестиугольников. Мы видели, что если есть область из двух шестиугольников и в одном стоит 2, то во второй нужно поставить 1 (рис. 21).

Мы вправе рассматривать это как обобщенное правило из конкретного примера нашей головоломки. Не важно, в каком шестиугольнике стоит 2, — логика не меняется. Даже если картинку перевернуть, правило останется прежним. Это правило применимо и к шестиугольникам, соприкасающимся по диагонали в любом направлении. Но обобщение можно продолжить. По той же логике, если в области из двух шестиугольников в одном уже стоит 1, в другой нужно поставить 2. Это показано на рис. 22.

Объединив два эти отдельные правила, мы получаем полное обобщенное правило:

4. ЕСЛИ один шестиугольник в области из двух содержит 1 или 2,

ТО в другом шестиугольнике будет второе число из этих двух.

Правило можно представить в виде схемы, где x будет обозначать любое число (точно так же, как математики используют x и y для обозначения переменных в алгебре).

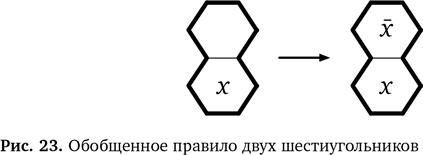
В одном случае x заменяет 1, а в другом — 2, но замена остается неизменной в рамках одного примера. Схема правила приведена на рис. 23. На схеме x обозначает другое число. То есть если x — это 1, то x — это 2 и если x — это 2, то x — 1. Это правило подходит для области из двух шестиугольников, повернутой в любую сторону, и не важно, какое число стоит наверху, а какое — внизу. Схема превращается в одно из изначальных правил (и их схем), если заменить x на 1 или 2. Так мы начали изобретать своего рода математические обозначения, которые используются с той же целью, что и символы в математике. Они дают возможность говорить о вещах с большой точностью, и это важно, так как по мере усложнения правил надо стараться избегать возможных ошибок.

Вместо того чтобы выводить новые факты из заданных фактов, используя исходные правила решения головоломки, мы теперь выводим новые, «более крупные» правила с учетом исходных. Это называется производные правила логического вывода. Когда мы видим ситуацию, соответствующую образцу из какого-то нового правила, мы уже не думаем, почему оно верно, а просто применяем его. Мы абстрагировались от обоснования, стоящего за правилом.

Правило угла

Давайте рассмотрим последний пример создания более общего правила на базе нашего для решения простой головоломки. Оказывается, он весьма полезен. Мы поняли, куда поставить 1 в области из четырех шестиугольников в нижнем углу. Это было возможно, потому что в прилегающей области уже стояла 1, устроившаяся в углу, как показано на рис. 24.

Единицу нужно поставить в позицию a, b, c или d (рис. 24). Однако в соответствии со вторым правилом головоломки рядом не должна находится ячейка с 1. Значит, позиции b и с исключаются. Остается только позиция d, и только туда получается поставить 1. Мы можем изобразить этот этап в виде схемы для правила замены (рис. 25).

Конечно, в любых пустых шестиугольниках уже могут стоять числа, но правило остается справедливым — это еще один способ обобщить наше новое правило. Кроме того, число, которое мы используем при сопоставлении с образцом, необязательно должно быть 1. Это может быть любое другое число в рамках достаточно большой области. Если мы опять поставим x на место любого возможного числа, то наше правило становится обобщенным вариантом (рис. 26).

Мы даже можем продолжить обобщение нашего правила. Область, которую мы заполняем, не должна иметь заданную форму. Следующий шестиугольник может стоять в любой позиции у дальнего края более крупной области — везде, где он связан с угловым шестиугольником, но не касается его. В варианте правила угла на рис. 27 мы использовали вопросительные знаки, которые показывают возможные положения этого шестиугольника.

Получаем обобщенное правило:

5. ЕСЛИ шестиугольник соседствует с областью из четырех шестиугольников и только три из четырех соприкасаются с ним, ТО в четвертом будет стоять то же число, что и в указанном вначале шестиугольнике.

Как и в предыдущих случаях, правило применимо при любом положении схемы — перевернутом, горизонтальном, под углом или отраженном. Возможно, вы найдете больше способов обобщить правило.

Итак, сейчас у вас есть вышеприведенное общее правило. Если в головоломке вы увидите ситуацию, сопоставимую с образцом, правило можно применить. Вставьте пропущенное число, которое соответствует x.

Записываем правила

Большинство при решении головоломок не записывают правила, которые они выводят и используют. Люди просто запоминают сработавший метод и, особенно не задумываясь, по возможности применяют его. Однако специалисты по информатике любят записывать такое. Зачем это делать? Примерно по тем же причинам, что и записывать алгоритмы. Их можно использовать, например, чтобы научить других разгадывать головоломки (как это сделали мы), и тогда им не придется проходить весь этот путь с самого начала. Правила можно использовать, чтобы научить компьютер разгадывать головоломки. Кроме того, это делается ради точности. Довольно часто возникают ложные воспоминания о сработавших правилах, или мы можем выучить их, не до конца уловив детали. В любом случае в результате правило может использоваться неверно или в новой ситуации, которой оно не очень соответствует. Если записать все точно, то мы избежим такого рода ошибок.

Но здесь уже не получится использовать рисунки, как сейчас. В информатике для записи правил используют математические обозначения (формальную логику). Языки для описания этой логики немного похожи на языки программирования, но при этом они очень гибкие. Их большое преимущество состоит в том, что их легко обработать на компьютере, и затем на их основе компьютер может строить логические рассуждения. Так логика становится основой для компьютерных программ, которые позволяют решать головоломки.

Многие системы искусственного интеллекта основаны на идее использования порождающего правила. Вместо того чтобы рисовать схемы, мы пишем правила в следующем виде:

ЕСЛИ <какая-то ситуация> ТО <действие, которое надо выполнить>

Список таких правил представляет собой программу. Если правило работает, то компьютер может выполнить действие. Если совпадают несколько правил, он выбирает любое, и все повторяется снова и снова. Такой подход обеспечивает новую парадигму для создания программ и позволяет совершенно по-другому увидеть их сущность. Это не просто последовательность команд для выполнения, о которой мы говорили до сего момента, а новый тип мышления.

Все лучше осваивая искусство решения головоломок, мы не просто используем логическое мышление, а сопоставляем с образцом текущую ситуацию, чтобы узнать, какое правило нужно применить. Программа, основанная на порождающих правилах, делает похожее сопоставление с образцом. Это простое вычислительное мышление.

Когда мы записываем правила для создания программы, обобщение идет рука об руку с абстрагированием. Мы скрываем подробности, касающиеся других частей головоломки, чтобы было легче продумывать, как шире обобщить правила. На схеме, иллюстрирующей наше последнее правило, мы использовали несколько абстракций, чтобы описать, как осуществлять сопоставление с образцом. Например, переменная x — это абстракция. Мы абстрагируемся от конкретного числа (то есть опускаем подробности) — правило применимо независимо от числа. Кроме того, мы используем знак вопроса в качестве другой переменной, чтобы абстрагироваться от конкретного положения четвертого шестиугольника в нашем представлении правила. Подобным образом мы абстрагируемся от ориентации схемы — ее можно как угодно вращать или отражать, но она будет соответствовать решаемой головоломке.

Другие головоломки

Еще один простой «Улей»

На рис. 28 представлена новая головоломка. Посмотрите, можно ли использовать приведенные выше правила для ее решения. В процессе разгадывания вы найдете новые правила. Если ни одно из выведенных ранее правил не подойдет, возможно, стоит вернуться к исходным. Помните, что по второму правилу два одинаковых числа не могут находиться рядом. Ответ приведен в конце главы.

Головоломка посложнее

На рис. 29 показана еще одна головоломка, значительно больше и сложнее. Решая ее, выводите новые правила — те, что пригодятся при решении этой головоломки, и те, что могут пригодиться в будущем.

СОВЕТ. Когда будете искать новое правило, обратите внимание на то, что происходит, когда области из трех шестиугольников граничат друг с другом.

Логическое мышление и опыт

Важность логики

Какую роль логическое мышление играет в информатике? Центральную. Работа компьютеров основана на логике, а значит, чтобы программировать их, давать им указания, нужно мыслить логически. В противном случае вы с большой вероятностью ошибетесь.

Логическое мышление — один из ключевых компонентов вычислительного мышления, которое проходит через все его аспекты, и не важно, какая стоит задача — создавать алгоритмы или оценивать их. Программистам необходимо мыслить логически, когда они разрабатывают новую программу, переделывают уже существующую под новые задачи, ищут дефекты программного кода или проводят иную оценку.

В информатике используются очень простые и точные языки математической логики. Как и наши головоломки, эти языки имеют набор правил, называемых аксиомами. Наши два исходных правила головоломки являются для нее аксиомами. Так же, как и мы, математики выводят из аксиом правила более высокого уровня, что позволяет продвигаться в рассуждениях большими шагами.

Такие логические элементы формируют основу языков программирования и определяют, что означает каждая их конструкция. Поэтому люди, создающие программы, тоже должны рассуждать логически. Поскольку в основе языков программирования лежит логика, мы можем использовать логическое мышление, чтобы рассуждать о возможностях наших программ. Таким образом даже можно убедиться в правильности их работы. Для этого действия программы описывают на языке логики. Затем с помощью логических рассуждений подтверждают, что программа дает именно задуманный эффект.

Мы также увидели, что программисты изобрели способы приравнять логические правила к собственно программам — это называется логическое программирование. Чтобы написать такую программу, надо разработать правила, на основании которых можно произвести определенные вычисления. Правила для нашей головоломки, записанные на языке логического программирования, могли бы стать программой для решения задач. И какой бы язык программирования вы ни использовали, логическое мышление придется применять обязательно.

Специалисты за работой

Чем больше у нас опыта в разгадывании головоломок, тем больше правил накапливается в уме и тем быстрее и легче мы решаем новые задачи. Именно так гроссмейстеры играют в шахматы. Они видят в текущих позициях ситуации, похожие на те, что им уже встречались, и делают ход, подсказанный опытом. Это позволяет не перебирать огромное количество ходов наперед, что у человека происходит медленно и порой с ошибками. Компьютеры играют именно так — перебирают массу вариантов и смотрят, какие будут последствия. Люди-шахматисты играют гениально, потому что используют как логическое мышление, так и сопоставление с образцом; кроме того, у них накопилась масса неформальных правил.

Так поступают не только профессиональные шахматисты. Есть предположение, что это свойственно практически всем специалистам независимо от навыка, которым они прекрасно овладели. Например, когда пожарные успевают выбраться из горящего здания прямо перед обвалом крыши, это происходит благодаря сопоставлению с образцом, только процесс идет подсознательно. Интуиция — подсознательное сопоставление с образцом на основе богатого прошлого опыта.

Если вы хотите стать специалистом в любой области, развивайте навыки сопоставления с образцом и обобщения. Есть универсальный принцип, который позволяет овладеть любым навыком до уровня гения и стать невероятно успешным, — нужно потратить 10 000 часов на тренировки. Столько времени тратят на занятия скрипачи-виртуозы. Подобным образом самые успешные программисты (те, кто стал миллиардерами) примерно столько учились писать программы. Даже тибетские монахи, известные безмятежностью и способностью сострадать, практиковали медитацию примерно столько же времени, чтобы достичь внутреннего покоя.

Если вы хотите в совершенстве овладеть программированием, начинайте практиковать вычислительное мышление прямо сейчас. И даже если вы не собираетесь стать программистом, развивая такие навыки, как логическое мышление, обобщение, абстрагирование и сопоставление с образцом, вы добьетесь больших успехов в любой профессии. Логические головоломки — занимательный способ тренировать эти навыки, особенно если будете обдумывать процесс и записывать правила.

Ответы

На рис. 30 и 31 показаны решения для двух последних головоломок «Улей».

Глава 5
Головоломные маршруты

Найдите для шахматного коня способ побывать в каждой клетке на доске ровно один раз, решите проблему экскурсовода и, наконец, проведите консультацию в информационном центре для туристов. Сделайте все это как можно лучше, используя вычислительное мышление. Да, и еще помогите туристам упаковать чемоданы. Алгоритмы находятся в центре вычислительного мышления и позволяют нам решить задачу один раз — и больше не думать о ней никогда. Однако выбрать хороший способ для представления используемой информации — еще один важный аспект вычислительного мышления. Сделайте это хорошо, и составить алгоритм будет гораздо легче.

Две задачи

Задача «Ход конем»

В головоломке «Ход конем» один шахматный конь может передвигаться по небольшой доске в форме креста. Конь ходит на два поля в любом направлении, а потом на одно поле перпендикулярно этому направлению или наоборот. Он переходит на новое поле, не останавливаясь на полях между начальным и конечным, и всегда должен оставаться в пределах доски. Возможные первые ходы в головоломке показаны на рис. 32.

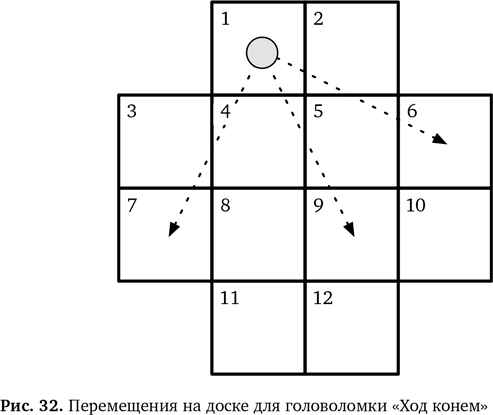
Вам нужно найти последовательность ходов, начиная с поля 1, чтобы конь побывал на всех полях ровно один раз и вернулся в исходную точку.

Решите это!

Попробуйте решить задачу «Ход конем», замерив, сколько времени у вас уйдет. При этом недостаточно, чтобы конь прошел заданный путь. Необходимо найти алгоритмическое решение, а не просто двигать фигуру по доске. Для этого нужно записать серию перемещений, которые приведут к ответу. То есть придется применить алгоритмическое мышление и вывести алгоритм для решения головоломки. Этот алгоритм можно записать в виде списка номеров, присвоенных полям, на которые ходит конь, в порядке прохождения. Или же записать алгоритм как серию команд вроде «перейти с поля 1 на поле 9». Решать вам.

Как только у вас появится работающий алгоритм, оцените его: проверьте, действительно ли работает это решение, опробовав его на практике. Следуйте собственным инструкциям, отмечая клетки по мере того, как их обходит конь. Таким образом вы сможете гарантировать, что он не нарушает правила и посещает каждую клетку ровно один раз. Если головоломка решена, прекрасно! Если нет, не беспокойтесь — ниже мы посмотрим, как облегчить эту задачу. Но сначала давайте попробуем решить задачу полегче.

Задача экскурсовода

Вы экскурсовод и работаете в отеле. Туристы из вашего отеля хотят отправиться на дневную экскурсию и посетить все достопримечательности города. Вам дали карту (рис. 33), на которой показано расположение достопримечательностей и указано, как добраться до них на метро.

Вам нужно составить маршрут, который начнется в отеле и позволит показать вашей группе все интересные места. Туристы прибыли в город всего на день и не хотят терять времени. Очевидно, они будут недовольны, если придется два раза проходить через одно и то же место. Также очевидно, что вечером они хотят оказаться в отеле.

Как и в случае с «Ходом конем», задача — найти алгоритмическое решение. Убедитесь, что ваше решение действительно работает. Сколько времени у вас ушло? Оказалась ли эта задача легче, чем предыдущая (то есть вы решили ее быстрее)?

Что необходимо?

Почему важно проверить, верно ли ваше решение? Ну конечно, вам не хотелось бы отправиться на экскурсию и в конце дня обнаружить, что вы пропустили важную достопримечательность. Кому хочется разбираться с недовольными туристами!

Чтобы проверить алгоритм, нужно провести процедуру, которую в информатике называют трассировкой. Это всего лишь означает, что сначала вы проходите все этапы алгоритма на бумаге. Вероятно, вы так и сделали, проверяя решения для «Хода конем». Для задачи, решаемой экскурсоводом, можно нарисовать маршрут на карте и, следуя инструкциям, помечать каждое посещенное место.

Конечно же, настоящий экскурсовод не удовлетворяется проверкой маршрута на бумаге. Он пойдет и проверит все в реальных условиях. Вы бы тоже пошли и проверили все сами, но, если сначала выполнить проверку на бумаге, это сэкономит массу времени. Программисты поступают точно так же. Сначала они проверяют, как программа работает на бумаге (трассировка), а потом испытывают ее в реальных условиях — проводят тестирование. Так же, как в случае с вашей задачей, программисты делают это, чтобы гарантировать бесперебойную работу программ.

Вообще, процедуру оценки можно сделать точнее. Для этого надо определить, какие именно особенности выполнения задачи важны, чтобы получить правильное решение. Если мы запишем список этих необходимых вещей, то сможем проверить, соответствует ли им найденное решение. В информатике такие особенности называются требованиями.

Для задачи экскурсовода нужно проверить, удовлетворяет ли итог следующим требованиям.

1. Экскурсия начинается в отеле.

2. Туристы посещают все достопримечательности.

3. Они не проходят одно и то же место дважды.

4. Экскурсия завершается в отеле.

Вернитесь назад и запишите список требований к головоломке «Ход конем». Видите что-нибудь похожее? Мы вернемся к этому ниже.

Почему это легко?

Возможно, вам показалось, что задача «Ход конем» сложнее, но на деле это не обязательно так. Решить ее будет очень легко, если использовать еще некоторые приемы из компьютерного мышления.

Почему задача экскурсовода легкая? Карта метро дает важную информацию, незначительные детали опущены. Это хороший пример абстракции — решение легко увидеть. Без карты было бы сложнее, даже если бы мы знали, где что находится. Карта метро — особый способ предоставления информации. Это особый вид схемы под названием граф. В информатике под графом подразумевают несколько кружков (мы называем их вершинами графа) и линий, которые их объединяют (ребра графа). Вершины и ребра представляют те аспекты данных, которые нас интересуют. Ребра показывают, какие вершины объединены таким образом, что это важно для решения нашей задачи. Туристические достопримечательности, вероятно, соединены автомобильными дорогами, но по-другому. В этом случае граф пути был бы другим — и он понадобился бы нам, если бы мы организовывали автобусный тур!

Это не важно!

Нас интересует, какие у нас есть достопримечательности (наши вершины) и какие из них соединены друг с другом линиями метро (наши ребра). Другие особенности этих мест нас не интересуют, поэтому мы их игнорируем. Мы опускаем их точное расположение, расстояние друг от друга, соединения автодорог и многие другие вещи, которые не относятся к нашей задаче — понять, как объехать все это на метро. Граф — это абстракция реального города. Мы спрятали все лишние детали, не нужные для построения графа. Здесь отражена только важная информация. Поэтому нам легко увидеть действительно необходимое для решения. Это хорошее представление текущей задачи.

Упрощаем

Графы часто используются, чтобы представить информацию о связях между объектами. Это маршруты на автобусных остановках, карты поездов и метро. Граф — очень хорошее представление в ситуации, когда нужно проложить маршрут из одного места в другое, как в нашем случае. Упрощенный граф облегчает составление маршрута по сравнению с максимально точной картой, где трудно выделить нужную информацию среди многочисленных подробностей.

Циклы

В информатике есть особое название для обхода графа, когда вы посещаете каждую вершину ровно один раз и возвращаетесь в начало. Это называется гамильтонов цикл — по имени ирландского физика Уильяма Роуэна Гамильтона. Он изобрел головоломку, по условиям которой нужно было обойти все углы додекаэдра, проходя по его граням.

Одно решение на двоих

Возвращаемся к началу

Возможно, вы уже заметили, что головоломка «Ход конем» и задача экскурсовода очень похожи друг на друга. Если вы записали требования для «Хода конем», то, вероятно, увидели полное совпадение.

1. Тур начинается в заданной точке.

2. Необходимо посетить все точки.

3. Нельзя проходить уже посещенную точку.

4. Необходимо закончить в начальной точке.

В обоих задачах вас просят найти гамильтонов цикл! Таким образом, мы использовали прием из вычислительного мышления. Мы обобщили обе задачи, чтобы они стали одинаковыми, и сделали это с помощью сопоставления с образцом, увидев важнейшие сходные черты. При этом мы абстрагировались от деталей, таких как отели и туристические достопримечательности или необходимость ходить конем или ехать по линиям метро.

Итак, задача экскурсовода оказалась легкой, потому что мы представили ее в виде графа. Так почему бы нам не сделать то же самое и с задачей «Ход конем»?

Для этого нужно абстрагироваться в большей степени. Чтобы это сделать, необходимо осознать две вещи. Во-первых, не важно, как выглядит доска. Не важно, что поля — это квадраты. Их форма и размер могли бы быть абсолютно любыми. Давайте нарисуем каждое поле в виде кружочка — так же, как достопримечательности изображены на карте метро. Это просто вершины графа.

Во-вторых, какие поля на самом деле находятся рядом друг с другом — тоже не очень важно. Единственное, что имеет значение, — между какими полями конь перемещается. Поэтому давайте соединим линиями любые два кружка, между которыми можно сделать ход. Подобным образом карта метро показывает, между какими достопримечательностями можно переместиться на метро. Это ребра графа.

Создаем граф

Чтобы сделать граф для головоломки «Ход конем», переходите с поля на поле и по мере продвижения рисуйте кружки и линии (вершины и ребра). Если четко выстроить путь, вы ничего не пропустите. Начните с поля 1. Нарисуйте кружок и пометьте его цифрой «1». Теперь с поля 1 можно перейти на поле 9 — значит нужно нарисовать еще один кружок, обозначить его как «9» и соединить их линиями. С поля 9 перейдите на поле 3 и нарисуйте еще один кружок, который пометьте «3» и соедините его линией с кружком 9.

Продолжайте так делать, пока не вернетесь к уже нарисованному кружку. Теперь отойдите на ход назад и попробуйте из этой точки пойти другой дорогой. Если других вариантов, которые вы еще не обозначили, больше нет, вернитесь еще на один ход и попробуйте оттуда. Продолжайте делать так до тех пор, пока не проведете эту операцию (она называется поиск с возвращением) до поля 1 и у вас не кончатся варианты. В итоге вы получите схему.

Заметим, что из трех внутренних кружков возможны только два хода, а значит, на завершенной схеме на каждую из этих вершин придется по два ребра (линии). С других полей можно сделать три разных хода, поэтому у их вершин будет по три ребра.

Идем вглубь

Способ исследования всех возможных ходов с целью нарисовать граф называется поиском в глубину: мы исследуем пути до самого конца, например продвигаясь через 1 — 9 — 3 — 11... до конца, потом сохраняем этот путь и пробуем другие. Альтернативный вариант (под названием поиск в ширину) подразумевает рисование всех ребер, исходящих из вершины, и всех вершин, к которым они ведут, перед перемещением к новой вершине. Используя этот метод, мы могли бы нарисовать все ребра из вершины 9, потом все ребра из вершины 6 — и так далее. Это два разных алгоритма для исчерпывающего исследования графа — два разных алгоритма обхода графа. Как только вы осознаете, что задачу можно представить в виде графа, то используйте любой из этих алгоритмов в качестве упорядоченного способа исследования графа и, соответственно, задачи.

Чистота и порядок

Если ваш рисунок получился немного беспорядочным из-за наезжающих друг на друга линий, как показано на рис. 34, можно перерисовать его начисто, чтобы линии не пересекались. В этом случае используйте два связанных шестиугольника — один внутри другого, как на рис. 35.

Когда вы аккуратно начертите граф, попробуйте снова решить задачу «Ход конем». Начните с вершины 1 и следуйте линиям, отмечая вершины, которые проходите. Теперь найти решение должно быть довольно легко.

Одна задача, одно решение

Теперь внимательно посмотрите на чистый вариант графа. Мы перечертили его, не меняя ребер и вершин, и он выглядит в точности как схема метро. Единственная разница — в обозначениях вершин. Цифры вместо названий.

Теперь видно, что эти задачи можно обобщить и что они не просто похожи, но в точности одинаковы. Если у вас есть решение для одной задачи (алгоритм, позволяющий найти ответ), значит, есть и для другой! Все, что нужно сделать, — поменять обозначения. Обобщенная версия алгоритма подойдет для обеих головоломок, и ничего не придется делать заново.

Сопоставление схем

На рис. 36 показано, как поменять обозначения на графе одной из наших задач, чтобы он подошел для другой. Еще на нем видно, как перевести решение одной задачи в решение другой. Обозначение каждого шага в алгоритме для одной из задач нужно заменить на соответствующее в другой.

Итак, если мы нашли следующее решение для задачи экскурсовода:

1. Отель.

2. Научный музей.

3. Магазин игрушек

4. Колесо обозрения.

5. Парк.

6. Зоопарк.

7. Аквариум.

8. Художественный музей.

9. Музей восковых фигур.

10. Военный корабль.

11. Замок.

12. Собор.

13. Отель,

то, используя таблицу, сразу же найдем решение для «Хода конем»:

1. Поле 1.

2. Поле 9.

3. Поле 3.

4. Поле 11.

5. Поле 5.

6. Поле 7.

7. Поле 12.

8. Поле 4.

9. Поле 10.

10. Поле 2.

11. Поле 8.

12. Поле 6.

13. Поле 1.

Эта таблица — еще один вид представления информации или структуры данных в виде таблицы поиска. С ее помощью вы легко найдете эквивалент поля из «Хода конем» в списке достопримечательностей из задачи для экскурсовода. Но стоит заметить, что искать поле, соответствующее достопримечательности, не очень удобно. Было бы гораздо лучше, если бы достопримечательности стояли в алфавитном порядке.

Схема для обеих задач

Схема на рис. 37 — еще одно представление той же информации, полученное методом наложения. Также она показывает единое решение (для обеих задач). Конечно, поскольку решений может быть много, вы можете прийти к какому-то другому, но и тогда оно подойдет для обеих задач.

Итак — вероятно, это удивит вас, — две разные вроде бы задачи оказались одинаковыми и с одним решением (после обобщения). Решив одну, вы сразу решили и другую! Это открытие происходит после выбора подходящих абстракций и подходящего представления двух задач (структура данных в виде графа).

Мосты Кенигсберга

Прогулка по городу мостов

Вот еще одна головоломка, над которой стоит поразмыслить. На рис. 38 показана карта города с рекой, протекающей через него, двумя островами и семью мостами через реку.

Туристический информационный центр хотел бы опубликовать маршрут прогулки по городу (оба берега и острова), чтобы по каждому мосту нужно было пройти один раз (не больше). Маршрут должен начинаться и заканчиваться в одном месте. Вас попросили проконсультировать центр — либо предложить маршрут, либо объяснить, почему он невозможен.

Похожую задачу о мостах города Кенигсберга в XVIII веке решил математик Леонард Эйлер. В своем решении он впервые ввел идею графов. В итоге они стали одним из ключевых вычислительных инструментов как в математике, так и в информатике. Ученые Викторианской эпохи Чарльз Беббидж и Ада Лавлейс, написавшие первые компьютерные программы, попытались решить ее в XIX веке. Нарисуйте граф для задачи и посмотрите, сможете ли решить ее, прежде чем читать дальше.

Мыслим логически

Вычислительное мышление подразумевает умение мыслить логически. Хорошее представление информации помогает в этом, потому что позволяет убрать ненужное и сосредоточиться на главном. Именно это и обнаружил Леонард Эйлер, когда решал задачу «Мосты Кенигсберга» и пришел к мысли нарисовать граф (рис. 39). Граф помог ему увидеть задачу предельно ясно.

Глядя на граф, Эйлер осознал, что найти ответ невозможно. Почему? Подходящий маршрут должен затронуть все вершины и обойти все ребра, но только один раз (поскольку ребра — это мосты, а нам сказали, что по каждому мосту можно пройти один раз). Давайте предположим, что такой маршрут существует, и, чтобы его показать, нарисуем пунктирные линии со стрелками вдоль ребер. Все ребра должны входить в маршрут, а значит, все они должны совпасть с пунктирными стрелками. Возьмем вершину на этом маршруте, как показано на рис. 40. На каждую пунктирную стрелку, направленную от нее, должна приходиться пунктирная стрелка, направленная к ней. В противном случае маршрут зайдет в тупик — когда пойдет по лишнему ребру, над которым не будет пунктирной стрелки. Из этого тупика не получится выйти без возвращения на уже пересеченный мост. То же относится и к любой вершине. Поэтому, чтобы искомый маршрут был возможен, у всех вершин должно быть четное число связанных с ними ребер.

Все вершины на графе Кенигсберга имеют нечетное число ребер, поэтому искомый маршрут невозможен. Однако со времен Эйлера через реку построили новый мост, поэтому граф изменился. Экскурсоводам современного Калининграда живется легче.

Собираемся и путешествуем

Настоящее путешествие

Мы рассмотрели простые головоломки с поиском маршрута. Теперь возьмем задачу из реальной жизни. Представьте, что специалист по продажам каждый день настраивает навигатор, чтобы найти самый короткий путь, позволяющий по одному разу посетить несколько клиентов в разных городах и снова оказаться в офисе, не возвращаясь по собственным следам.

Такую кратчайшую дорогу можно просчитать, но вряд ли получится каждый раз делать это за разумный промежуток времени. Даже если надо побывать у 20 клиентов, нельзя гарантировать, что вы ежедневно будете находить оптимальное решение — на это потребуется слишком много времени. И дело не в том, что требуется более мощный навигатор или компьютер. Если число мест, где необходимо побывать, достаточно велико (на самом деле оно не очень-то и велико), то на поиск совершенного решения уйдет больше времени, чем прошло с момента возникновения Вселенной, — даже при наличии самого быстрого компьютера! Почему? Потому что число возможных вариантов, которые необходимо проверить, стремительно растет с появлением каждого нового города. Даже если навигатор запрограммировать на какое-то решение, нельзя гарантировать, что оно будет безупречным. Заложенный в программу способ не обеспечит кратчайшего пути. Вполне вероятно, что в программе сработает так называемый жадный алгоритм. Давайте изменим условия задачи, чтобы понять, о чем идет речь.

Пакуем чемоданы

Представьте, что вы отправляетесь в долгий отпуск, мечтая хорошо отдохнуть. Открытый чемодан лежит на кровати. Вы уже упаковали одежду и теперь собираете вещи, которые хотите взять с собой, — книги, настольные игры, пазлы, колоду карт, краски и бумагу… Все, что, по вашему мнению, поможет расслабиться. Все эти вещи разного размера. Их нужно сложить в чемодан. Как это сделать? Пробуем разные варианты. Сначала пазл, потом игральные карты, потом книга с кроссвордами — и так далее. Если у вас достаточно места, то все получится, однако, если места маловато или вы не хотите брать много чемоданов, намечается проблема.

Хорошей альтернативой будет жадный алгоритм. С его помощью не получится упаковать все максимально компактно, но порой он работает весьма хорошо. Как выбрать, что положить сначала? Исходите из жадности. Положите самый большой предмет внутрь, пусть он займет как можно больше места. Теперь положите следующий по размеру — и так далее. Если что-то не помещается, берите следующий чемодан. Обычно все получается само собой, потому что, когда у вас остаются небольшие свободные пространства, вы заполняете их небольшими предметами. Это годный эвристический алгоритм — с такими алгоритмами вы достаточно хорошо (но не безупречно) справитесь с задачей. Они не гарантируют оптимального решения.

Снова в дороге

Основная идея жадного алгоритма применима и при разработке маршрута для коммивояжера. Используя ту же идею обобщения, вы на каждом этапе выбираете ближайший к точке отправления город. При этом не всегда получается оптимальный вариант, но можно рассчитывать на хороший результат за разумное время.

Хороший, плохой, злой

Идея прокладывания маршрута между точками, которая при подходящем обобщении дает граф, возникает снова и снова при решении самых разных задач. Как только вы осознали, что это граф, в вашем распоряжении сразу оказывается много алгоритмов. Тогда некоторые задачи оказываются легкими, а другие — нерешаемыми. Однако интереснее всего те, что по мере роста масштаба задачи утрачивают рациональность решения. В этом случае необходимо правильно подать информацию и выбрать алгоритм. К примеру, важно вовремя заметить, что проблема становится сложной и лучше использовать эвристический алгоритм.

Выбор подачи информации и алгоритма может быть хорошим или плохим. Некоторые варианты подачи и алгоритмов просто красивы — их элегантность доставляет настоящее удовольствие в процессе решения задачи.

Глава 6
Создание бота. Руководство для начинающих

Теперь, ознакомившись с основами вычислительного мышления, рассмотрим, как с его помощью создать искусственный разум для робота. Строить тело робота интересно, но без «мозга» оно ни на что не способно. Мы изучим историю роботостроения, выясним, что такое «понимать», и создадим систему искусственного интеллекта — виртуального собеседника, или чат-бота.

У роботов своя история

Недоброе имя?

Термин «робот» впервые появился в пьесе R.U.R. («Россумские универсальные роботы») чешского писателя-публициста Карела Чапека. В этой пьесе на заводе, расположенном на уединенном острове, делают человекоподобных роботов, «труд которых в пять раз дешевле человеческого». По ходу действия разворачивается знакомый сюжет, который заканчивается тем, что (подумать только!) все люди, за исключением одного, погибают во время восстания роботов. В финале последний человек совершает акт самопожертвования и заставляет двух роботов полюбить друг друга. Занавес.

Считается, что в пьесе отразилась озабоченность Чапека тоталитарным обществом, которую он выразил в виде научной фантастики. Отсюда и мрачный сюжет. Если бы автор оказался в иной политической ситуации, то появление роботов в информационном пространстве могло бы быть не таким зловещим. Это подчеркивает тот факт, что выбранное Чапеком слово «робот» происходит от чешского robota, означающего «рабский труд». Сначала Чапек хотел назвать этих существ laboři (от латинского labor — «работать»), но передумал и попросил совета у брата Йозефа. Йозеф предложил использовать слово robota. Братья Чапеки создали обоснование и название для роботов как раз тогда, когда в западном мире появились технологии, которые впоследствии привели к их созданию.

Что такое робот в вашем понимании?

У всех нас разные представления о том, что делает робота роботом. Однако в самом простом смысле робот — это машина, действия которой управляются программой. Мы склонны представлять роботов как больших размеров механических работников, которые постепенно завоевывают мир. Но стиральная машина на кухне тоже робот. Она управляется компьютером, не страдает мегаломанией, а стирает белье с разной скоростью и при разной температуре. Так что «роботы» действуют только на основе программного обеспечения. Это могут быть программы, которые действуют в цифровом мире — например, изображают виртуальных персонажей в видеоиграх, по крупицам собирают данные с сайтов, создавая новые знания, или управляют компьютерами, зараженными вирусами. Таких виртуальных роботов называют ботами, и, хотя у них нет физического тела, они выполняют необходимые функции.

Давайте кратко рассмотрим историю материальных роботов, а потом перейдем к самому интересному — как создать искусственный разум.

Были и выдумки

Истории о механических роботах с древних времен присутствуют во всемирной истории. В трактате «Ле-цзы» описывается человекообразный робот, созданный в Китае в III в. мастером Яньши для чжоуского царя Му. Это была полноразмерная фигура человека, сделанная из кожи, дерева и искусственных органов. В мифологии Древнего Крита есть персонаж по имени Талос — бронзовый витязь, который охранял остров, подаренный Европе, от пиратов. А в еврейских преданиях рассказывается о големах — глиняных великанах, которые оживают и выполняют указания по записке, вложенной им в рот.

Все это — интересные истории, но на практике одним из первых конструкторов и создателей роботов был Герон Александрийский, древнегреческий математик и изобретатель, который строил автоматы, приводимые в движение сжатым воздухом, паром и водой. Считается, что в XIII в. инженер Аль-Джазари описал программируемый человекообразный автомат в «Книге знаний об остроумных механических устройствах» (1206 г.). Это была лодка с четырьмя музыкантами, которая плавала по озеру и развлекала гостей. Мелодию можно было менять, перемещая деревянные колышки на вращающемся барабане, отчего ударные инструменты играли в разное время.

Появление заводных автоматов, изощренных механических кукол, служивших развлечением для европейских дворов в XVIII в., впоследствии привело к созданию электронных роботов. Благодаря работам ученого Уильяма Грея Уолтера, пионера кибернетики (науки о том, как животные и машины контролируют свое поведение), мы стали осознавать как полезность роботов, так и сложность их создания.

Сегодня у нас дома помимо стиральных машин есть и другие роботы. Возможно, у кого-то из ваших знакомых есть робот-пылесос, который убирает дом в отсутствие хозяев, робот-газонокосильщик или автомобиль, который умеет парковаться. Современные самолеты оснащены автопилотом и умеют взлетать и приземляться самостоятельно. Если вы когда-нибудь летели в отпуск и в точке назначения был сильный туман, скорее всего, командир доверил посадку автопилоту. Почему? Потому что так безопаснее. Подобным образом беспилотные автомобили обычно безопаснее автомобилей, управляемых водителем-человеком. Так роботы начинают входить в нашу жизнь, и они достаточно «умны», чтобы научиться делать работу лучше нас, демонстрируя более мощный искусственный интеллект (ИИ).

Как создать «разум» для робота

Создаем послойно

Создание искусственного интеллекта действительно интересная задача. Как же это сделать? Разные типы информации обрабатываются в разных участках мозга, но неким образом сводятся в рабочее целое. С этой проблемой сталкиваются создатели роботов и систем ИИ. Простейший вариант «мозга» робота довольно примитивен: это электронная схема, которая заставляет робота беспорядочно двигаться. Следующий этап — наделить его способностью реагировать на происходящее кругом.

На практике строить простые машины, которые воспринимают мир и реагируют на него так же, как простейшие формы жизни, несложно. Например, схема такого робота при регистрации громкого звука может реверсировать электродвигатель. Другой робот останавливается при наступлении темноты. Третий, оснащенный солнечной батареей, может двигаться в направлении яркого света, чтобы перезарядиться (то есть «поесть»). Роботы могут регистрировать присутствие других роботов и стараться держаться ближе друг к другу.

Конечно же, у робота иное представление о мире, которое зависит от типа сенсоров. Например, мы можем построить робота, который «видит» благодаря эхолокатору, подобно летучей мыши, издающей ультразвук, слышит эхо от окружающих предметов и изменяет направление полета, огибая объекты на своем пути.

Если взять все эти компоненты, каждый из которых представляет собой очень простой способ реагирования на мир, и объединить их, то возникнут интересные и более сложные проявления: например, роботы, которые ищут источник энергии, но прячутся в темном месте при первом намеке на опасность. Каждый компонент создается отдельно, а потом мы объединяем их в более сложное целое. Это метод декомпозиции, используемый в вычислительном мышлении, который применяется при конструировании роботов с целью получить комплексное поведение, как у животных.

Робототехник Родни Брукс придумал простой способ осуществления этой идеи. Его предикативная архитектура похожа на слоеный пирог. Каждый слой при активации вызывает разное поведение — например, бесцельное перемещение или реагирование на свет. Действия, которые запускаются нижними слоями, включаются в более высокий слой (используются или поглощаются) при активации поведения, соответствующего этому слою. Это вариант абстракции в сочетании с декомпозицией.

Более сложные системы контроля над роботами (верхние слои) могут обеспечить некое элементарное внутреннее представление о мире. Например, они «знают» (используя алгоритм для сопоставления с образцом), какую последовательность действий и в каком порядке стоит запустить, когда в мире робота возникает конкретная ситуация — например, раздался сигнал тревоги.

Иногда с системой ИИ или роботизированной системой случается непредвиденное и она начинает вести себя иначе, чем запланировал создатель. Серия простых действий, запущенных в определенном порядке, приводит к возникновению неопределенного поведения: роботы начинают совершать не предусмотренные для них действия. Например, программа Boids имитирует простые правила полета птиц — демонстрирует движение примерном в том же направлении, что и любые птицы рядом, но не допускает сближения с соседями. Благодаря этим простым правилам получается элегантная имитация полета настоящей птичьей стаи.

Естественно отобранные

Итак, мы посмотрели, как непосредственно создают роботов с разумным поведением. Есть и другой способ: создать искусственный разум с помощью процесса, напоминающего эволюцию путем естественного обора. Естественный отбор основан на выживании наиболее приспособленных, как если бы каждое поколение детей участвовало в гонке на выживание. Только если они будут успешны в гонке на выживание, они вырастут и смогут завести собственных детей (рис. 41). Родители передают детям качества, которые их самих привели к успеху, но из-за скрещивания и мутаций дети не являются точной копией родителей, и в гонке на выживание они проявляют себя лучше или хуже. Дети соревнуются друг с другом. В каждом поколении выживают только те, кто успешно выступает в гонке, и постепенно популяция становится все больше приспособленной к выживанию. Конечно же, в реальной жизни это скорее непрерывный процесс, а не серия раундов.

Вычислительное моделирование этого естественного процесса привело к появлению новых способов производить вычисления и писать программы. Создается начальное количество возможных вариантов, и каждый из них проходит испытание на годность,обычно с помощью компьютерной симуляции. Затем отдельные решения ранжируются по результатам. Самые эффективные сохраняются, но потом в них случайным образом вносят простые изменения — например, обменивают их свойства на качества других «выживших» и таким образом получают «детей» следующего поколения. Остальные варианты отбрасываются. Так продолжается в течение многих тысяч поколений. Компьютер снова и снова тестирует варианты, пока не появляется чемпион, который гораздо лучше справляется с работой, чем те, от кого он произошел.

Учиться себя вести

Еще один способ создать искусственный разум — написать программу, которая может учиться. Потом ей нужно показать множество примеров желаемого поведения в разных ситуациях. Понемногу она будет тренироваться на примерах и сможет освоить нужные действия по шаблонам. Разновидность этого способа — позволить машине учиться на своих ошибках. «Наказывать» ее, когда она делает что-то неправильно, и «вознаграждать», когда все хорошо. В этом случае ПО приспосабливается повторять хорошее поведение и избегать плохого и постепенно все чаще и чаще ведет себя так, как нам хотелось бы. Подробнее мы рассмотрим это в следующей главе.

Как бы ни компоновался ИИ — был ли он создан разработчиками-людьми, обучался ли какому-то поведению на многочисленных примерах или эволюционировал путем выживания наиболее приспособленных, — у него почти гарантированно будет модульное устройство. Компоненты с разным поведением объединяются для выполнения задачи — это декомпозиция. Такой подход позволяет отдельно тестировать каждый модуль и повторно использовать их в других, более новых системах, что упрощает и удешевляет производство роботов. Также это означает, что по мере усовершенствования индивидуальных компонентов и появления новых будут создаваться еще более сложные ИИ, поскольку мы всё лучше понимаем каждую конкретную возможность.

Создаем своего виртуального собеседника

Поговорим о чат-ботах

Способность говорить — один из фундаментальных признаков человека, поэтому, чтобы понять, как применить вычислительное мышление к ИИ, можно начать с посещения психотерапевта. Но в нашем случае в роли психотерапевта выступит компьютерная программа под названием «Элиза», которую в середине 1960-х гг. написал Джозеф Вейценбаум в Массачусетском технологическом институте. Это был первый виртуальный собеседник, созданный, чтобы вести обычную беседу с человеком. Люди разговаривали с «Элизой», полагая, что общаются с настоящим психотерапевтом. Вейценбаум назвал ее в честь Элизы Дулитл — цветочницы-кокни из пьесы «Пигмалион», которую учат разговаривать как люди из высшего общества, это была своего рода шутка для посвященных. Программа одной из первых прошла тест Тьюринга — одно из самых известных и авторитетных испытаний для ИИ — на умение вести беседу.

Человек ли я?

Тест Тьюринга основан на следующем положении: если мы не видим разницы между навыками ИИ и человека, в данном случае это навык поддерживать разговор, — это значит, что ИИ прошел тест и должен считаться таким же разумным, как человек. Разработал этот тест математик, криптограф и информатик Алан Тьюринг, который, предположительно, позаимствовал идею из викторианской салонной игры. По правилам этой игры из комнаты выходят мужчина и женщина, а остальные придумывают для них вопросы. Вопросы записывают на карточках и передают их вышедшей паре. Те пишут ответы и передают их обратно. Играющие зачитывают ответы вслух и пытаются догадаться, кто автор. Сложность в том, что мужчине разрешается лгать, а женщина обязана говорить правду (викторианцы, предположительно, считали, что женщинам не пристало врать, мужчинам же…). Если мужчине удастся убедить играющих, что он женщина, то он побеждает. В противном случае выигрывает женщина.

Тьюринг осознал, что надо сделать нечто похожее с компьютером. Он предложил поместить в одну комнату не мужчину и женщину, а машину и человека и дать им похожее задание — выяснить, кто из них машина, просто задавая вопросы. Как и мужчине в салонной игре, компьютеру разрешается как угодно вас обманывать. Тьюринг утверждал, что если после долгого разговора невозможно заметить разницу, то надо признать, что машина обладает таким же интеллектом, как и человек.

Вейценбаум решил, что беседа с «Элизой» должна имитировать диалог с психотерапевтом, потому что в такой ситуации допускается нечеткость формулировок и смена тем и таким образом повышается вероятность обмана.

Моделируем разговор

В сущности, «Элиза» была простой вычислительной моделью работы психотерапевта и в более общем смысле — диалогов между людьми. Сначала, чтобы узнать конкретные слова и фразы во введенном тексте, ей надо было проводить сопоставление с образцом. Потом она использовала эти подсказки, чтобы выбрать из списка шаблонных исходящих фраз или правил действия, имеющие смысл в этом контексте. Например, если вы упоминали во входящей фразе мать, «Элиза» опознавала это слово и могла выдать фразу «Расскажите больше о вашем раннем детстве».

Таким образом, перед создателем робота стоит задача создать библиотеку условных конструкций «ЕСЛИ x, ТО y», заменяя x и y подходящими естественными фразами, имеющими отношение к ситуации. В целом за этими правилами стоит та же идея, которую мы выдвинули для решения логических головоломок, однако в данном случае решается задача убедительно провести беседу с человеком. Если получится ее решить, то возникнет иллюзия понимания. «Элиза» показала, что этого на удивление легко добиться с помощью простой программы, особенно в том, что касается коротких разговоров. Основные элементы «Элизы» до сих пор присутствуют во многих виртуальных собеседниках.

Тем не менее можно ли считать компьютер, прошедший тест Тьюринга, таким же разумным, как человек, — вопрос спорный. Вернемся к салонной игре. Даже если мужчина убедил всех, что он женщина, это не значит, что он действительно женщина — просто он хорошо притворяется. Подобным образом, если компьютер проходит тест Тьюринга, значит, он хорошо изображает разумность. Однако, создавая модели, которые становятся все более убедительными, мы можем проверить и лучше понять структуру человеческого общения, а также лучше узнать, что мы подразумеваем под разумностью.

Создаем виртуального собеседника

Вы можете сделать собственного виртуального собеседника — и даже без компьютера. Понадобятся только чистые карточки, ручка, ну и надо подумать немного. Во-первых, решите, на какую тему пойдет беседа. Это может быть все что угодно, но в первый раз лучше сосредоточиться на хорошо известных вам вопросах — например, на любимом виде спорта или телесериале, потому что вам легко представить осмысленный разговор на эту тему. Послушайте настоящие диалоги о выбранном вопросе и отметьте, что говорят люди. Затем вам понадобится подключить алгоритмическое мышление. Нужно будет придумать набор ключевых слов, которые робот должен узнать в разговоре, а также отклики на них. Потребуется алгоритм беседы. Например, ваш чат-бот без ума от футбола и его собеседник упоминает «штрафной» (ключевое слово). На это робот отвечает: «О! Бэкхем отлично бил штрафные. Вы не пробовали навесить как Бэкхем?» Возможно, вам придут в голову идеи получше, и сложится более естественный диалог. Задавать вопросы, как «Элиза», — хорошая мысль, потому что в этом случае собеседник делает основную работу. Чтобы разговор был реалистичным, нужно найти много ключевых слов и соответствующих реакций. Вероятно, вам будет легче, если разговор пойдет на узкую тему — по крайней мере поначалу. Например, об одной футбольной команде, а не о футболе вообще. Еще потребуются нейтральные фразы, которые вы будете использовать, если не удается провести сопоставление с образцом, — помните, что алгоритмическое мышление подразумевает составление инструкций для всех возможных вариантов! Однако такие реакции не должны повторяться, поэтому нужен целый набор нейтральных фраз.

На карточках из первой группы напишите ключевые слова, которые виртуальный собеседник будет искать в разговоре. Это наш вводимый текст. Пронумеруйте карточки. Теперь расположите их в алфавитном порядке и соедините скрепкой. Например, первые карточки на футбольную тему могут быть такими, как на рис. 42, хотя вам, конечно, понадобится значительно больше ключевых слов.

На карточках из второй группы напишите предложения, которые послужат ответами, — выводимые фразы. Пронумеруйте их в соответствии с ключевыми словами, которые будут их запускать. Скрепите и эти карточки, но на сей раз в порядке нумерации. На рис. 43 представлены образцы ответов на приведенные ключевые слова.

Если разложить карточки в таком порядке, чат-боту будет легче работать. Как только поступит вводимый текст, вы просмотрите ключевые слова, разложенные по алфавиту, сразу найдете соответствующее число и возьмете нужную карточку с выводимым текстом. Так вы создали легкое в использовании представление для правил вашего чат-бота.

Эти правила необходимо оценить. Когда закончите, дайте карточки другу, и пусть он сыграет роль компьютера, на котором запущена программа-бот. Поговорите с ним. Друг должен следовать указаниям на картах и вести обычную беседу. Убедителен ли ваш чат-бот? Смог бы он одурачить вас? Попросите еще одного друга поговорить с ним и ответить на эти вопросы. А теперь попробуйте провести беседу в текстовой форме и не признавайтесь, что участник эксперимента беседует с роботом!

Попросите друзей оценить вашего чат-бота — например, по шкале от 0 до 5. Каковы его слабые и сильные стороны? Что нужно улучшить? Что выдало робота? Отзывы помогут понять, какие карточки с ответами нужно заменить и что добавить.

Ответ на такие вопросы — это еще один пример оценки пользователем. Как мы уже говорили, программисты всегда оценивают, насколько успешно их программы справляются с поставленной целью. Оценка — важная часть вычислительного мышления. Возьмите идеи, полученные в ходе оценки пользователей, и усовершенствуйте устройство чат-бота и ваши фразы. Повысятся ли оценки при повторном тестировании? Если нет, то почему? Если вы умеете программировать, то, получив некоторый опыт в составлении убедительных диалогов с чат-ботом, напишите соответствующую программу.

Сегодня создатели виртуальных собеседников не склонны имитировать психотерапевтов. Их роботы пытаются, например, изображать молодых иностранцев, которые объясняют, почему в программе произошел сбой, или собирают как можно больше настоящих реплик, чтобы брать из них образцы для сопоставления. Часто виртуальных собеседников создают не программисты, а люди, у которых хорошо получается создавать убедительные персонажи. Они используют специальные обобщенные программы для создания чат-ботов, которые наполняют разговорными элементами. Если у вас хорошо получается создавать такие персонажи, попробуйте заняться этим профессионально и населять ими виртуальные миры.

Следует ли опасаться ботов?

Чат-боты появились как эксперимент в программировании и психологии. Сейчас это — приложения, которые находят самое разное практическое применение. Например, персонажи, с которыми можно встречаться в виртуальных мирах, игрушки, которые хотят быть вашими друзьями, замена человеку в контакт-центрах и даже личные ассистенты, такие как дворецкий Джарвис у супергероя Железного человека.

Однако у чат-ботов есть и темная сторона. Порой они имитируют людей по гораздо менее достойным причинам. Рост социальных медиа привел к тому, что присутствие чат-ботов ощущается по всему миру. Эксперименты показали, что в соцсетях роботов часто признают за людей и они собирают тысячи подписчиков. Бывали даже случаи, когда политические активисты использовали чат-ботов, чтобы повлиять на политические взгляды людей с внешним эффектом естественного изменения общественного мнения. Это явление получило название «астротерфинг». Но если с помощью роботов удается изменить политические убеждения, значит, можно повлиять и на результаты выборов. Такие явления подрывают демократию. И это лишь одна из многих юридических и этических проблем, связанных с законным использованием ИИ и роботов, которые до сих пор не исследованы. Особенно важны процессы, развива­ющиеся в интернете. Мы склонны думать, что интернет населен людьми, но опрос 2014 г. показал, что около 60% трафика в нем создают роботы.

Интересно, что бы сказала об этом «Элиза»?

Понимает ли вас виртуальный собеседник?

Входим в китайскую комнату

Системы, построенные на порождающем правиле «ЕСЛИ — ТО», как наш чат-бот, могут выполнять сложные операции, которые имитируют деятельность человеческого мозга в конкретных обстоятельствах. Конечно же, настоящий вызов здесь — создать ИИ или робота, который справится со всем, с чем справляется человек, а не будет выбирать единицы информации, что полегче. Способность видеть, слышать и чувствовать мир с высокой скоростью и точностью, общаться письменно и устно, влюбляться, писать музыкальные хиты или быстро принимать разумные решения, когда значительная часть информации неизвестна или неточна, — все это позволяет нам выживать в нашем сложном мире. Кроме того, мы, люди, понимаем, чтó мы делаем, в отличие от многих ИИ, для которых это является проблемой. ИИ следует правилам, но не понимает.

Философ Джон Сёрл показал эту проблему в мысленном эксперименте под названием китайская комната. Представьте, что вы совсем не знаете китайского языка — не пишете и не говорите на нем, и оказались в запертой комнате, где есть книги с правилами перевода с китайского языка. Через щель в двери вы получаете сообщения от носителей китайского. Вы ищете в книгах нужные правила, касающиеся написанного, действуете в соответствии с ними, а потом просовываете результат обратно в щель. Вы поступаете в точности как виртуальный собеседник, который следует правилам о том, что нужно «говорить» в ответ на полученные сообщения. Носители языка за дверью получают осмысленные ответы на свои вопросы, написанные на китайском. Значит, сама комната или что-то внутри нее понимает китайский, не так ли? Но вы знаете, что всего лишь следовали сложному набору правил, которые дают результат. Вы не понимаете ни ответы, ни вопросы. Так «понимает» ли китайский комната и находящийся в ней человек? Или она просто симулирует способность понимать по-китайски? Сёрл называет первый вариант сильным ИИ, а второй — слабым ИИ. Большинство людей сказало бы, что комната ничего не понимает. Все понимание имеется у людей, которые придумали правила. Этот мысленный эксперимент и поднятые им важные вопросы о природе понимания вызвали массу споров в среде философов и программистов. Попробуем переиначить его на свой лад.

Клингонская комната

Многие люди владеют азами китайского языка, а значит, не подходят для участия в этом мысленном эксперименте. Кроме того, китайский — «мудреный» язык, на котором говорят миллионы. Он развивался веками и отличается особенным построением фраз и набором исключений. Это живой естественный язык огромного масштаба и сложности. Было бы очень трудно создать правила, необходимые для описанного эксперимента, и это несколько его обесценивает. Давайте выберем более простые и реалистичные условия.

Говорите ли вы по-клингонски? Для мысленного эксперимента подойдет любой язык, который понимает хоть кто-нибудь. Клингонский — это пример нового языка с собственной лексикой, грамматикой и алфавитом, который создал Марк Окранд, отдав дань миру научно-фантастического сериала «Звездный путь». В нашем случае он выступит в роли полезной и более простой альтернативы китайскому. Это язык с синтетическим синтаксисом: нам с самого начала точно известны грамматические правила составления предложений. Мы точно знаем, как был создан этот язык, каковы его правила и синтаксис, его семантика (значение слов и предложений) и то, как в нем работают глаголы и существительные. На этом внеземном языке бегло говорят некоторые люди. Из этого легко вывести, что написать книги по переводу с клингонского для нашей комнаты реально. В особенности потому, что мы точно знаем, чтó можно выразить на этом языке. В основном, и это неудивительно, на нем говорят о борьбе, чести и космических кораблях. Например, слово, обозначающее «капитанский мостик» космического корабля, появилось на ранних этапах. И лишь много лет спустя в язык вошло понятие о «мосте» как способе перейти водную преграду. Это довольно экстремальный искусственный пример эволюции семантики — смыслового значения единиц языка и того, как возникает общее понимание значения слова. В настоящих человеческих языках такой процесс часто занимает столетия, и его трудно отследить.

Очевидно, что создать клингонскую комнату можно. Так поймет ли человек, находящийся в ней и ничего не знающий об этом языке, вопросы на клингонском, если будет отвечать так же, как в китайской комнате?

Поворот сюжета

Давайте изменим условия, чтобы создать собственный мысленный эксперимент. Возьмем одну китайскую комнату, где вопросы за дверью задают китайцы, и одну клингонскую комнату, где вопросы задают самые знающие фанаты. Будут ли люди у дверей китайской комнаты ощущать, что она хуже понимает их язык, потому что книги с правилами перевода было очень трудно написать и не всегда удалось в точности передать детали (да и можно ли зафиксировать все нюансы настоящего живого языка)? Будут ли наши «клингонцы», чья картина мира изобилует понятиями, связанными с честью и борьбой, чувствовать, что их комната дает более качественные ответы, потому что ей нужно освоить гораздо меньшие объемы? Если это так, то, возможно, дело в том, что в книгах с правилами перевода должны быть учтены все значения (семантика), а также все слова и грамматика (синтаксис). Значит ли это, что, если бы мы создали достаточно уточняющих правил, охватывающих весь реальный мир, комнаты обрели бы способность понимать?

Как вы думаете?

Глава 7
Создаем мозг

Мы не будем пытаться сразу же сконструировать интеллект, но, используя вычислительное мышление, начнем создавать простой мозг постепенно и с нуля. Это поможет нам изучить, как на самом деле работает человеческий мозг, состоящий из множества связанных между собой нервных клеток, и как формируется наше сложное поведение. В итоге мы начнем понимать, как создать искусственный интеллект, который не просто ведет себя как человек, а делает это, потому что его мозг работает похожим образом. Возможно, что, если получится точно воссоздать мозг, в нем зародится интеллект.

Создаем обучающийся мозг

Искусственный интеллект учится играть в карты

Мы уже знаем, что компьютеры слепо выполняют написанные для них инструкции — алгоритмы. В этом их сила, но трудно утверждать, что компьютеры разумны. Наш интеллект проявляется не только в способности решить конкретные задачи, но и в гибкости. Мы учимся. Они — нет. Обучение — ключевой элемент интеллекта, но как будет учиться искусственный интеллект, если он всегда следует инструкциям? Выходит, нужно создать алгоритм для обучения!

Давайте начнем с действительно простого задания для ИИ — проверить, получил ли он необходимое число монет. Сформулируем задачу точнее. Чему именно должен научиться наш простой ИИ? Допустим, нам нужно, чтобы он смог сообщить, когда у него есть две монеты — но только если это действительно так. Если монет нет или на столе только одна монета, делать ничего не надо. Будем считать, что у ИИ есть сенсор для монет, однако нужно научиться их считать.

Чтобы объяснить, как в этом случае происходит обучение, мы используем простую версию самообучающейся машины. Для этого понадобится игровое поле, показанное на рис. 44, и набор карт (не важно, что на них изображено). Сыграв серию раундов этой игры, машина научится правильно определять, есть ли у нее нужное число монет. Игроки кладут (или не кладут) монету на игровое поле, после этого карты перемещают по столу, складывают и сравнивают числа. В итоге машина выдает ответ.

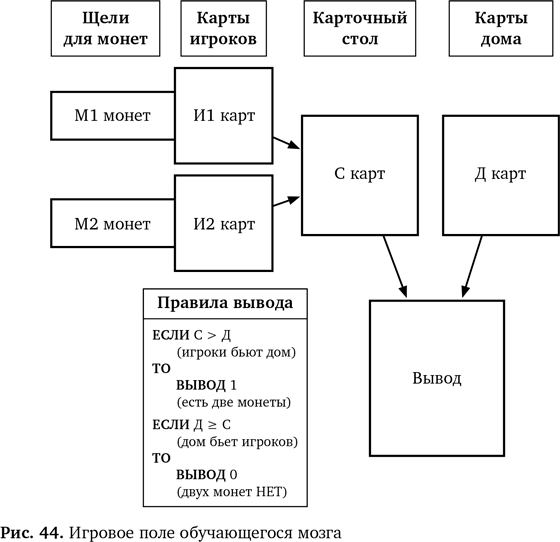
У машины есть две щели, куда каждый из двух игроков помещает монеты, чтобы их посчитали. Карты обоих игроков выкладываются в нужную позицию на поле. Еще есть зона карточного стола, где играют в карты, и зона, куда складывают карты дома. Итоговую карту раунда кладут в последнюю зону — зону выхода. Выбирают из двух итоговых карт, на одной стоит 0, а на второй — 1.

Игра идет слева направо следующим образом. Мы сдаем небольшое произвольное число карт двум игрокам и дому — это, соответственно, И1, И2 и Д. Потом мы играем серию раундов. Каждый игрок должен положить монету в щель, чтобы получить право сыграть раунд. Сделав это, игроки открывают карты — И1 и И2. Эти карты отправляются в зону карточного стола (там они складываются, и мы получаем сумму — С). Сумма играет против дома. Если у игроков больше карт, чем у дома (С > Д), то они выиграли. В этой ситуации выход равен 1. Нам нужно, чтобы в конечном итоге это означало «Есть две монеты». Если выигрывает дом, то выход равен 0, и мы надеемся, что это будет означать «Двух монет НЕТ». В любом случае карты игроков отправляются в начальную точку и начинается следующий раунд.

Поскольку мы сдаем произвольное количество карт и оно определяет результат, мозг настольной игры тоже будет действовать произвольно. Нам необходимо, чтобы после многократного повторения игры наш мозг научился менять изначальное случайное число карт на число, которое всегда дает нужный результат. То есть в конце выход должен быть равен 1, только если присутствует две монеты. Результат, которого мы хотим добиться, представлен на рис. 45.

Машина учится это делать в ходе серии раундов, и после каждого раунда мы применяем следующие простые порождающие правила, где М1 обозначает число монет, которое положил игрок 1 (одну монету или ни одной), а М2 — число монет, которое положил игрок 2.

Правило П1:

ЕСЛИ сыгранная партия дает правильный выход,

ТО не делайте ничего — не меняйте число карт.

Правило П2:

ЕСЛИ сыгранная партия дает на выходе 1, но мы хотели получить 0, чтобы это соответствовало таблице выходов,

ТО заберите М1 карт у игрока 1 и М2 карт у игрока 2.

Правило П3:

ЕСЛИ сыгранная партия дает на выходе 0, но мы хотели получить 1,

ТО добавьте М1 карт игроку 1 и М2 карт игроку 2.

Эти правила — обучающий алгоритм для нашего мозга. Пора оценить их, поэтому давайте посмотрим на примеры.

Пример игры 1. Удачный расклад, все хорошо!

Представим, что сейчас в игре три карты, сданные игроку 1, четыре — игроку 2 и три — дому (И1 = 3, И2 = 4, Д = 5). В щели 1 есть монета (М1 = 1), а в щели 2 монеты нет (М2 = 0). Мы запишем, что (М1, М2) = (1, 0).

Поскольку в щели 1 есть монета (М1 равно 1), то три карты И1 выкладываются на стол, а карты И2 — не выкладываются, потому что М2 равно 0. Соответственно, на карточном столе у нас три карты (рис. 46).

Можно обобщить количество карт (С), которое отправляется на стол. Оно вычисляется с помощью уравнения:

С = ((М1 × И1) + (М2 × И2)).

В нашем примере получается (1 × 3 + 0 × 4) = (3 + 0) = 3. Из операции умножения следует, что значения М1 и М2 определяют, будут ли сложены соответствующие суммы. Если М равно 0, то значение И не учитывается в сумме, а если оно равно 1, то значение остается.

Таким образом, сумма С для нашего мозга равна 3, и это меньше, чем Д, равное 5 (3 < 5), поэтому карта, помеченная как 0, помещается в зону выхода: «Двух монет НЕТ». Это выход, который мы хотим получить, когда в игре только одна монета. В этом случае мы применяем правило П1 и ничего не делаем.

Теперь попробуем другой вариант. Все карты возвращаются туда, откуда они взяты. Однако на этот раз давайте поместим по монете в обе щели: (М1, М2) = (1, 1). Теперь карты обоих игроков идут на стол, поскольку в обеих щелях есть монеты. И остается семь карт: (1 × 3 + 1 × 4) = 7.

Теперь 7 > 5, и на выходе 1, как нам и нужно: «Есть две монеты». И снова мы следуем правилу П1 и не делаем ничего.

Более того, если мы попробуем все четыре комбинации монет в щелях, то каждая из них даст правильный выход. Ура! Обучения не потребовалось. Но в данном случае нам повезло. Нам случайно сдали столько карт (три, четыре и пять), что машина сработала правильно. С таким количеством карт она всегда может правильно сказать, присутствуют две монеты или нет. Но что будет, если не повезет? Тогда придется играть по-другому и учиться необходимому поведению. Давайте рассмотрим другую игру.

Пример игры 2. Нужно играть

Мы снова начинаем с того, что произвольно сдаем игрокам и дому небольшое количество карт. На этот раз у игрока 1 на столе шесть карт, у игрока 2 — четыре карты, и у дома тоже четыре карты.

Ситуация, когда ни в одной щели нет монет, а значит, М1 и М2 равны 0, легкая. Карты не перемещаются, для дома мы получаем 0 < 4, и на выходе 0: «Двух монет НЕТ». Условие (М1, М2) = (0, 0) корректно. Это показано на рис. 47.

Если монета есть только в щели 2, значит, (М1, М2) = (0, 1). Тогда карты игрока 2 идут вперед. Игрок 1 остается на месте, и на стол попадают четыре карты. На выходе мы имеем 0: «Двух монет НЕТ». Помните, что для получения 1 на выходе нам нужно, чтобы сумма карт на столе была больше (а не просто равна) Д. То есть ничего не меняется, и мы снова следуем правилу П1. Условие (М1, М2) = (0, 1) корректно.

Теперь поместите одну монету в щель М1 и ни одной — в щель М2. И снова мы хотим получить на выходе 0, однако посмотрите на карты! На карточном столе у нас 6 ≥ 4, а значит, на выходе 1, и это неверно! Нужно применить правило П2. В нем говорится:

«ЕСЛИ сыгранная партия дает на выходе 1, но мы хотели получить 0, чтобы это соответствовало таблице выходов,

ТО заберите М1 карт у игрока 1 и М2 карт у игрока 2».

Это значит, что, поскольку М1 равно 1 и М2 равно 0, мы забираем карту у игрока 1, но не забираем у игрока 2. Новое значение И1 — 5 (6 − 1), а И2 остается равно 4.

Забрав карту из стопки игрока 1, мы возвращаем его карты. Мы не забрали ни одной карты игрока 2. Машина начала учиться.

Теперь мы выбираем другое условие и пробуем еще раз. Экспериментируя с этим примером, вы вернетесь к (М1, М2) = (1, 0), проходя через возможные вводные, и снова получите ошибку. И снова будет применено правило П2, и машина наберется еще немного опыта. На этот раз, когда карту убирают у И1, получается 4.

На этом этапе И1 = 4, И2 = 4, Д = 4. Итак, когда та же ситуация повторится снова, все получится, потому что в игре четыре карты игрока и четыре карты дома. Выход для (М1, М2) = (1, 0) будет 0: «Двух монет НЕТ», а это нам и нужно. Вы также обнаружите, что случай (М1, М2) = (1, 1) тоже дает верный результат. При этом условии конечное уменьшенное значение И1(4) + И2(4) = 8. У дома 4, а 8 > 4.

Наша машина научилась действовать правильно только благодаря игре и меняла карты, когда у нее не получалось. Правила игры — обучающий алгоритм.

Минус не помеха

Поэкспериментируйте с игрой сами. Вы обнаружите, что в какой-то момент придется применить все правила П1–П3 в зависимости от того, какие карты сданы в начале игры. Это поможет машине усвоить правильное поведение. Оно зависит от того, с чего вы начнете, и от порядка, в каком вы будете опускать монеты в щели (разные условия), но в конце концов даст результат. Если по правилам игры требуется взять карт больше, чем осталось у вас на руках, вы прибегаете к старой доброй «долговой расписке». Напишите записку c текстом «–1 карта» или «–2 карты» и продолжайте играть, проверяя, получите ли вы правильный ответ для каждого из условий. В конце останутся значения И1 и И2, которые будут соответствовать либо картам на руках, либо расписке, но игра все равно будет выучена.

Чем полезна игра с мозгом?

В этой игре вы создали самообучающийся модуль для мозга, чтобы вычислять логическую функцию «И». Он учится сообщать, есть ли монеты в щели 1 и в щели 2. Однако мы не программировали логическую функцию «И» — модуль сам научился ее вычислять. Использованный здесь принцип обучения основан на идее нейронной сети.

Нейронная сеть имитирует (моделирует) вычислительные операции мозга на базовом уровне — это абстракция. Миллиарды нервных клеток мозга, называемые нейронами,можно рассматривать как простые устройства обработки данных. Они связаны с другими нейронами с помощью особых отростков аксонов и получают сигналы из других частей нейронного контура. Если сигнал, поступивший в часть клетки, называемую синапс, достаточно силен (превышает весовой порог нейрона), то этот нейрон отправляет сигнал к другим, соединенным с ним.

Наша настольная игра моделирует один-единственный нейрон. В роли вводных сигналов используются монеты. Мы хотим, чтобы сигнал проходил (выход 1), только если присутствуют оба вводных сигнала (например, в обеих щелях есть по монете). Карты на руках представляют собой нейронный вес. Это меняющиеся элементы нейрона, которые помогают ему учиться. Количество карт, сданных дому, действует как весовой порог нейрона. Сначала нейроны не знают, как складывать поступающие сигналы. Они включаются случайно, подобно случайному числу карт, сданных в начале игры. Нейронные веса могут находиться где угодно. Но как один нейрон-кирпичик поймет, что делает мозг в целом? Ему необходимо учиться — и это делается по тому же принципу, что и в нашей карточной игре. Нейроны получают сигнал, который сообщает, был выход верным или неверным (поэтому весь процесс называют контролируемым обучением), и соответствующим образом меняют веса, укрепляя одни связи и ослабляя другие. При этом используются правила обучения, похожие на наши порождающие правила П1, П2 и П3. Веса, определяющие взаимосвязи, могут быть положительными (как карты на руках) или отрицательными (как «долговые расписки»).

Наша игра создает вычислительную модель работы нейронов. Мы сделали алгоритмическую версию нейронов, которая при симуляции действительно ведет себя нужным образом. Мы использовали игру с настоящими предметами, но то же самое можно сделать и с помощью программного обеспечения, которое создает модели с тысячами и даже миллионами нейронов. Такие модели позволяют исследовать, верно ли мы понимаем поведение нейронов. Будет ли наша модель вести себя как простой мозг?

Булевы операции

Итак, мы разобрались с биологическим обучением. Но что такое упомянутая логическая функция «И»? Это пример булевой операции. Булевы операции можно представить в виде таблиц (рис. 45) с булевыми значениями ИСТИНА (1) и ЛОЖЬ (0), на которых основана логика. Их в XIX в. разработал математик Джордж Буль. Математические способности этого удивительного человека позволили ему в 19 лет открыть собственную школу в Линкольне. Сделав блестящую карьеру, он неожиданно умер в возрасте 49 лет. Однажды Буль прошел больше двух миль под проливным дождем и стал читать лекцию прямо в мокрой одежде. Неудивительно, что у него начался сильный жар. К несчастью, жена математика Мэри, которая незадолго до этого уверовала в гомеопатию, решила лечить его средствами, «подобными причине болезни». Она стала поливать его водой из ведра прямо в постели. Стоит ли говорить, что состояние Буля ухудшилось, и 8 декабря 1864 г. он умер.

Работа Буля заложила основы для идеи логических вентилей, которые мы до сих пор используем в цифровых электронных схемах. В кремнии каждого микропроцессора сделаны миллионы логических вентилей, которые могут быстро вычислять сложные суммы. Точнее говоря, из кремния сделаны транзисторы, но конструктору трудно ориентироваться на них при создании новых разработок. Поэтому транзисторы группируют в логические вентили. Создавая логические вентили И (срабатывает, если на ввод подаются оба сигнала), ИЛИ (срабатывает, если есть хотя бы один сигнал) и так далее, конструктор думает о них и забывает о транзисторах — их можно игнорировать. Это обеспечивает первый уровень абстракции в создании цифровой электроники.

Логические вентили группируются в компоненты, которые делают более сложные операции — например, складывают и умножают, перемещают данные из точки в точку. Эти функции обеспечивают еще более высокий уровень абстракции. Конструктору больше не нужно думать о логических вентилях, он может рассуждать в терминах этих изощренных функций. Вообще, создатели микросхем используют много уровней абстракции, переходя все выше по мере того, как усложняется дизайн. Если посмотреть на это с другой стороны, можно увидеть здесь пример декомпозиции. Чтобы создать вычислительное устройство, нам нужны суммирующие и множащие элементы — и так далее. Но как сделать суммирующий элемент? Для этого необходимы логические вентили. Как их сделать? Из транзисторов. Современные микросхемы сложнее, чем дорожная сеть всей планеты. Чтобы их сконструировать, необходимо использовать вычислительное мышление в грандиозных масштабах.

Логические вентили не обязательно делать из транзисторов. Как мы видели, их можно создать из простых нейронных контуров. Если заменить логические вентили на основе транзисторов эквивалентами на основе нейронов, результат будет аналогичным. Исследователи в лабораториях электроники и вычислительной техники по всему миру исследуют возможности биокомпьютинга. Например, они наблюдают, как меняется пульсация в нейронных контурах с течением времени, и размышляют, как учесть это в быстрообучающихся кремниевых или германиевых микросхемах. Алгоритмическое мышление работает в обе стороны. Оно не только позволяет заниматься научными исследованиями — порой алгоритмические версии природных процессов помогают найти новые способы работы компьютеров.

Наша простая схема подсчета монет, которая учится правильно выполнять задачу с нуля, делает тривиальные операции. Но если такую схему объединить с миллионами похожих для совместной работы, можно создать огромную вычислительную армию. Конечно, самое сложное — запрограммировать ее. Нужно разработать необходимое программное обеспечение, и все они будут вместе работать над общей целью.

Играем в «Снап!» с нейронной сетью

Не так просто, как кажется

Наша игра с проверкой монет была не слишком интересной. Давайте сыграем в настоящую игру — например, «Снап!». Если две карты совпадают, кричите «Снап!». Если они разные, молчите. Чтобы упростить процесс, будем считать, что у нас есть только красные и черные карты. Получится ли создать нейронную сеть, чтобы сыграть в эту игру?

Давайте разберем, как именно наша нейронная сеть будет определять совпадение цветов. Пусть 1 означает карту красного цвета, а 0 — черного. Красный–красный (1, 1) или черный–черный (0, 0) — это «Снап!», красный–черный (1, 0) или черный–красный (0, 1) — нет. Процесс похож на проверку монет с помощью И, но не так прост в освоении.

Цветной «Снап!» — это пример использования функции исключающее ИЛИ. Она немного похоже на функцию И, но активизируется, только если на входе (1, 0) или (0, 1), — и ни в каких иных случаях. Функция активизируется, только если истине соответствует один сигнал (то есть один сигнал равен 1), но не оба, как на рис. 48.

На заре нейронных сетей такого рода логика представляла собой большую проблему. Нейронные контуры, которые тогда назывались перцептронами, отлично работали с И, ИЛИ и с другими простыми операциями в булевой логике, но не могли справиться с досадным моментом исключения. Причина состояла в их геометрии. Оказалось, что перцептрон работал, создавая границу решения — линию на графе. При достаточном сигнале на вводе перцептрон переходил через границу. Это зависело от весов и порогов восприятия в контуре (наши значения И1, И2 и Д в предыдущей игре). Пока явления, для которых мы хотели получить разный выход, были по разные стороны границы решения, все было хорошо — перцептрон работал.

Но в случае с функцией «исключающее ИЛИ», где нам нужна линия в соответствии с таблицей на рис. 48, ничего не получилось. Если изобразить это на графе с использованием данных координат (где красный — 1, а черный — 0), то окажется, что на выходе невозможно отделить ответы, равные 0, от ответов, равных 1. Нельзя создать систему, в которой, когда вас толкают через границу, одно состояние сменяется другим (см. рис. 49).

И вот идея: если каждый перцептрон может нарисовать только одну линию, нужно использовать больше перцептронов. Если один перцептрон будет питать другой и получится так называемый многослойный перцептрон, то каждый слой будет определять линию решения и мы сможем использовать две линии.

Можно ли его сделать?

Да, сделать его можно. Есть несколько способов создать нейронные контуры, которые могут работать с исключающим ИЛИ или играть в «Снап!», и на рис. 50 представлен один из таких способов. Заметим, что здесь мы используем представление в виде графа, чтобы показать нейронный контур. В конечном итоге главное здесь — нейроны и их взаимосвязи. Еще мы абстрагируемся от внутренних подробностей работы нейронов и сосредотачиваемся на их усвоенном поведении.

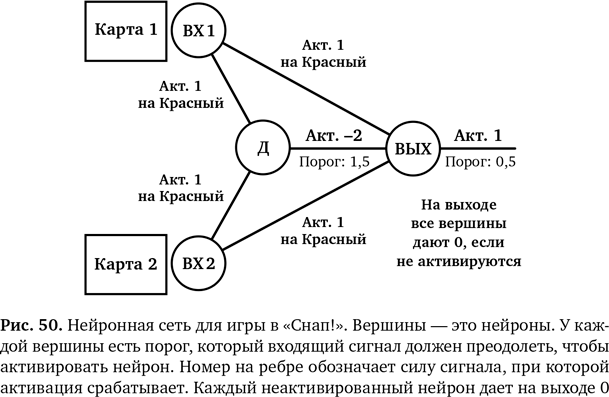
Теперь у нас есть нейронная сеть из четырех взаимосвязанных нейронов. У нас два нейрона на входе — ВХ1 и ВХ2, которые определяют цвет видимых ими карт. Они дадут на выходе 1, если карта красная, и 0 — если черная. Этот результат идет в нейрон Д (дом) во втором слое. Порог для его активации — 1,5 (то есть он активируется при условии, что сумма сигналов на входе больше 1,5), но сам он дает на выходе отрицательный результат (−2). Все сигналы поступают в третий нейрон, ВЫХ с порогом 0,5.

Эту схему нужно проверить. Давайте пройдемся по всем комбинациям.

Комбинация (черный, черный) дает на выходе 0

Если на входе поступает комбинация (0, 0), это (черный, черный), и нейрон во втором слое, Д, получает сигнал 0 с обеих сторон (см. рис. 51a). Для Д сигнал 0 меньше, чем порог 1,5, поэтому вершина Д активирует 0. Сигналы, поступающие на нейрон ВЫХ, суммируются (0 + 0 + 0), и на выходе Д дает 0. Это меньше, чем порог 0,5 для нейрона ВЫХ, поэтому он не активируется, и перцептрон на выходе дает 0.

Комбинация (красный, красный) дает на выходе 0

Комбинация (красный, красный) дает на вход в нейрон Д (1, 1), в сумме 2. Это больше, чем 1,5, поэтому Д активируется и дает на выходе –2. На ВЫХ у нас есть сигналы, поступающие напрямую со слоев входа, 1 и 1, поэтому их надо добавить к взвешенному сигналу –2 от Д: (1 + 1 + (–2)). В сумме получается 0, и это меньше, чем порог для ВЫХ, поэтому на выходе получается 0 (рис. 51b).

Комбинация (черный, красный) дает на выходе 1

Если на вход поступает сочетание (0, 1), то есть (черный, красный), то Д получает только 1, что меньше его порога, поэтому Д не активируется. На ВЫХ мы получаем 0 от ВХ1, поскольку на входе черный, и 1 от ВХ2, потому что на другом входе — красный. Они суммируются с 0 на Д (0 + 1 + 0) и дают 1. Это больше, чем 0,5, поэтому на выходе происходит активация — ВЫХ выдает 1 (см. рис. 52a).

Комбинация (красный, черный) дает на выходе 1

Рассмотрите последний случай, где на входе (1, 0), то есть (красный, черный), и вы увидите, что на ВЫХ будет 1, как на рис. 52b.

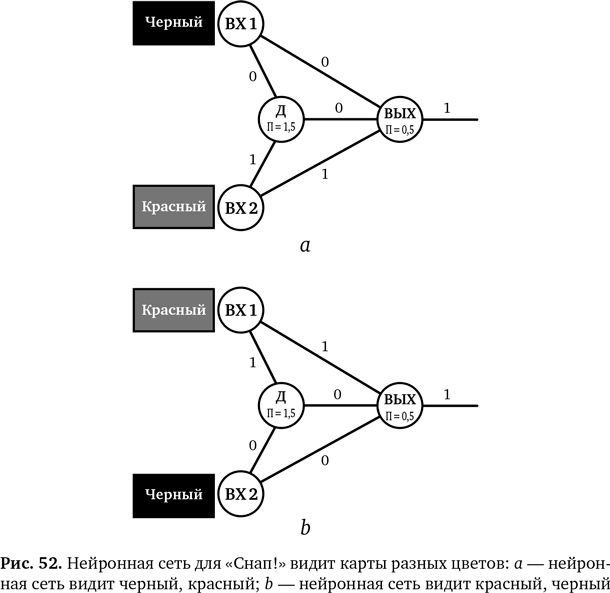
В целом эта закономерность сочетаний на входе и на выходе соответствует таблице для исключающего ИЛИ. А чтобы правильно играть в нашу игру, нужна именно она. Таким образом, мы создали элементы мозга, которые умеют играть в цветной «Снап!».

Мне квалиа и чашку синего кофе, пожалуйста

В предыдущей главе мы рассмотрели вопрос, способны ли чат-боты понимать. Теперь мы увидели, что можно создавать мозг из искусственных нейронов. Давайте примем в расчет эти нейроны и посмотрим на вопрос понимания под другим углом. Человеческие существа понимают, у них есть сознание, и они воспринимают квалиа. Квалиа — термин, относящийся к нашему внутреннему опыту и восприятию. Возьмем, например, вкус кофе или синеву ясного неба. Все мы знаем, что это такое, но как объяснить это другому? Что такое «кофейность» или «синева»? Если принять, что сознание определяется мозгом (есть исследователи, которые так не считают), тогда нечто в проявлениях нейронов и мозговых структур порождает поведение и простые действия, возникновение смысла, квалиа и даже такие чувства, как любовь. Если точно смоделировать важные для создания этого внутреннего опыта части мозга, то, возможно, наш искусственный мозг тоже их испытает — и квалиа в том числе. Здесь нужно правильно провести абстрагирование и создать модель для всех этих частей мозга, опуская только не имеющие большого значения. Но найти и выделить их — огромная задача для нейронауки и информатики.

В то же время мы начинаем понимать, что активная работа нашего мозга ведется все-таки не нейронами. Есть и другие клетки, которые, вероятно, обрабатывают информацию, и другие действующие в мозге нейромедиаторы, которые влияют на работу этих клеток.

Разные типы информации отбираются для обработки в разных частях мозга, но каким-то образом все это объединяется, чтобы дать нам... собственно, нас самих и наше понимание мира. Но если мы посмотрим на один нейрон, скажем, в миндалевидном теле — участке мозга, который по идее порождает эмоции, то увидим, что он просто или возбуждается, или нет в зависимости от силы поступающего электрохимического сигнала. Он не понимает, что на более общем уровне вносит свой вклад в возникновении у индивида чувства страха. Это просто переключатель, и он просто переключает.

Даже при наличии новых технологий так называемого глубокого обучения, когда значительный рост доступной вычислительной мощности и новые математические алгоритмы позволяют программировать нейроны на многих уровнях, чтобы они решали полезные задачи вроде разработки новых лекарств, тегирования изображений и предсказания погоды или ситуации на фондовом рынке, мы до сих пор не понимаем, как в мозге формируются многие наши человеческие характеристики. Есть исследователи, которых интересует, как со временем меняется характер мозговой активности. Они создали хитроумные электронные схемы под названием импульсные нейроны, которые посылают последовательности электронных импульсов, имитируя возбуждение и расслабление настоящих нейронов. Эти ученые надеются, что, изучив зависящие от времени свойства этих систем, они смогут лучше понять работу мозга и создать новые приложения. Очевидно, что для понимания работы мозга абсолютно необходимо правильное абстрагирование, и хотя в этой области был достигнут значительный прогресс, она по-прежнему остается волнующим исследованием Неизвестного.

Изучение человеческого мозга и поведения, а также сравнение их с искусственным интеллектом все еще требуют ответа на глубокие философские вопросы. Однако, располагая компьютерами с искусственным разумом, мы можем использовать их для исследования этих глубоких вопросов, которые подводят нас к самой сути человеческого, ну и по ходу дела создавать полезные инструменты и программы, которые помогают нам в жизни. У вас будут собственные соображения по этим вопросам — и они тоже будут верными. В конце концов, вы человек.

Глава 8
Делаем робота-мошенника

Мы рассмотрели основные принципы создания мозга и виртуального собеседника — и знаем, что некоторые из них перешли на Темную сторону вычислительных систем. Теперь давайте все это объединим. Пора рассмотреть вопрос, как создать простейшего бота, который будет дурачить людей. В результате мы поймем, почему те, кто владеет вычислительным мышлением, — будь то люди или компьютеры — должны иметь представление об этике. Роботы появились на сцене с «мыслью» о мировом господстве, поэтому мы рассмотрим, почему им никогда не удастся управлять миром.

Разум-предсказатель

Автомат, способный на мистификацию

После короткого экскурса в тайны человеческого мозга не помешает создать загадочный и зловредный искусственный интеллект, чтобы исследовать другие аспекты робототехники и искусственного разума.

Сейчас мы займемся созданием ИИ, который сыграет роль псевдогадалки — конечно же, исключительно в образовательных целях. Таким образом мы увидим, как вычислительное мышление позволяет дурачить людей. Для нашей аферы понадобится несколько хитрых объединенных вместе элементов. Нужно придумать основную мошенническую схему, привлечь клиентов, убедиться, что клиент передал деньги, и узнать, совпал ли цвет у перевернутых карт. Давайте по очереди рассмотрим все эти этапы.

Удача любит смелых

Представьте себе такую сцену. В полутемной комнате витают экзотические ароматы. В сумраке видны странные символы и необычные рукописи о давно забытых магических искусствах. На столе — кристаллы, осколки загадочных былых времен. Почти незаметно появляется предсказательница, искусственный интеллект. Она предлагает вам сесть. Сеанс начинается.

«Добро пожаловать. Кристаллы сказали мне, что сегодня твои вибрации особенно восприимчивы. Я слышу зов судьбы. Твоя аура говорит, что ты чуткий и жизнерадостный человек, но бывали времена, когда жизнь тебя не радовала. Возможно, это были страдания от неудовлетворенности собой. Ты знаешь, что у тебя есть скрытые способности, которые ты пока не использовал на благо другим и себе, как хотелось бы. Ты знаешь: чтобы произошел прогресс, нужно достичь гармонии с другими, но и не предать себя.

Я могу помочь. Всего за две монеты я могу найти в колоде твою уникальную карту. Если носить ее с собой, она будет символизировать и указывать дорогу, которая приведет к гармонии и принесет удачу.

Я чувствую твои сомнения. Я должна подтвердить, что слияние энергий произошло и что контакт установлен в нужной мере. Чтобы это проверить, тебе необходимо добровольно выбрать карту из колоды. Если цвета карт, выбранных тобой и мной, совпадут, это подтвердит контакт. Если я потерплю неудачу, то заплачу тебе неустойку. Ты получишь назад три монеты — одной я искуплю прискорбную ошибку в моем предсказании.

Хочешь, чтобы карты показали будущее? Ты точно ничего не потеряешь и, возможно, многое приобретешь!»

Сеанс заканчивается… дважды

Первый вариант: вы платите две монеты, предсказательница выбирает удачную карту, а потом вы берете случайную карту из колоды. Цвета совпадают — обе карты красные. Контакт есть. Затем вам предсказывают будущее по картам, и вы выходите из комнаты, а предсказательница, явно утомленная соединением нитей судьбы, кладет монеты в карман и тихо покидает комнату.

Второй вариант: вы платите две монеты, вам показывают удачную карту, вы выбираете вторую, но, к сожалению, цвета не совпадают — выпали красная и черная. Обещанный контакт не подтвержден. Предсказательница приносит извинения: тонкий план сегодня рассинхронизирован. Вам дают обещанные три монеты — две ваших и еще одну в качестве компенсации за разочарование. Гадалка извиняется. Возможно, получится в следующий раз, но и сейчас вы скорее приобрели, чем потеряли. Выходя из комнаты, вы богаче, чем были, когда вошли. И, может быть, уже подумываете зайти в другой раз, когда знамения будут благоприятными.

Каким бы ни был финал, все это — мошенничество с целью наживы, но как оно работает? С виду все честно. Но почему люди ловятся на такие схемы в реальности?

Схема аферы

В чем же обман? Давайте посмотрим, как загадочная математика превращает вроде бы честную схему в принципиально мошенническую. За аферой стоит простая математическая ошибка, которую делают люди, чью бдительность усыпили образ предсказательницы и сценарий диалога (подробнее о нем ниже). Посмотрим на математическую подоплеку. Если наша искусственная гадалка выбирает удачную карту нужного цвета, ей достаются две монеты. Если у нее не получается, она платит три монеты. Этот штраф кажется приличным вознаграждением, пока вы не вспоминаете, что две из этих монет вы сами отдали за предсказание. Таким образом, если карты не совпадают, ИИ теряет только одну монету.

Здравый смысл подсказывает, что нужно рассмотреть вероятность обоих исходов. Удачная карта, по сути, ерунда, это просто любая карта, взятая из полной колоды. Тестовая карта — еще одна случайная карта из оставшейся колоды. То есть это все равно что играть в цветной «Снап!» с полной перетасованной колодой. Шанс, что две карты совпадут по цвету (выпадут черная с черной или красная с красной), равен шансу, что карты не совпадут по цвету (выпадут красная с черной или черная с красной). Это шанс 50 : 50.

Если наш ИИ-псевдогадалка повторит эту схему несколько раз, то начнет получать деньги. Почему? Представьте, что у него появится 10 жертв. В среднем, сыграв 10 раз, 50% (пять человек) отыграют деньги, потому что карты не совпадут, однако 50% (пять человек) уйдут без наличности. На рис. 53 эта ситуация обобщена.

Чем больше людей сыграет, тем больше сможет получить мошенник-ИИ. Сделать ошибку довольно легко. Мы не видим, какие математические последствия повлекут наши действия в долгосрочной перспективе. Такие вещи происходят часто, и не только в случае мошенничества. Например, парадокс дня рождения: как это ни удивительно, если в одном помещении соберутся всего лишь 23 человека, шанс, что у двоих совпадет день рождения, равен 50%.

Поймаем их на Барнума

Теперь мы знаем, как устроена наша мошенническая схема. Но как заставить людей на нее купиться? Если не вдаваться в подробности, хватит убедительной математики. Если нечего терять, значит, нет причин не вступить в игру. Но есть и другие способы, которые помогут нам привлечь клиентов. В шестой главе мы говорили о виртуальном собеседнике— это системы ИИ, способные имитировать разговор. Они работают в беседах на общие темы, но можно ли создать с их помощью интерфейс для взаимодействия с клиентом, который будет таким же убедительным, как гадалка?

У нас должно сразу сложиться впечатление, что виртуальный собеседник умеет предсказывать, — еще до того, как он предложит вытащить удачную карту. Но как псевдогадалке завоевать доверие? Для этого пригодятся так называемые утверждения Барнума, которые применяют, чтобы вызвать доверие, манипулируя нашим восприятием языка. Они названы в честь знаменитого циркового антрепренера Финеаса Барнума,который прославился своими мистификациями. Эффект Барнума основан на том, что люди склонны видеть точное описания себя в утверждениях, которые на самом деле применимы к большим группам, например «порой вы сомневаетесь в сделанном выборе» или «некоторые ваши сны очень далеки от реальности». Да уж! Конечно, они подходят всем, но в ходе экспериментов участники указывали, что именно эти утверждения относятся непосредственно к ним. Диалог с нашей ИИ-гадалкой с самого начала строится с использованием утверждений Барнума. То есть в разговоре фигурируют только обобщения, но мы обрабатываем их смысл таким образом, что нам кажется, будто ИИ обладает неким глубоким и мистическим знанием о нас. Так нас втягивают в аферу со счастливой картой.

Как и любой виртуальный собеседник, наш тоже может вести более сложный диалог. Необязательно следовать точному сценарию. Можно на выбор взять набор утверждений Барнума. Это может быть случайный выбор, или же робот будет реагировать на высказывания жертвы с помощью наиболее подходящих утверждений Барнума, и тогда получится убедительнее. Вы, как создатель, сами определяете уровень сложности.

Строим шаг за шагом

Итак, у нас есть убедительная мошенническая схема и бот, который будет привлекать игроков и заставлять их расставаться с деньгами. Чтобы создать ИИ, который сможет целиком провернуть эту аферу, необходимы еще два элемента. Система должна проверять, действительно ли игрок отдал деньги. В противном случае может выясниться, что она сама стала жертвой обмана — радостно раздавала деньги, но ничего не брала себе! Ей нужно уметь проверять, положила ли жертва две монеты на стол. Но этот элемент мы уже создали — мы просто возьмем одну обученную нейронную сеть из главы 7.

Кроме того, нам нужно, чтобы она понимала, когда брать деньги, а когда платить. Для этого она должна проверять, действительно ли две выбранные карты одного цвета. Этот элемент мы тоже уже создали! Нам потребуется другая нейронная сеть из главы 7 — та, которая умеет играть в цветной «Снап!».

Вот так, объединив старые и модифицированные компоненты, мы сделаем робота-мошенника. Это обычный чат-бот, работающий с утверждениями Барнума, наш счетчик монет, обученный необходимым действиям, и система, играющая в «Снап!», — только она не будет кричать «Снап!», а займется проверкой карт.

Мы снова использовали декомпозицию. Каждая часть создавалась со своей целью, но с помощью некоторого обобщения отдельные модели можно свести вместе, чтобы создать нечто новое.

Этика и мировое господство

Создание ИИ, добро и зло

Этот пример показывает, как создать работающую систему ИИ, объединив различные компоненты: чат-бот с утверждениями Барнума, счетчик монет и игрока в цветной «Снап!». Вообще, каждый из этих элементов можно создать из обычных предметов, которые найдутся дома, — карт, бумаги, ручек и монет. Для создания ИИ необязательно пользоваться компьютером, ведь вычисления производят разными способами. Конечно же, можно закодировать различные компоненты, абстрактные понятия и алгоритмы в виде программы, которая будет работать на компьютере. Но стоит ли заполнять мир ИИ, которые вот так обманывают людей?

Мы использовали этот пример, чтобы объяснить, как работают вычислительные элементы, такие как сопоставление с образцом, обработка языка, нейронные системы и порождающие правила «ЕСЛИ–ТО», но специалисты по компьютерным наукам, которые создают реальные вычислительные системы, должны учитывать в своей работе этические моменты. Какие блага обеспечивают их системы и кому? Есть ли типы ИИ, которые не стоит создавать, и почему? Насколько допустимо манипулировать людьми, которые пользуются этими системами? Например, допустимо ли создавать системы, которые имитируют людей, чтобы обмануть, вызвать зависимость или каким-то образом навредить? Эти вопросы рассматриваются в этике, которая изучает, что плохо и что хорошо с точки зрения морали и нравственности. Разработчики ИИ должны соблюдать закон, однако некоторые явления законны, но в то же время приносят вред. Можно ли отнести ИИ-гадалку к такого рода явлениям? Что по этому поводу думаете вы и ваши друзья? Вычислительные системы существуют в обществе, и необходимо, чтобы они соответствовали его нормам, а будущие создатели ИИ должны это учитывать.

Главный вопрос… завладеют ли роботы миром?

С того момента, как в 1921 г. была напечатана пьеса R.U.R., о которой мы говорили несколько глав назад, и в языке возник термин «робот», непрерывно появляются фильмы и телесериалы о роботах или ИИ, которые пытаются завладеть миром. Но какое отношение злонамеренные ИИ из фильмов имеют к научной реальности? Может ли ИИ завладеть миром? Каким образом он это сделает? И зачем ему это? Все, кто придумывает кино­злодеев, должны продумать предпосылки, без которых не обходится ни один сюжет, — мотивы и возможности.

Ищем подходящий мотив

Давайте рассмотрим возможные мотивы. Вряд ли кто-нибудь считает, что интеллект как таковой обязательно ведет к желанию завоевать мир. Если вы сдали школьные экзамены, значит ли это, что вы автоматически встали на путь зла? Конечно, нет. В фильмах ИИ часто действуют из соображений самосохранения — они понимают, что испуганные люди могут их отключить. Но зачем создавать у наших инструментов ощущение, что они находятся под угрозой? Они обеспечивают нам разные блага, и, кроме того, зачем наделять самосознанием систему, которая, например, ищет в интернете ближайший итальянский ресторан?

Еще один популярный мотив для злодеяний искусственного интеллекта — рьяное следование логике. Например, такой сюжет: защитить Землю можно, только истребив все человечество. Это уничтожение из соображений логики напоминает представление, в соответствии с которым компьютер предпочтет остановившиеся часы опаздывающим на две секунды, потому что в первом случае часы показывают точное время два раза в день, а во втором — никогда. Такое обоснование сюжета, основанное на сомнительной логике в сочетании с пренебрежением к жизни, судя по всему, не согласуется с современными системами ИИ, которые в условиях неопределенности рассуждают математически и рассчитаны на безопасное взаимодействие с людьми. Айзек Азимов, один из классиков научной фантастики, продумал этот момент в сборнике рассказов о роботах «Я, робот». Там во всех роботов встроен неизменимый кодекс, «три закона роботехники», которые не дают им вредить человечеству.

Шанс стучится в дверь

Когда мы предполагаем, что ИИ теоретически может завоевать мир, для этого есть более веские основания. Известный тест Тьюринга для искусственного интеллекта был придуман, чтобы оценить конкретную способность — умение вести правдоподобную беседу. Предполагалось, что если нельзя увидеть разницу между собеседником-ИИ и человеком, то ИИ прошел тест и должен считаться таким же разумным, как человек.

Как же будет выглядеть тест Тьюринга, который обнаружит «способность» завоевать мир? Чтобы ответить на этот вопрос, нужно сравнить антисоциальные проявления ИИ с качествами потенциального властелина из числа людей. Завоевателям мира необходимо контролировать все важные сферы жизни — например, доступ к деньгам или возможность купить дом. ИИ делают это уже сейчас: например, решение о предоставлении кредита часто принимает ИИ, который просеивает горы информации, чтобы определить вашу платежеспособность. Кроме того, ИИ сейчас торгует на фондовом рынке.

Властелин мира будет отдавать приказы и ждать, чтобы их выполняли. Всякий, кто в беспомощности стоял у кассы самообслуживания, которая непрерывно требовала положить товар в пакет или убрать его оттуда, знает, что значит оказаться под властью ИИ.

Бинго «Мировое господство»

Давайте сыграем в тематическое бинго, чтобы узнать, насколько ИИ приблизился к завоеванию мира. Для этого нужно сделать собственные карточки. Нарисуйте на каждой сетку, например 3 на 3, и в каждой клетке напишите качество, необходимое для мирового господства. Например, вспомните, как действует ваш любимый суперзлодей. Что предпримет новый властелин мира? Может быть, возьмет интернет под контроль? Лишит людей свободы передвижения? Или даже займется сбором налогов? Заполните карточку, указав по одному из злодейских действий в каждой клетке. Поменяйтесь с другом.

Правила просты. Продвигаясь против часовой стрелки, ищите в интернете примеры того, что роботы или системы искусственного интеллекта делают то, что указано у вас в карточке. Найдите как можно больше вариантов. Когда найдете пример, запишите, на каком веб-сайте он описан, и вычеркните его. Постарайтесь отыскать подтверждения для примеров, которые заполнят сетку по вертикали или по горизонтали, как в обычном бинго.

Первый, кто заполнит строку или столбик, кричит «Бинго!» (конечно же, голосом злого робота) и выигрывает. Но прежде чем закончить, проверьте, какие действия вычеркнуты и какие примеры, описанные на веб-страницах, им соответствуют. Если время ограничено, победит игрок, который вычеркнет максимум действий, но опять-таки убедитесь, что эти примеры реальны и что они соответствуют действиям суперзлодеев на карточках.

Играя в эту игру, вы получите более полное представление о том, на что действительно способны сегодняшние роботы и ИИ. А потом можно либо начинать беспокоиться, либо почувствовать себя в безопасности.

Убить Билла?

Ни один голливудский робот с манией величия не обходится без хоть какого-то желания убивать. У нас уже есть дроны, созданные для убийства. Военные роботы могут определять цель без вмешательства людей. Сейчас команду атаковать дает управляющий ими человек, но вполне можно утверждать, что у этого ИИ есть потенциал убивать по своей воле. Но чтобы это стало возможно, придется изменить программный код. Впрочем, автономные роботы-убийцы уже существуют, хотя убивают и не людей. Пока мы пишем эти строки, в район Большого Барьерного рифа завозят роботов, которые будут выслеживать и убивать ядом морских звезд, разрушающих кораллы. Этим автоматам не потребуется приказ человека — оказавшись на свободе, они будут сами решать, кто умрет, а кто останется в живых.

Возможно, эти примеры подтверждают, что ИИ контролирует ограниченные, хотя и важные сферы жизни на Земле. Но чтобы действительно завоевать мир, как в кино, отдельным системам ИИ придется действовать вместе и объединиться в синхронизированную армию. Властолюбивому автомату, который пробивает ваши покупки на кассе самообслуживания, чтобы помешать вам купить пиво, придется связаться с датчиком здоровья. Затем они оба могут вступить в сговор с системой, подсчитывающей кредитный рейтинг, и она пообещает повысить кредитный лимит, если вы купите кроссовки со встроенным датчиком GPS и будете есть только зеленый салат из умного холодильника. Конечно, холодильник будет открываться, только если от кроссовок поступят данные о завершении обязательной семикилометровой пробежки.

Это тревожная картина, но, к счастью, она маловероятна. Разработчики по всему миру создают интернет вещей — сеть, объединяющую самые разные приборы и физические объекты, с помощью которой можно предлагать новые услуги. Чтобы завоевать мир, многочисленным кусочкам пазла нужно объединиться и образовать полную картину. Такая ситуация не очень вероятна — слишком много компонентов должно совпасть и одновременно сработать. Похоже на пресловутое противоречие в сюжете «Дня независимости», когда Apple Mac подключается к кораблю инопланетян. Поразительная межплатформенная совместимость.

Наши земные системы ИИ, созданные с помощью различных языков программирования, по-разному хранят разные данные и используют разные и несовместимые наборы правил и техники обучения. Если они не задуманы как совместимые, нет никаких оснований считать, что две безопасно сконструированные системы ИИ, разработанные разными компаниями для разных целей, спонтанно объединятся и направят усилия на некую общую великую цель без человеческого вмешательства. Конечно, глобализация означает, что у современных гигантских компаний есть большое стремление приводить вещи в гармонию друг с другом, чтобы завладеть рынком и получать больше прибыли...

Но могут ли системы ИИ и тела роботов, в которых они установлены, пройти тест и завладеть миром? Предположительно, только если мы, умные, но слабые людишки, разрешим им и серьезно поможем. Но зачем нам это делать? Может быть, из-за нашей человеческой глупости?

Глава 9
Сетки, графика и игры

Сетки и игры имеют важное значение. Сетки являются основой для многих игр. Кроме того, они занимают особое место в информационных технологиях. Например, они позволяют показать изображения. А игра о жизни, основанная на решетке, открыла абсолютно новое направление в информатике. Правила другой компьютерной игры на основе решетки помогут объяснить, почему люди больше не являются лучшими игроками на планете. Программисты превратили саму жизнь в одну из таких игр.

Решетки и игры как изображения

Игры как высокотехнологичная область искусства

История компьютерных игр довольно коротка, но отрасль настолько разрослась, что сегодня стоит дороже, чем киноиндустрия. Играете ли вы за тролля в Warcraft или деретесь с назойливыми свинками в Angry Birds, за этим стоят компьютерные программы, установленные в игровых приставках, ноутбуках, смартфонах и планшетах, которые мы носим с собой по всему миру. Они обеспечивают нам и развлечения, и новые способы взаимодействия с другими людьми.

Полные видеоигры можно разделить на две основные категории. Над большими играми работают многие сотни людей — программисты, дизайнеры и художники. Они используют и науку — например, в физических движках, компьютерных программах, которые моделируют физические законы виртуального мира. Эти движки определяют, как падают камни или как ткань развевается на ветру. Конечно же, здесь мы наблюдаем пример компьютерного моделирования, только оно используется скорее для развлечения, чем для исследований. Сегодня видеоигры представляют собой сплав информатики и художественного творчества. Как сказал пионер отрасли Ричард Гэриотт, это квинтэссенция высокотехнологичного искусства.

Вторая основная категория игр — независимые игры, в основном разрабатываются для смартфонов. Здесь для результата хватит небольшой группы увлеченных и творческих программистов и дизайнеров. Появление рынка приложений для смартфонов привело к взрывному росту новых идей и тем, которые можно исследовать и развить. Это особенно верно для игр, интегрированных в социальные сети (наши так называемые социальные графы), в которых все мы проводим много времени. Говорят, идея для приложения найдется у каждого, и с небольшой помощью вы сможете сами что-нибудь создать. Если вам интересно, можно взять бесплатный программный пакет из интернета, который позволит превратить ваши идеи в код для смартфона. Потом его можно скачать на свой телефон и удивить друзей.

Пиксельные картинки

В основе своей компьютерные игры строятся на компьютерной графике и изображениях (хотя можно ждать появления компьютерных игр, в которые вы будете играть в реальном мире и при этом задействовать все органы чувств!). Изображения, которые мы видим на экране, состоят из многих тысяч пикселов. Пикселы — это просто элементы картинки, маленькие точки на экране. Их яркость и цвет можно изменять, потому что они представлены в виде цифр. Если экран достаточно велик, можно создать абсолютно любое изображение, установив для пикселов определенное значение с помощью правильно подобранных чисел. Чем больше пикселов, тем выше разрешение и тем более детальное и четкое изображение мы можем получить. На рис. 54a изображена голова робота из 64 пикселов (8×8). Рисунок едва узнаваем, поскольку пикселов не хватает, чтобы показать детали. На рис. 54b — та же картинка, но пикселов уже 256 (16×16). Очевидно, что это голова робота. Если добавить еще пикселов, то есть увеличить разрешение, картинка может стать еще более подробной — например, на ней можно показать форму глаз, носа и рта.

Сам экран компьютера можно считать решеткой, и в таком случае игра — это серия изображений, которые мы контролируем (снова представление в действии).

Изображения можно создавать самыми разными способами с помощью компьютерной графики. Простые растровые методы подразумевают сохранение каждого пиксела. Нашу первую картинку можно сохранить в виде 64 цифр:

Здесь 0 означает белый пиксел, а 1 — черный пиксел. Мы создаем изображения, продвигаясь по линиям сверху вниз и быстро устанавливая значение пикселов.

Чем больше пикселов, тем яснее изображение, но и тем больше цифр необходимо сохранить, чтобы представить его. Чтобы сохранить изображение робота в более высоком разрешении, нам понадобится 256 цифр вместо всего лишь 64:

Для этих изображений мы выбираем одну из всего двух цифр на каждый пиксел — 1 или 0, поэтому у нас всего два цвета, белый и черный. Если использовать больше цифр, где каждая будет представлять свой цвет, то можно подобным образом сохранять цветные изображения.

Альтернативное представление изображения — сохранить его в виде линий и фигур, из которых оно состоит. Это так называемые векторные методы. Мы определяем начальные и конечные точки для тысяч линий и быстро рисуем их на экране. Например, чтобы нарисовать квадрат, вместо обозначения каждого пиксела в сетке вы сохраняете серию инструкций:

Линия (Север, 50)

Линия (Восток, 50)

Линия (Юг, 50)

Линия (Запад, 50)

Чтобы нарисовать изображение, мы просто выполняем инструкции. Такое представление в целом занимает гораздо меньше места, но у него есть еще одно большое преимущество. Инструкция выше позволяет нарисовать квадрат со стороной 50. Допустим, мы хотим получить изображение в 10 раз больше. В этом случае просто умножаем все значения на 10. Если же мы хотим, чтобы квадрат был в 10 раз меньше, то делим их на 10. Благодаря этому представлению мы можем увеличить изображение до любого размера, например чтобы показать его на большом экране, но без необходимости хранить еще больше данных и не теряя точности.

Вот почему представление диаграмм как в pdf-файлах занимает меньше места и выглядит одинаково хорошо, как бы вы ни увеличивали изображение. В таких файлах хранятся векторные версии. Изображение в формате jpeg требует больше памяти, чтобы сохранить картинку в более высоком разрешении, и при сохранении нужно указать, каким именно оно будет. Вот почему, приближая изображение в формате jpeg, вы видите, что все расплывается и линии становятся неровными.

С помощью векторных методов мы создаем трехмерные формы, объединяя много, порой десятки тысяч, так называемых графических примитивов — сфер, кубов, цилиндров и так далее. Различные комбинации позволяют нам создавать желаемые сложные формы.

Существуют системы, которые симулируют распределение световых лучей в искусственном мире (для этого требуется компьютерное моделирование — на сей раз чтобы показать, как источники света освещают предметы). С их помощью создают фотореалистичные изображения. Кроме того, к нашим графическим примитивам добавляют скрипты, отвечающие за сложные движения персонажей, — их часто создают, снимая движения настоящих актеров, — и таким образом фигуры будут двигаться как мы хотим. Ограничения — это объем доступных вычислительных мощностей, качество кода, который пишут кодировщики-программисты, чтобы графика выглядела еще естественнее, и воображение творческого человеческого ра­зума. Но даже простая сетка и несложные правила кодирования могут дать замечательные результаты.

Жизнь как игра

Играем в сетке

Давайте начнем с простого — с игры, в которой есть квадратная сетка и набор правил, в зависимости от которых на ней появляются и исчезают пикселы. Значение пиксела меняется и зависит от того, сколько других пикселов находится рядом. Звучит не очень интересно, правда? Но не торопитесь с выводами. Даже в этой простой игре происходит много интересного, и мы используем ее, чтобы кое-что понять о мире природы.

Игра называется «Жизнь», ее автор — математик Джон Конвей. Впервые правила игры были опубликованы в 1970 г., и впоследствии она приобрела популярность у программистов по всему миру. Правила просты, хотя Конвей приложил массу усилий, чтобы их правильно сбалансировать и гарантировать интересный игровой процесс.

Сетка представляет собой небольшой квадратный мир с клетками (пикселами), которые могут присутствовать (быть живыми) и отсутствовать (быть мертвыми). У каждой клетки есть окружение из восьми других, которые непосредственно прилегают к ней по горизонтали, вертикали и диагонали. Чтобы выжить, существующая живая клетка должна иметь два или три живых соседа — этого достаточно для поддержания жизни, но не слишком много. Если у любой живой клетки окажется менее двух соседних, она умрет из-за недостаточной населенности. Подобным образом любая живая клетка, у которой более трех живых соседей, умрет от перенаселения. Наконец, каждая живая клетка, у которой есть три живых соседа, активизируется и имитирует процесс размножения. Эти принципы обобщены в порождающих правилах на рис. 55.

На рис. 56 показан пример такой модели и один жизненный цикл.

Благодаря этой простой математике и простому набору порождающих правил, которые применяются к клеткам на сетке, на игровом поле возникают странные и интересные модели, которые с течением времени меняются. Клетки живут и умирают по заданным правилам.

Сыграйте сами

Вы можете сыграть в эту игру самостоятельно. Для этого понадобится большая сетка. Для начала сгодится шахматная доска, но вы скоро осознаете, что нужно больше пространства. Больше подойдет доска для игры в го, если она у вас найдется. Как вариант, можно нарисовать большую сетку на самом большом листе бумаги, какой вы только найдете. В идеале лист должен быть бесконечным, но тогда он не поместится в вашу спальню… поэтому придется принять, что, если игра дойдет до края доски, нужно будет быстро найти еще место либо признать, что это конец «Жизни» и все ваши существа упадут с края «вселенной».

Необходимо как-то помечать рождающиеся клетки. Полезно также выделять те, которые в следующем раунде умрут. Убирать их нельзя — они нужны, чтобы просчитать все изменения. К примеру, можно взять камни для игры в го — замените черные на белые, чтобы показать, какие клетки скоро умрут (и отправятся на небо). Еще вам понадобится как-то помечать квадраты, в которых зародится жизнь. Для этого используйте более мелкие предметы (например, бусины) другого цвета. Можно использовать три вида монет или цветных бусин (но, если в вашем мире закипит жизнь, их понадобится очень много).

Теперь остается только произвольно разместить фишки на доске, а потом рабски следовать законам «Жизни». В вашем мире это эквиваленты физических законов. Сначала определите все рождения и смерти, заменив фишки на новые на всей доске, а потом уберите умирающие клетки и замените живые на новорожденные, чтобы подготовиться к следующему раунду. Чтобы играть в «Жизнь», нужно уделять много внимания деталям. Если вы сделаете ошибку с одной клеткой, у вас получится совершенно другой расклад.

В интернете вы найдете самые разные симуляции и с их помощью увидите, как развивается жизнь в более крупных масштабах. Конечно, если вы умеете программировать, то попробуйте создать собственный вариант. В систему Turtle («Черепаха»), разработанную в Оксфордском университете (www.turtle.ox.ac.uk), входит программа игры «Жизнь», которая может послужить образцом.

Паноптикум жизни

Конвей обнаружил, что некоторые комбинации являются статичными. Они остаются в одном и том же месте игрового поля без изменений, поэтому он назвал их натюрмортами — как, например, змею на рис. 57. Какие еще простые начальные комбинации, относящиеся к натюрмортам, вам удастся найти?

Некоторые шаблоны меняют форму, проходя через фиксированный набор вторичных шаблонов, в конце концов возвращаются к исходному варианту — и снова начинают бесконечный повторяющийся цикл. Их назвали осцилляторами. Например, очень простой осциллятор, так называемая мигалка, показан на рис. 58. Если начать с набора мигалок, которые находятся на достаточном расстоянии, чтобы не мешать друг другу, вы создадите замечательные мерцающие узоры. Такие комбинации из группы осцилляторов называются пульсарами — по имени необычных звезд, на которых с определенной периодичностью происходят всплески энергии.

Коллега Конвея Ричард Гай натолкнулся на удивительные фигуры, которые сохраняют форму, но передвигаются по сетке. Их назвали планерами (рис. 59). В целом движущиеся конфигурации называют космическими кораблями.

В игре «Жизнь» даже можно имитировать логические вентили. Как мы говорили выше, это базовые составляющие компьютера. Их делают из транзисторов, нейронов и… из клеток игры «Жизнь». Это значит, что, располагая достаточно большой сеткой, можно создать на ней работающий компьютер — исключительно из клеток, следующих этим простым правилам.

Моделируем новые миры

Информатики начали предлагать новые разновидности игры — трехмерные решетки, шестиугольную решетку и так далее. Изменив игровое пространство и правила, они обнаружили, что по мере того, как компьютер повторяет нужные действия и вносит изменения, на решетке появляются еще более интересные конфигурации.

Со временем изобретение Конвея стали называть клеточным автоматом и сочли новым способом проводить вычисления. Правила можно адаптировать так, чтобы клетки проводили вычисления разного рода. Простые клетки с простыми правилами можно заменить и даже усложнить. Каждая клетка в этом случае становится автоматом, который находится в определенной позиции на решетке и содержит код с собственным набором правил. Когда автомат входит в контакт с информацией, размещенной на решетке, он «переваривает» сначала свои данные, а затем данные из ближайших окрестностей, и на выходе дает результат. Результат зависит от нескольких предыдущих (скажем, 10) состояний клетки. Изначальными правилами Конвея при этом полностью пренебрегают.

Такого рода сложные клеточные автоматы находят самое разное применения. Их, например, настраивают на изучение природы — чтобы они исследовали, как в тропических лесах распространяются растения, как развиваются коралловые рифы, как проявляется сейсмическая активность, как мигрируют животные. Каждая клетка при этом становится абстракцией небольшого участка мира. В ней закодированы правила поведения и взаимодействия с другими клетками, свойственные интересующему ученых объекту. Клеточные автоматы обеспечили новый способ изучения экологии с помощью компьютерного моделирования на основе клеток.

Клеточный автомат помогает понять, как на дорогах образуются пробки и как в популяции распространяется болезнь. В криптографии данные, которые нужно зашифровать, размещают в сетке и исследуют с помощью автомата. Благодаря простым правилам каждый в состоянии зашифровать сообщение. Но расшифровать его, не зная ключа, нелегко. Клеточные автоматы даже использовали для сочинения музыки — и для многих других задач. Неплохой результат для того, что началось с несложной игры на простой доске.

Игры, в которые играют люди

Любите играть в слова?

В игре Конвея не было двух конкурирующих игроков, то есть отсутствовал соревновательный момент, который часто привлекает нас в играх. Вот простая игра под названием «Бусы, хлеб, хлеб», в которую мы сейчас попробуем сыграть (возможно, вас порадует, что в баню идти не придется). Сначала рассмотрим правила. Запишите слова:

БУСЫ, ХЛЕБ, БАНЯ, ПЛУГ, СНЕГ, ГАТЬ, УРОН, ОРЕХ, МАРС.

Вот правила:

1. Первый игрок выбирает слово из списка, вычеркивает его из списка и записывает.

2. Второй игрок делает то же самое с еще не вычеркнутым словом.

3. Игроки продолжают ходить до тех пор, пока кто-нибудь не выиграет. Победителем становится тот, кто первый сможет собрать три слова с одной и той же буквой.

Например, игра может пойти так:

игрок 1 берет БУСЫ,

игрок 2 берет ХЛЕБ,

игрок 1 берет БАНЯ,

игрок 2 берет ГАТЬ,

игрок 1 берет ПЛУГ,

игрок 2 берет ОРЕХ,

игрок 1 берет УРОН...

…и выигрывает, собрав БУСЫ, ПЛУГ и УРОН. Это три слова, в которых есть буква У.

Сыграйте несколько партий, чтобы понять принцип. А потом читайте дальше — и найдете хитрый способ выигрывать… а может, догадаетесь сами? Мы вернемся к этому чуть позже.

ПОДСКАЗКА. Подумайте, как расположить слова в квадрате, чтобы было легче заметить выигрышный набор слов. Вы уже знаете очень похожую игру!

Как обыграть человека

Мы знаем, что компьютеры творят чудеса, и одно из таких чудес — умение выигрывать у людей в игры. Компьютер может победить чемпиона мира по шахматам, но как? А может ли обычный листок бумаги действовать столь разумно, что будет играть так же хорошо, как человек? Да. Если правила будут верными. И сейчас у вас есть шанс сыграть против такого листка и посмотреть, что получится.

Крестики-нолики — популярная игра на основе сетки, позволяющая быстро развлечься и посоревноваться. Давайте сыграем — и заодно рассмотрим базовые принципы, благодаря которым компьютеры могут участвовать в играх. В игре «Крестики-нолики» участники по очереди делают ход на поле 3×3. Один ставит нолики, другой — крестики. Сделать ход — значит написать X или 0 в пустой клетке на доске. Первый, кто поставит три символа в одну линию по горизонтали, вертикали или диагонали, выигрывает. Если никому не удастся это сделать, получается ничья.

Игра со страницей, на которой напечатан рис. 60, будет нелегкой! Когда настанет ее очередь ходить, делайте, что сказано в инструкциях к рисунку. Потом делайте любой ход. Страница начинает первой и играет крестиками.

Ну что, выиграла страница? Или получилась ничья? Или вам все же удалось обыграть этот листок бумаги?

В лучшем случае (если вы не мухлевали) будет ничья. Удалось ли странице сыграть достойную партию? Она немного разбирается в крестиках-ноликах и действует осмысленно. Как и в игре «Жизнь», для выигрыша здесь тоже требуются тщательно продуманные и проверенные инструкции — знакомый нам теперь алгоритм. Обычно такие инструкции хранятся в памяти компьютера, чтобы он им следовал.

Но компьютеры делают только то, что придумал программист. Если что-то пойдет не так, его действия окажутся не слишком разумны. Мы написали правила, приведенные выше, в расчете на то, что страница будет ходить первой… а если она начнет второй? Попробуете? Так ли умно она играет? Мастерство программиста заключается в том, чтобы написать правила для любой вероятности. Хотите написать хорошие инструкции для игрока 2? Позаимствуйте знания у нашего листка бумаги, и вы будете непобедимы.

Но действительно ли это интеллект? Ведь тут просто выполняются кем-то написанные правила. Может быть, надо обращать внимание на результат. Лист бумаги и правда играет так же хорошо, как лучшие игроки-люди, и он непобедим — по крайней мере когда ходит первым. В более сложных играх, например в шахматах, алгоритмы должны быть более изощренными, но идея остается прежней. Для этого алгоритма человек разработал точную последовательность ходов. Однако шахматы слишком сложны, чтобы заранее определить все необходимые для победы правила. Поэтому компьютерам-шахматистам необходим алгоритм, указывающий, как прийти к победе самостоятельно.

Сегодня компьютеры обыгрывают в шахматы гроссмейстеров. Раньше мы считали, что шахматы — самый сложный тест для компьютерного интеллекта. Однако если у вас есть быстрая и достаточно изощренная программа плюс достаточный объем памяти, чтобы компьютер мог просчитать тысячи и тысячи возможных комбинаций для любой позиции на доске, то следует выбрать ту, которая открывает возможности для наилучших позиций — и таким образом позволяет обыграть человека. Это называется поиском по дереву. Мы использовали подобный алгоритм при разработке инструкции для безупречной партии в крестики-нолики. Однако в шахматах слишком много вариантов, чтобы подобным образом охватить все. Шахматные компьютеры смотрят на много ходов вперед, но не до конца игры. Хороший шахматист-человек не просто просчитывает абсолютно все ходы — он ищет знакомые комбинации и формирует определенную последовательность. Он играет путем сопоставления с образцом.

Существуют и более сложные настольные игры, которые ставят перед компьютерами новые задачи, — например, древняя игра го. В отличие от шахмат, го — популярная стратегическая игра для двоих, у которой простые правила и в которую играют на поле-сетке 19 на 19. Однако число возможных сочетаний на доске огромно, и, чтобы провести такой анализ, о котором мы говорили выше, нужно просчитать число ситуаций, превышающее число атомов во вселенной. Компьютеры не могут выиграть в го, как выигрывают в шахматы.

Поэтому исследователи подошли к го иначе, чем к шахматам, для которых компьютер запрограммировали именно на хорошую игру. Чтобы победить мастера го, компьютерную программу AlphaGo снабдили мощным обучающим алгоритмом общего назначения, в котором использовали уже рассмотренные нами методы. Алгоритм AlphaGo извлекал победные комбинации из сыгранных партий и совершенствовал навыки с каждым выигрышем или поражением. В итоге в 2015 г., многому научившись, AlphaGo выиграла у профессионального игрока в го в турнире из нескольких партий. В 2016 г. она победила одного из лучших мастеров мира Ли Седоля в турнире из пяти партий со счетом 4 : 1. Это еще один успех на счету искусственного интеллекта, который играет в игры.

Компьютер играет и в другие типы игр без доски, например в покер. Предназначенные для этой игры покерные боты могут выиграть у человека, но им приходится иметь дело с иным типом игровой сложности. В отличие от шахмат и го, где все на виду, покер — игра с неполной информацией. Вам неизвестно, какие карты есть у других игроков и какие карты сдадут. Покерные боты часто обращаются к вероятности, чтобы сделать наиболее верную догадку, — почти как искусные игроки. Исследования в этой области помогают ученым понять, как мы, люди, справляемся с риском и принимаем решения.

Совершенствуем игру

Четко описанные наборы правил для ИИ вроде нашего алгоритма для крестиков-ноликов постоянно возникают в настоящих играх. Часто они стоят за компьютерными версиями настольных игр, в которые играют против компьютера. В многопользовательских играх бывают так называемые «несобственные персонажи» (за которыми не стоят игроки). В них интегрированы правила для искусственного интеллекта, контролирующие их взаимодействие с настоящими игроками, что делает игровой процесс интересным и достоверным. Также ИИ часто следит за показателями игроков-людей, чтобы игра была достаточно сложной и интересной. В зависимости от этого, например, выбирается уровень сложности. Иногда искусственный интеллект скрыт и решает другие задачи — например, выясняет, на какой телефон и экран какого размера загружается приложение, или проверяет, достаточно ли хорошо работает сетевое соединение. Еще он фиксирует, насколько хорошо справляются игроки, какие роли они выбирают чаще всего и реже всего, по каким причинам они прекращают игру и что оказывается слишком трудным для большинства игроков. Все эти данные позволяют разработчикам адаптировать игровой процесс к потребностям и повысить объем покупок в игре.

Как выиграть в «Бусы, хлеб, баню»

Давайте вернемся к нашей игре. Проследить, какие слова выиг­рают, довольно сложно, если не знать один трюк. Разместите слова в квадрате, как показано на рис. 61 (проследите, чтобы противник этого не увидел). Вычеркивайте слова по ходу игры, используя X для своих ходов и O — для ходов другого игрока.

Сыграйте несколько партий. Теперь гораздо легче решить, куда двигаться. Если у вас три слова на одной линии, то окажется, что есть и три одинаковые буквы. Если у противника любые два слова в одной линии, то нельзя допустить, чтобы он поставил туда третье. Теперь вы просто играете в крестики-нолики, а ваш противник режется в «Бусы, хлеб, баню». Это абсолютно одинаковые игры — на победу работает один и тот же принцип!

Расположение слов в квадрате играет важную роль. Слова с одной и той же буквой стоят в одну линию. Это значит, что, выбирая три слова с одной буквой, вы ищете линии (визуальный образец), а не читаете слова. Если вы отлично умеете играть в крестики-нолики (используя инструкции, то есть алгоритм, приведенный выше), то в игре «Бусы, хлеб, баня» вам тоже не будет равных. Один алгоритм выигрывает в обеих играх.

Итак, мы провернули трюк с вычислительным мышлением, который использовали в головоломке с экскурсоводом. Мы определили, что, если изменить представление, задача окажется такой же, как уже решенная. В этом случае берут решение из предыдущей задачи и применяют его к новой. Задачи обобщают до одного уровня, а значит, и решения тоже.

Как мы видим

Почему игра становится легче, когда слова вписаны в сетку, а не показаны списком? Разница исключительно в том, что информация теперь представлена так, что мозгу легче ее обрабатывать. Наш мозг отлично выделяет визуальные закономерности — для этого требуются совсем небольшие усилия (мы вернемся к этому в следующей главе). Это гораздо проще, чем искать буквы и запоминать слова в списке. Способ структурирования и представления информации играет большую роль. Это еще один пример, который показывает, почему выбор подходящего представления данных так важен. Он упрощает сложную задачу.

Это одна из причин, по которой графические интерфейсы пользователей — усовершенствование по сравнению со старыми системами, которые требовали ввода команд. Благодаря графическому интерфейсу вы обрабатываете информацию визуально, не прибегая к словам. Сопоставление с образцом при поиске необходимого — это зрительное сопоставление, не связанное с обработкой и пониманием слов.

В наши дни игры необходимо разрабатывать с учетом ощущений пользователя. Например, приложения должны привлекать ваше внимание и быть понятными сразу, в противном случае их удалят. Дизайнеру необходимо знать, как работает мозг, и обязательно учитывать это — таким образом можно гарантировать, что пользователю легко вступить в игру и что игровой процесс интуитивно понятен.

Игры, игры повсюду

«Жизнь» Конвея — это игра, но настоящая жизнь сегодня тоже превращается в игру. Философия игр и их популярность находят новое применение благодаря идее геймификации. В ходе этого процесса элементы и принципы игры используются в новых нетипичных сферах, например чтобы людям было увлекательнее учиться, заниматься спортом, производительно работать в офисе. Элементы игры даже применяют для борьбы с пассивностью избирателей.

Эти приемы эксплуатируют естественную склонность многих к конкуренции, совершенствованию навыков, стремлению к достижениям или повышению статуса в группе друзей. В играх могут участвовать «игроки», работающие вместе или соревнующиеся друг с другом. Они зарабатывают награды в виде баллов, знаков отличия, виртуальной валюты или перехода на новый уровень. Награды видимы для всех, например в таблице лидеров, что поощряет игроков выполнять задания. Однако этот выраженный соревновательный элемент нравится не всем, поэтому многие приложения в плане геймификации рассчитаны на то, чтобы человеку было интересно заниматься предложенным и чтобы это было похоже на игру.

Также существуют игры, которые не просто доставляют удовольствие игрокам, но и помогают решить важные научные и культурные задачи. Например, сегодня одни игры помогают сортировать огромные объемы данных о форме галактик, разрабатывать лекарства или каталогизировать древние рукописи. Другие помогают тегировать изображения в сети хорошими описаниями, чтобы облегчить слабовидящим восприятие изображений. Таким образом коллективные интеллектуальные ресурсы и навыки людей-игроков помогают компьютеру сортировать для обработки сложные данные. Человеческий мозг все еще справляется с этим лучше.

Компьютеры уже могут победить лучших игроков-людей в шахматы и го, однако еще есть игры, в которых люди сильнее. Обычно в них играют на сетке, и они ближе к настоящей жизни.

Глава 10
Видим за деревьями лес

Сопоставление с образцом — основа вычислительного мышления; образцы можно найти повсюду. Программистам необходимо разбираться в образцах и уметь создавать алгоритмы, работающие с образцами. Чтобы понять, как развивается этот процесс, рассмотрим поиск образцов в алгоритмах, лежащих в основе трюка с чтением мыслей. Используя обобщение в виде математических теорем, мы придумываем и такого рода фокусы, и другие безошибочно работающие алгоритмы. Те же идеи стоят за мощными алгоритмами, которые позволяют компьютерам видеть мир так же, как его видят люди. Создавая алгоритмы, которые могут как найти, так и использовать образцы, мы пишем еще более полезные программы. Мы учим компьютеры вычислительному мышлению, чтобы они могли делать то, что делает человек, и не хуже него.

Магия чтения мыслей

Образцы повсюду

Сколько раз вы смотрели на облака в летний день и видели пушистых животных или узнавали лицо кинозвезды в расползшейся на тарелке глазунье? Это наш мозг ищет образцы в окружающем мире. Приведенные примеры показывают, что обнаруженные образцы возникают случайно. Но порой важна способность увидеть их сознательно. От этого иногда зависит наша жизнь.

Находить и предсказывать образцы, пожалуй, главная задача нашего мозга. Он старается обнаружить их в поле зрения, чтобы мы видели предметы, или в звуках, чтобы мы слышали слова. Другие шаблоны связаны с планированием решений и наших действий. Эти решения основаны на знаниях образцов, полученных благодаря прошлому опыту. Кроме того, нам нравятся образцы. С ними мы чувствуем себя комфортно. Например, телевизионные новости подаются по шаблону: нам сообщают, что покажут дальше, потом показывают сюжет и, наконец, напоминают, что показали... Эти три стадии делают просмотр удобным.

Литература полна повторяющихся образцов, которые мы знаем и используем. Мономиф — идея писателя и исследователя мифологии Джозефа Кэмпбелла, высказанная в 1949 г. В соответствии с ней герой следует знакомой модели, которая повторяется в фильмах и книгах, старых и современных. Он отправляется навстречу приключением, сталкивается со сложным вызовом, преодолевает его и возвращается домой другим человеком. Этот образец, имеющий эффектную трехчастную структуру (начало, середина и развязка), постоянно повторяется в литературе — в «Одиссее» Гомера, во многих пьесах Шекспира и во «Властелине колец» Толкина. Кроме того, он лежит в основе таких фильмов, как «Звездные войны» и «Индиана Джонс». Представляется, что образец структурирует эти истории, и поэтому нам интересно и легко за ними следить — а в конце мы испытываем чувство удовлетворения.

Мы уже видели, что сопоставление с образцом лежит в основе вычислительного мышления. Оно необходимо и для выявления абстракций и обобщений, для составления порождающих правил и для выбора удачного представления информации. Специалисты по компьютерным наукам тоже хотели бы найти оптимальные способы выявлять и предсказывать образцы. Они используют вычислительное мышление, чтобы самые удачные способы для сопоставления с образцом как таковым и результаты этого принимали форму сложных алгоритмов, которые используются в компьютерах, позволяя им проводить сопоставление с образцом самостоятельно. Таким образом вычислительное мышление применяется к идеям, стоящим за вычислительным мышлением.

Например, алгоритмы для сопоставления с образцом применяют, чтобы рассматривать, например, химические основания в составе нашей ДНК и искать в них шаблоны, соответствующие особым типам заболеваний. Также с их помощью пытаются предсказать флуктуации на финансовых рынках, чтобы найти ключ к конкурентному превосходству. Порой они предсказывают, как виртуальные персонажи в компьютерных играх должны реагировать на образцы, выявленные в вашем игровом стиле, чтобы поддерживать в вас интерес. Порой они даже помогают машинам «увидеть» мир так, как его видим мы. Почему бы машинам тоже не видеть животных в облаках? Образцы есть повсюду — вопрос только в том, чтобы их найти.

Волшебные слова — коды и колдовство

Давайте посмотрим на простые алгоритмы сопоставления с образцом, чтобы понять, о чем идет речь. Фокусники давно поняли: если им известна простая закономерность, о которой вы не догадываетесь, это можно использовать для создания волшебных эффектов. Например, практика телепатии имеет долгую и славную историю. Находящемуся на сцене фокуснику завязывают глаза, а его помощник собирает какие-то предметы у зрителей. Затем благодаря «ментальной связи» человек с завязанными глазами описывает собранные предметы, не видя их. Для этого используются специальные вербальные коды, и, чтобы освоить этот фокус, артистам приходится много запоминать.

Например, если выбранный предмет — ручка, ассистент, допустим, говорит: «Итак, что у меня в руке?» Если это карманные часы, ассистент задает вопрос иначе: «Какой предмет у меня в руке? Хорошо подумай. Время есть». Конечно, все это довольно грубые примеры — фокусники действуют гораздо тоньше, и поэтому их правила труднее запомнить. Такие выступления были очень популярны в прошлом, и артисты разрабатывали все более и более изощренные словесные коды. Закономерность была спрятана у всех на виду в произносимых словах, и расшифровка кода позволяла осуществить невозможное на сцене.

Учитесь читать мысли

Вы можете поэкспериментировать со скрытыми закономерностями и попробовать себя в чтении мыслей. Для рассматриваемого варианта не нужна столь же хорошая память, как для традиционного. Вам потребуется сообщник — партнер, который в курсе дела, и зрители. Во время выступления (постарайтесь, чтобы ваши действия выглядели загадочными и таинственными) человек из вашей команды, фокусник, выходит из комнаты. Затем зрители втайне от него выбирают предмет, который маг должен назвать по возвращении.

Ассистент остается в комнате, где делают выбор, чтобы «гарантировать честную игру и проследить, чтобы никто не передумал». После возвращения мага ассистент начинает ходить по комнате — вроде бы безо всякой цели — и указывает на разные предметы, каждый раз задавая один и тот же вопрос: «Это выбранный предмет?» И каждый раз маг отвечает правильно.

Вместо того чтобы запоминать сложную последовательность словесных кодов, можно с тем же эффектом использовать простое сопоставление с образцом на основе прогнозирующего алгоритма. Заранее условьтесь с ассистентом о каком-то предмете — например, лампе. Что бы вы ни выбрали, назовем это x. Секретный сигнал состоит в том, что, когда ассистент указывает на этот объект, вы понимаете, что следующий (назовем его y) и будет избранным. Ваш общий секрет — алгоритм, приведенный на рис. 62. Конечно, нужно заранее договориться, что вы обозначите, как x.

Если вас попросят снова показать фокус и попытаться угадать серию предметов, закономерность станет слишком очевидной. С этим легко справиться, применив немного алгоритмического мышления и расширив алгоритм. Каждый раз, выполняя фокус, вы используете разные предметы, прежде чем указать на выбранный, — например, лампу, потом ковер, потом выключатель. Теперь x меняется каждый раз. Код для совместного использования может выглядеть примерно как на рис. 63.

Конечно же, перед началом вам надо убедиться, что у вас есть лампа, ковер и выключатель. Вы указываете на лампу, пытаясь угадать первый предмет (когда номер попытки — 1), ковер при угадывании второго предмета (когда номер попытки — 2) и выключатель для третьего раза (когда номер попытки — 3). Последнее утверждение по умолчанию — на случай, если вас попросят найти четвертый, пятый или даже шестой предмет. Некоторых людей невозможно удовлетворить! К этому вы не готовы, но правильное алгоритмическое мышление должно обеспечить варианты на любой случай. Поэтому у вас есть отговорка по умолчанию, если кто-то из зрителей будет настаивать на продолжении после трех заготовленных чудес ясновидения: «Мои экстрасенсорные возможности истощены. Прошу прощения, я не могу продолжать».

Если образец подводит, что тогда получится?

Этот алгоритм сопоставления с образцом в большинстве случаев позволит вам развлечь аудиторию, но иногда возникают проблемы. Логика наших рассуждений должна быть безупречной в каждой детали. Возможно, вы подумаете, что охватили все варианты, но если вторым предметом, выбранным аудиторией, окажется красивый ковер, который вы хотели использовать как второй сигнал? В алгоритме сопоставления с образцом появляется проблема. Незапланированная в нашем алгоритме неожиданность. Получается, надо показать на ковер — а потом снова показать на ковер! Это будет выглядеть не слишком-то волшебно.

Конечно, во время фокуса вы как человек будете импровизировать на ходу и выкручиваться с помощью юмора — например, действительно два раза покажете на ковер и пошутите на эту тему. Но если вы запрограммировали робота-фокусника, который точно следует алгоритму, то все будет выглядеть глупо. Робот сможет пошутить только в том случае, если вы предусмотрели возможные проблемы и добавили в алгоритм код для соответствующих шуток.

Итак, если робот-фокусник не справится с задачей, это не конец света. Но если бы речь шла об алгоритме сопоставления с образцом, который определяет, выполнены ли в правильном порядке все разнообразные действия, необходимые для выпуска посадочных шасси воздушного судна, и в нем возникла бы похожая проблема, случай был бы совсем другим. Продумать все вероятные ситуации и предусмотреть для них встроенное сопоставление с образцом сложнее, чем представляется, но программистам это необходимо, чтобы их программное обеспечение работало правильно.

В так называемых системах с особыми требованиями к безопасности эксплуатации есть целый ряд образцов, которые обязательно нужно найти и на которые нужно правильно отреагировать, — например, в ПО для больниц, для управления ядерными реакторами или самоуправляемых машин нового поколения. Если мы просто учтем массу возможных вариантов, то все равно нам не удастся охватить все. Поэтому в информатике используются логическое и аналитическое мышление и создаются математические способы анализа таких систем — например, они могут базироваться на идеях, которые мы применили к решению головоломок в главе 4. Математика обеспечивает нам более мощный инструмент для поиска образцов в системе. Потом пишутся программы, реализующие логическое мышление, основанное на математике. Компьютеры гораздо лучше нас изучают возможности и ничего при этом не упускают. Компьютеры в огромных объемах занимаются за нас вычислительным мышлением.

Простая магия

Простые числа в математических фокусах

Давайте рассмотрим другой тип фокусов, основанных на сопоставлении с образцом, — тип, который работает всегда (всегда, всегда, всегда), потому что нам известны математические принципы, стоящие за его закономерностями. В математике как таковой крайне важна способность видеть и понимать закономерности, а потом превращать их в общие факты, которые называют теоремами, — здесь мы снова наблюдаем метод обобщения, относящийся к вычислительному мышлению (основы вычислительного мышления были почерпнуты в самых разных источниках). Математика хорошо сочетается с магией, и, как только математики и программисты находят закономерности, фокусники могут использовать их в магических трюках.

Предложите трем друзьям ввести произвольное число в калькуляторы (или мобильные телефоны, если в них есть калькулятор). Скажите, что вы в точности предскажете, на какие числа будет делиться выбранное произвольное число. В калькуляторе можно указать абсолютно любое трехзначное число. Это их выбор. Однако этот выбор нужно держать в тайне от вас.

Притворитесь, что угадываете их мысли, и скажите, что три цифры — это слишком просто. Чтобы усложнить задачу, нужно увеличить числа. Чтобы им было проще, а вам — сложнее, они должны еще раз ввести то же самое трехзначное число, и тогда у каждого получится шестизначное. Например, если изначально они ввели 345, их новым числом будет 345 345.

Вы напрягаете свои телепатические возможности и сразу же называете разные маленькие числа, на которые их личные шестизначные числа делятся без остатка. Вы ответственно заявляете, что, хотя совершенно не представляете, что за числа они ввели, у первого друга число точно делится на 7, у второго — на 11, а у третьего — на 13. Остатка не будет. Друзья выполняют деление на калькуляторе, проверяют результат и показывают, что вы правы. Как вы и предсказали, остатка нет.

В заключительной части фокуса вы говорите, что моментально вычислите шестизначное число, которое будет без остатка делиться на три маленьких числа, которые вы уже дали, — три «случайных» числа, полученных из других, которые в начале выбрали ваши друзья. Вы называете шестизначное число, и снова калькулятор показывает, что вычисления в уме оказались абсолютно верными.

Магические совпадения совершенно случайны?

Секрет в том, что три названных вами маленьких числа — это всегда 7, 11 и 13. В остальном фокус является алгоритмическим и работает сам — он основан на математическом факте. Если записать число из трех цифр и дописать к нему те же самые три цифры, то у нас получится тот же результат, что и при умножении этого трехзначного числа на 1001. Почему? Умножая число на 1000, нужно поставить в конце три ноля. Умножая на 1001, мы умножаем на 1000 и приписываем в конце изначальное трехзначное число вместо трех нолей.

Например, 345 345 — это 345 × 1001 (345 000 + 345). Маленькие числа, которые вы используете в предсказании, — 7, 11 и 13. Однако 7 × 11 × 13 = 1001. Это значит, что, когда вы таким образом дублируете число, например 345, вы умножаете его на эти три числа. То есть 345 345 = 345 × 1001 — это абсолютно то же самое, что 345 345 = 345 × 7 × 11 × 13. Отсюда следует, что полученное шестизначное число будет делиться без остатка на любой из этих множителей, а потом на два оставшихся.

Благодаря этому математическому факту фокус срабатывает всегда, если вы используете числа 7, 11 и 13. На них будут без остатка делиться любые шестизначные числа из повторяющегося сочетания трех цифр. В заключительной части фокуса, когда вы продемонстрируете ваши поразительные математические способности, просто нужно получить любое шестизначное число такого рода, например 765 765. Конечно, оно будет делиться на 7, 11 и 13. Это неизбежно благодаря все тому же математическому принципу. Таким образом, за фокусом стоит математика, но волшебным его делает ваше выступление.

Выявление закономерности в математике привело к созданию обобщенного правила (математической теоремы), которое используется как алгоритм — в нашем случае для фокуса, а в других ситуациях оно служит основой для программы или разработки аппаратной части. Например, аппаратные модули, выполняющие быстрое умножение, часто используют похожий трюк, основанный на похожей теореме. Числа, записанные двоичным кодом, можно быстро умножить на два, просто сдвинув влево, то есть поставив в конце 0. Фактически никакого умножения не требуется.

Простые множители

Числа 7, 11 и 13 — это простые числа. То есть они делятся только на 1 и на самих себя. Проверьте: ни одно из них не делится на 2, на 3, на 4 и так далее. Эти три числа называются простыми множителями для 1001. Простые множители положительного целого числа — это простые числа, на которые оно делится без остатка.

Древнегреческий математик Евклид открыл, что каждое целое число больше 1, которое не относится к простым числам, можно получить, перемножив простые числа. Более того, для каждого целого числа существует только один набор простых множителей — эта комбинация уникальна. Этот факт называется теоремой о разложении на простые множители или основной теоремой арифметики.

Отсюда следует, что для числа 1001 существуют определенные простые числа, на которых основан наш фокус, — и это единственное такое сочетание. В нашем случае это 7, 11 и 13.

Тестируем математические закономерности

Знание математических закономерностей, лежащих в основе фокуса, поможет нам понять, что будет, если условия изменятся. Например, сработает ли фокус для однозначного числа — например, 3 и, соответственно, 33? Ответ отрицательный. Чтобы удвоить однозначное число, его нужно умножить на 11, а не на 1001. Число 33 — это 11, умноженное на 3. Пока все хорошо, но 11 — это простое число, а значит, оно не делится ни на что, кроме 1 и 11. Больше простых множителей нет. Фокус работает только для 11 и 1, а это слишком очевидно, чтобы казаться волшебным.

Получится ли фокус с удвоенным двузначным числом, например 3434? Ответ снова будет отрицательным, потому что 3434 — это 34, умноженное на 101, а 101 — тоже простое число. Математические знания позволяют нам предсказать, какие закономерности сработают, а какие необходимо проверить.

Вы сделаете фокус еще более надежным, если попросите друга быстро прочитать число вслух и моментально назовете, на что оно делится. Если друг сделает ошибку и, например, скажет 123124, вы сразу же ее исправите, указав на последнюю 4, и все же дадите правильный ответ с быстротой молнии. Это уже будет сопоставление с образцом как часть алгоритма проверки. Вы знаете, что здесь должно быть, и проверяете соответствие. Некоторые программы в системах с особыми требованиями к безопасности осуществляют схожую проверку. Программисты включают в код утверждения, которые являются истинными в момент работы программы в этой точке. Если утверждение неожиданно оказывается ложным, можно запустить специальный код, чтобы разобраться с проблемой. Правильный ввод чисел играет большую роль, и, если люди вводят неверные числа, очень важно, чтобы программа не игнорировала их, но указывала на проблему и давала человеку возможность исправить ошибку (в отличие от нашего фокуса). Это лишь некоторые из многочисленных способов писать надежные программы, чтобы избежать катастроф.

Поиск по запаху: фокус с пахнущей картой

Вот еще один фокус, который кажется невозможным и при этом весьма увлекателен. Чтобы его показать, нужно найти исключение из известной вам математической закономерности, одновременно скрывая его от аудитории. Вы используете способность «находить карту по запаху человека, выбравшего ее». Очевидно, показывая этот фокус, нужно действовать очень тактично!

Попросите зрителя перетасовать карты в колоде. Так на них останется его запах. Потом заберите карты и скажите, что после первой тасовки на некоторых картах остается более сильный запах, чем на других. Вы быстро проходитесь по колоде, обнюхивая карты, и разделяете их на две примерно равные кучки. В одной оказываются карты с сильным запахом — вероятно, их больше касались во время тасовки. В другой — карты вообще без запаха. Вероятно, их пропустили во время тасовки.

Попросите зрителя произвольно выбрать и запомнить одну из карт в стопке с сильным запахом и не говорить вам. Потом зрителю нужно положить ее в стопку без запаха. Вы тасуете эту стопку, а потом снова нюхаете каждую карту. Только по запаху вы можете верно указать карту, которую зритель спрятал в стопке непахнущих карт.

Секретный алгоритм без запаха

Секрет фокуса — обеспечить неочевидную для других закономерность (в разнице между пахнущими и не пахнущими картами) и увидеть исключения из этой закономерности. Здесь для этого используются простые числа. Вы кладете все карты, соответствующие простым числам, в одну стопку, а остальные — в другую. Пусть в нашем случае туз имеет номер 1, валет — 11, дама — 12, а король — 13. Чтобы отделить простые числа, вы кладете 2, 3, 5, 7, валета и короля в одну стопку, а остальные карты — в другую. Поскольку 1 по определению не относится к простым числам, туз отправляется во вторую стопку. Конечно, запах здесь совершенно ни при чем. Вы учитываете достоинство карт и делите колоду по принципу, известному только вам.

Оставшаяся часть фокуса требует от вас всего лишь уверенности и способности увидеть исключение из простой закономерности — это будет несложное упражнение на сопоставление с образцом. Представьте, что в «пахнущей» стопке находятся карты, соответствующие составным числам. Тогда вам нужно искать карту с простым числом в перетасованной «непахнущей» стопке. Для вас она будет выделяться, как огромная блестящая иголка в стоге сена, в то время как зрители будут видеть просто стог.

Конечно, есть и другие шаблоны, чтобы определить разницу между стопками, — например, класть красные карты в одну, а черные — в другую или фигурные карты в одну, а фоски — в другую, однако это слишком очевидно. Такие шаблоны были бы понятны аудитории, и фокус не получился бы.

Увидеть мир таким, какой он есть

Чтобы компьютер видел, важно найти границы

Давайте теперь перейдем к более сложному явлению — возможности компьютера увидеть мир. Для этого мало подсоединить к нему камеру. Компьютер должен уметь определять, что присутствует на картинке, — находить шаблоны и понимать, каким предметам они соответствуют, то есть знать, чтó он видит. Только в этом случае мы и правда сможем утверждать, что он «видит».

Наш мозг постоянно находит шаблоны в изображениях и сопоставляет их с образцами. Свет, поступающий в глаз, преобразуется в сетчатке, которая находится в задней части глазного яблока, в сигналы, идущие в мозг. Эта информация обрабатывается с целью нахождения интересных шаблонов, форм и в конечном итоге предметов. Мы продолжаем узнавать новое о зрении человека, но возможность снабдить компьютер или робота способностью видеть — важная и трудная техническая задача. Она подразумевает разработку алгоритмов, которые обучат компьютеры замечать образцы в увиденном. Одна из фундаментальных способностей человеческого мозга, позволяющая распознавать предметы, — умение находить их границы. Мозг видит линии. Как стало понятно в случае с векторными изображениями, линии — это первый шаг к формам, а затем — к предметам. Так как же «увидеть» линии?

Во-первых, давайте рассмотрим очень-очень скучную картинку (рис. 64a). Как и все компьютерные изображения, она представлена в цифровом виде и состоит из пикселов. Обычно изображение состоит из многих тысяч пикселов. Конечно же, реальный мир из них не состоит! Это просто представление изображения. У каждого пиксела есть присвоенные ему место, особый цвет и яркость. В нашей скучной картинке всего 32 пиксела и два оттенка серого — посветлее и потемнее. Но при взгляде на нее становится ясно, что здесь есть кое-что интересное — вертикальная граница там, где светло-серый с одной стороны сменяется темно-серым с другой. Сама по себе эта граница не является линией пикселов, это всего лишь разница между ними. Мы видим ее только потому, что наш мозг совершает много операций по обработке изображения.

Чтобы написать алгоритм, который позволит компьютеру определить края, необходимо хорошее представление. Изображение легко представить в виде набора чисел, используя разные значения для светло-серого и темно-серого. Благодаря этому мы используем математику в алгоритмах обработки. Условимся, что светло-серый — это число 3, а темно-серый — 4. Например, эти числа могли бы показывать количество чернил, необходимое для печати пиксела. Изображение только из чисел показано на рис. 64b.

Граница никуда не делась, но нам, людям, теперь гораздо сложнее ее увидеть. Она существует только в виде численной закономерности, а мы от природы не обладаем способностью обрабатывать такие закономерности так же хорошо, как изображения. Но, как мы увидим далее, представление облегчит этот процесс для машины.

Теперь давайте посмотрим на еще более мелкий и скучный образец, представленный на рис. 65. Он состоит всего лишь из трех пикселов, однако, надо признать, в нем есть отрицательное число, что делает его немного более интересным. Но как это поможет компьютеру видеть нечто простое? В информатике такой шаблон называется цифровым фильтром. Как и любой фильтр, например в кофеварке, он пропускает лишь нечто определенное. В данном случае — определенные наборы чисел вместо кофе.

Чтобы цифровой фильтр заработал, его накладывают на исходный набор чисел, и элемент за элементом по шаблону умножается на коэффициент. Результаты по всем элементам суммируются, и на выходе получается окончательное значение.

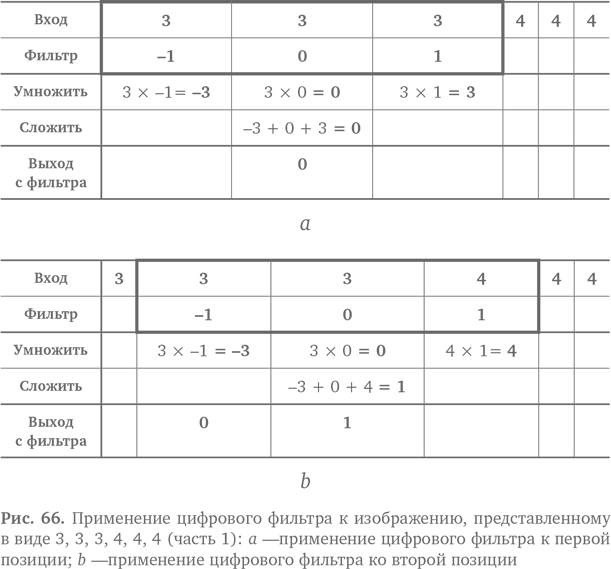
Рассмотрим пример. Допустим, входной набор чисел, представляющий изображение, — 3, 3, 3, 4, 4, 4. Мы применяем к нему фильтр. Как это будет выглядеть для первых трех чисел, показано на рис. 66а. Мы умножаем фильтр на соответствующие числа, получаем −3, 0 и 3, потом складываем их и получаем 0. Это новое значение на выходе фильтра. Теперь фильтр перемещается, словно на конвейере, на один элемент. Он накладывается на новые входные цифры и дает следующий результат на выходе, как показано на рис. 66b. Пожалуйста, двигайтесь дальше! Фильтр сдвигается еще на один шаг, нависает над новыми числами и дает следующий результат. Получается как на рис. 67a. Наконец, передвинувшись еще на один шаг вправо, наш трудолюбивый фильтр доходит до конца, и на выходе появляется последний результат, как на рис. 67b.

Что вообще такое структура изображения?

И где мы оказались после всех этих математических операций? Давайте посмотрим, что у нас есть, не обращая внимания на процесс обработки (рис. 68).

После фильтра на выходе числа оказались больше только там, где была замена значений на входе. Конечно, результат на выходе немного меньше, чем изображение на входе, ведь два значения оказываются пустыми. Однако он гораздо полезнее. Вместо того чтобы считать эти значения на входе в виде цифр, представьте их в виде пикселов. Это картинка.

Теперь подумайте, что происходит, когда вы прогоняете через этот фильтр первую строчку нашего скучного изображения на рис. 64, затем продвигаетесь ниже и проходите следующую, а затем и еще одну строку, пока не отфильтруете все изображение на входе. У вас получится новое изображение немного меньшего размера, как на рис. 69, где мы приняли 0 для белого и 1 для черного. У него есть особое свойства. Все области, где были вертикальные границы, оказались выделенными — они стали линиями. Немного математики, и из исходного изображения возник новый шаблон. Границы превратились в линии, и теперь компьютер их видит.

Программисты изобрели много разных фильтров, каждый из которых может обнаружить в изображениях разные элементы. За этим стоит тот же математический процесс, который мы только что рассмотрели. Правда, сами фильтры становятся все сложнее. Каждый из них — это шаблон. Использование шаблонов в фильтрах является основополагающим элементом компьютерного «зрения» при поиске закономерностей в изображениях. Кроме того, таким образом мы имитируем все, что знаем о человеческом зрении: похоже, что у клеток человеческого мозга есть определенные закономерности восприятия изменений интенсивности света, а это и есть линии.

В наш век перемен все меняется

Важные закономерности проявляются и во времени. Для этого мы создаем ПО, которое наблюдает за людьми, отслеживая выражение лица, и за предметами, которые двигаются и меняются. Для компьютера видео не более чем большой набор чисел. Оно состоит из последовательности картинок, снятых в течение определенного времени, а, как мы уже говорили, каждое изображение — это и есть набор чисел. Чтобы найти в видео интересные вещи, нужно эти числа фильтровать. Можно создать фильтры, которые работают не только во времени, но и в пространстве. Это так называемые временные фильтры — они ищут сходство или различие в значениях пикселов в конкретных участках видеоизображений по ходу фильма. Возьмем фильтр из нашего примера [−1, 0, +1]. Он представляет собой маленькую компактную абстракцию того, что мы хотим найти. У него те же характеристики, что и у границы, — он начинается с меньшего значения и заканчивается наибольшим.

Когда нам нужно проследить за более сложными моделями во времени, мы порой слабо представляем, что это за модели, поэтому трудно создать исходный фильтр. Чтобы решить эту проблему, обычно используют алгоритмы, способные изучить необходимые нам модели. Это подразумевает создание фильтров на основе сотен образцов. Такие фильтры бывают очень сложными. Например, можно взять сотни видео с обычным поведением людей, входящих в поезд метро и выходящих из него, и извлечь из них наиболее вероятные модели. Если прогнать через эти усвоенные фильтры настоящую сцену, происходящую на платформе, они выделят подозрительное поведение. Это могут быть модели движения, которые мы не ожидаем здесь увидеть, — например, кто-то слишком долго ждет у края платформы или на ней стоит сумка, которую никто не забирает. То есть мы увидим исключения из изученных моделей.

Временные модели важны и в музыке. В конечном итоге это, в сущности, и есть музыка — ноты меняются во времени на основе интересных моделей, что доставляет нам удовольствие. Чтобы устранить несовершенства из музыкальной записи, можно использовать фильтры. Например, скандально известное программное обеспечение для «автотюна», которое «исправляет» дребезжащие голоса поп-звезд, и после обработки они звучат безупречно. Программа изучает образец звука, полученный от певца, и образец необходимого звука и меняет вокальный сигнал, приводя его в соответствие с моделью. Программы, распознающие музыку, используют аудиоотпечатки. Это всего лишь образцы звуковых элементов — частота, темп и так далее, — извлеченные из музыкального произведения. Они дают уникальный набор значений — музыкальный отпечаток, который сопоставляют со значениями в объемной базе данных из уже помеченных произведений и таким образом узнают произведение.

В медицине и генетике тоже изучают образцы. Например, чтобы предсказать, какие болезни вероятны для человека, исходя из особенностей его генотипа, или понять, как генетические особенности повлияют на взаимодействие организма с конкретными лекарствами, и адаптировать методы лечения к индивидуальным потребностям. Такое применение информатики и выявление шаблонов открывают перспективы для появления в медицине новых способов, с помощью которых можно находить новые лекарства и новые методы лечения. Например, со временем при поступлении в больницу будут сразу же проводить анализ вашей ДНК, и к тому времени, как вы окажетесь в палате, для вас уже подготовят индивидуальные лекарства, которые гарантированно произведут минимальный побочный эффект лично на вас. Сейчас это уже реальная возможность. Все сводится к тому, чтобы научить компьютеры вычислительному мышлению.

Шаблоны, предсказания, пациенты и тюрьмы

Все перечисленные варианты могут быть очень полезны, но, как мы убедились, программисты должны осознавать, что их алгоритмы и математические ухищрения могут наделить машины способностями, которые можно использовать во вред. Этика, учение о хорошем и плохом, верном и неверном, давно занимает важное место в человеческой философии и истории права. Будет ли создан фильтр, который сумеет по шаблонам, выявленным в информации о человеке, определить, что он собирается совершить преступление? Если да, будет ли правильно арестовать этого человека до совершения преступления? Должны ли присяжные в судах иметь представление о сильных и слабых сторонах математических и вычислительных методов, которые в наши дни все чаще применяют, чтобы выявить предположительно преступное поведение? И если при анализе ваших генов выясняется, что вы, вероятно, заболеете конкретным видом рака, что делать в этом случае? И должны ли страховые компании знать о подобном и требовать больше денег за страховку? Или представьте, что в детстве проанализировали ваши гены и определили, что вы вырастете опасным преступником, — как поступить в этом случае? Все это важные вопросы, на которые сложно дать ответ, но ученые должны играть свою роль в обществе и показывать другим, чем они заняты и как это происходит, — в противном случае сторонние наблюдатели будут воспринимать науку как магию. И хотя волшебные фокусы — отличный способ повеселиться и развлечь других, они точно не подходят для того, чтобы определять развитие нашего общества.

Глава 11
Медицинские чудеса на просвет

Современное здравоохранение опирается на компьютерные технологии и стоящее за ними изощренное вычислительное мышление. Однако, чтобы создать для всего этого основы, нужны усилия математиков и других ученых. Потом программисты и инженеры-электроники разрабатывают алгоритмы и приборы, которые превращают научные достижения в технологии для спасения жизни. Чтобы понять, как это происходит, начнем с игры.

Срез жизни

Морской бой, «Битлз» и части тела

В предыдущей главе мы предположили, что сопоставление с образцом будет играть важную роль в медицине будущего. В этой главе мы рассмотрим некоторые способы, с помощью которых компьютеры, а значит, и вычислительное мышление уже помогают спасать жизнь. В следующий раз, когда будете навещать кого-то в больнице или окажетесь там в качестве пациента, посмотрите вокруг. Палата и вся больница битком набиты продуктами вычислительного мышления. Работа целых отделений в больницах зависит от обработки компьютерами ваших данных. Компьютерная томография, ультразвук, кардио­стимуляторы... в сегодняшнем здравоохранении очень многое существует только благодаря алгоритмам, сенсорам и компьютерным устройствам. И ведь кто-то должен был написать все эти программы, чтобы приборы работали.

Задавались ли вы когда-нибудь вопросом, каким образом врачи получают изображения тела в разрезе? Возможность увидеть, как разные части организма выглядят в поперечном сечении, — важный инструмент диагностики. Но нельзя разрезать человека просто, чтобы заглянуть в него, — нужна технология, позволяющая увидеть, что внутри. История о том, как этот прорыв, за который дали Нобелевскую премию, стал медицинской реальностью, связана с талантливым применением заново открытой математики, компьютерами и рок-группой 1960-х гг.!

Я и моя рентгеновская тень

Рентгеновские снимки — это просто фотографии объектов в рентгеновском излучении, а не в видимом свете. Поскольку рентгеновское излучение проникает сквозь мягкие ткани, но не проходит через более плотные материалы, такие как кости и внутренние органы, с его помощью получают изображение того, что находится внутри тела. Чтобы сделать обычный рентгеновский снимок, вас ставят перед фотографической пластинкой и просвечивают рентгеновскими лучами. В результате на фотопластине получается изображение. Кости, в которых много кальция, обладают более высокой плотностью, чем окружающие ткани, и поэтому поглощают рентгеновские лучи. В результате мы получаем «тень» костей на фотографической пластинке. Хотя этот метод очень полезен, он позволяет понять лишь, сколько костной ткани попалось на пути рентгеновского луча. Как именно кости располагаются в поперечном сечении, непонятно. Тень плоская, а тело объемное.

Цифровые тени

Цифровые рентгеновские изображения в принципе делаются так же. Снимок получают с помощью множества цифровых сенсоров без фотографической (химической) пластины. Даже цифровые рентгеновские аппараты могут давать только плоские изображения внутренних органов. Они сплющивают изображение, лишая его глубины, и оно становится похоже на тень. Однако внутренности трехмерны, поэтому определенно было бы полезно послойно нарезать тело и получить правильное объемное изображение. Это можно сделать с помощью метода компьютерной томографии (от греческого τομή — «сечение» и γράφειν— «писать»). Здесь используются те же рентгеновские лучи, но в томографии источник рентгеновского излучения и детектор вращаются вокруг тела и делают много изображений под разными углами. Это похоже на то, как если бы тело отбрасывало разной формы тени по мере движения солнца вокруг вас. Представьте, что вы исследуете цилиндр с помощью томографии, а источник рентгеновского излучения — факел. Перемещайте факел вокруг цилиндра и смотрите на тень, которая появляется на листе бумаги, находящемся на противоположной от факела стороне. Картинка тени в каждый момент будет одна и та же, потому что цилиндр кругообразно симметричен. Теперь представьте более интересную форму — скажем, чайник. Картинка тени в разные моменты будет зависеть от вашего местоположения относительно предмета. С помощью хитрой математики, алгоритма реконструкции и компьютера вы можете воссоздать форму предмета по изображениям тени.

В томографии это будет форма внутренних органов тела, изображения которых можно записать во всем их трехмерном великолепии. Сейчас существуют системы, в которых излучатель вращается вокруг тела по спирали, что ускоряет процесс. Можно даже снять в разрезе бьющееся сердце и оценить его работу. Математическое основание этой технологии называется преобразование Радона — по имени чешского математика Иоганна Радона, который умер в 1956 г. Оно было разработано как абстрактная математическая теория. В то время никто не видел для нее применения!

Сыграем в морской бой

Игры с карандашом и бумагой

Пока вы думаете, как превратить плоские снимки в трехмерное изображение тела, давайте сделаем перерыв и сыграем в морской бой. Это еще одна простая игра на основе сетки, для которой понадобятся карандаш и бумага. Играют вдвоем. Каждый игрок рисует сетку, помечает на ней ряды и столбцы и решает, в каких клетках расположить корабли. Флот состоит из кораблей разного типа: линкор обычно занимает четыре клетки по горизонтали или по вертикали, крейсер (меньший по размеру корабль) занимает, скажем, только две клетки, а эсминец — одну. Сначала вы решаете, сколько кораблей каждого типа будет в игре, и располагаете их на решетке втайне друг от друга. По правилам вы по очереди «бьете» по решетке вашего противника. Например, противник бьет по позиции В9. Это квадрат в строке B и столбце 9. Если эту клетку занимает часть вашего корабля, он «ранен». Вы должны сказать, какой это корабль, и противник делает следующий ход. Таким образом можно попытаться понять, расположен ли четырехклеточный корабль горизонтально или вертикально. Первый игрок, который потопит весь флот противника, побеждает. Конечно же, труднее всего попасть по эсминцам, которые занимают одну клетку, ведь для этого нужно попасть точно в цель.

Бой в пруду

Теперь представьте гораздо менее масштабную игру, как на рис. 70а. Это скорее не океан, а пруд. В нем только один эсминец (он обозначен цифрой 1 в море нолей) на позиции В2. Может быть, вам повезет, и вы попадете по B2 с первого же выстрела. Но весьма вероятно, что придется долго исключать разные варианты, прежде чем вы его найдете. Есть ли другой способ найти 1?

Я не вижу кораблей, нужна подсказка

Да, такой способ есть, но только если противник даст вам кое-какие простые подсказки. Тогда вы сможете догадаться. Во-первых, нужно, чтобы второй игрок сложил значения клеток в каждой строке и сообщил их. Для ситуации как на рис. 70a информация будет такой: 0 в строке A (потому что там 0 + 0 + 0 + 0, хотя вам скажут только про 0 в сумме), 1 в строке B (потому что там 0 + 1 + 0 + 0) и 0 в строке С. Это начало. Теперь вы знаете, что корабль находится в строке B, но не знаете, где именно. Теперь спросите, какая сумма получается в каждом столбце. В столбце 1 выходит 0, в столбце 2 — 1, в столбце 3 — 0 и в столбце 4 — 0. Теперь вы знаете, что корабль находится в столбце 2. Это показано на рис. 70b, где подсказки расположены в кружочках по краям игрового поля. Обобщив эту информацию, вы поймете, что корабль находится в клетке В2, и — БАБАХ! — он потоплен!

Инструкции по автоматическому поиску кораблей

Теперь представьте, что где-то в сетке располагаются два эсминца. На этот раз мы не скажем, где они. Ваш друг снова сообщает вам сумму значений в каждой строке и столбце. На этот раз вы узнаете, что у вас есть 2 в строке А, 0 в строке В и 0 в строке C; 1 в столбце 1, 0 в столбце 2, 1 в столбце 3 и 0 в столбце 4, как на рис. 71a. Где же корабли?

Вот общий подход к поиску кораблей. Во-первых, нам сказали, что в строке А сумма равна 2. Значит, там что-то есть! Мы можем распространить информацию о присутствии чего-то на всю строку А до самого конца. Хотя мы распределили данные по всей строке, мы все еще не знаем, где находится «что-то», а просто уверены, что оно где-то там есть. Давайте продолжать. Теперь распределим данные по строкам В и С. Здесь нет дополнительной информации, потому что в каждой строке стоит по нолю. В результате получается сетка как на рис. 71b.

Мы знаем, что в строке А что-то есть, это здесь и показано. Но пока мы не знаем, что же это такое. Теперь мы смотрим на столбцы и создаем новую сетку. Если так же распределить информацию по столбцам, где в столбце 1 будет 1, в столбце 2 — 0, в столбце 3 — 1 и в столбце 4 — 0, то получится сетка как на рис. 72a.

Мы знаем, что в столбцах 1 и 3 что-то есть, но не знаем, где именно. Чтобы окончательно решить эту задачу и восстановить расположение кораблей, мы просто складываем эти сетки с распределенной информацией вместе и получаем сетку как на рис. 72b.

В объединенной сетке, например, A1 = 2 + 1 = 3, A2 = 2 + 0 = 2, A3 = 2 + 1 = 3 и так далее. Если теперь посмотреть на эту объединенную сетку с двумя наборами распределенных данных, то мы увидим на ней два пиковых значения 3 на позициях A1 и A3. Эти пиковые значения и отмечают, где находятся корабли. Итак, у нас есть автоматический детектор кораблей, но, что еще важнее, есть и способ открыть истинное расположение кораблей на сетке. Мы можем восстановить, как выглядит наш пруд, по одним подсказкам — см. рис. 73. Чтобы этого добиться, нужно использовать результаты, которые получаются при сложении всех данных в строке и в столбце. Теперь пришло время сняться с якоря и вернуться к рентгеновским лучам. Как вы, вероятно, догадались, все это время мы занимались задачей, связанной именно с ними.

Вернемся к рентгеновским лучам

Рентген укажет место

Рентгеновский луч, проходя сквозь тело, поглощается костной тканью. Поэтому в конкретной точке рентгенографической пластины мы получаем нечто похоже на объединение всех «кораблей» (участки, занятые костной тканью) на пути рентгеновского луча (можно сказать, на строке игрового поля). Итак, наш рентгеновский луч похож на последовательность чисел: строка А = 2, строка B = 0 и строка C = 0. Мы знаем, что луч, поступающий в позицию А, прошел через большее число костей (кораблей), чем лучи, прошедшие через B или C. Но мы хотим знать, как эти кости расположены по отношению друг к другу. Находятся ли они близко или же далеко? В обоих случаях рентгеновское излучение будет поглощено в одном и том же объеме. Но можно вращать источник рентгеновского излучения, как и наш детектор кораблей, вокруг пациента, начиная сверху, а не сбоку, и сделать еще один снимок. На этот раз на рентгенографической пластинке появится информация о форме: колонка 1 = 1, колонка 2 = 0, колонка 3 = 1 и колонка 4 = 0.

Можно взять два рентгеновских луча и объединить полученные данные с помощью операции обратного проецирования, которая называется так потому, что в некотором смысле обратна операции прямого проецирования. Так же, как детектор кораблей мог определить, в какой части сетки игрового поля находятся корабли, эти математические вычисления сообщат вам, где в теле расположены кости. И для этого необязательно делать две сканограммы — при вращении источника рентгеновского излучения вокруг тела получаются сканы различных срезов под разными углами. Затем проводят обратное проецирование и объединяют данные. Таким образом получают высококачественное изображение тонкого среза человеческого тела.

Томограф группы «Битлз»

Этот метод называется компьютерная томография. Первый коммерческий успешный томограф, так называемый «сканер EMI», был разработан для звукозаписывающей компании Thorn EMI еще в 1960-е гг. Рассказывают, что компания финансировала дорогостоящие медицинские исследования на деньги, которые заработала на группе «Битлз» (возможно, самая успешная и влиятельная музыкальная группа за всю историю). Им нужно было потратить огромные деньги! Математические основания обратной проекции существовали уже давно. Однако пока не были разработаны способы их применения в медицине и, что более важно, пока не появились персональные компьютеры, на которых можно было бы производить математические расчеты в разумное время, все эти достижения оставались без внимания и никто не подозревал о связанных с ними революционных возможностях.

Изобретатель «сканера EMI» инженер-электрик сэр Годфри Хаунсфилд совместно с другим ученым был удостоен Нобелевской премии по медицине, а позже за свои достижения возведен в рыцарское достоинство. Сейчас томография постоянно используется в медицине, а еще в археологии — например, чтобы увидеть, как выглядят в разрезе египетские мумии, и в геофизике, чтобы заглянуть внутрь нашей планеты. Это еще один пример того, как математика, техника и программирование, объединившись в нужный момент, могут полностью изменить наш образ действий.

Магниты и модели

Рентгеновская томография позволяет врачам увидеть трехмерные изображения костных тканей, которые поглощают рентгеновские лучи, однако не дает в деталях разглядеть мягкие ткани. К сожалению, именно здесь часто прячется болезнь. В этом случае вместо рентгеновских лучей нужны магниты. На помощь приходит магнитно-резонансная томография (МРТ) и сканеры, предназначенные для этой технологии. С их помощью можно создавать трехмерные изображения мягких тканей, хотя для этого необходимо очень много вычислений.

В МРТ используют явление ядерного магнитного резонанса. Молекула воды состоит из атомов кислорода и водорода, и в ядре атома водорода есть только один протон. Этот скромный протон обладает полезной особенностью. Он действует как мини-магнит, и его ориентация зависит от того, что происходит с протонами в воде вокруг него. К счастью для нас, мягкие ткани человека помимо разных химических веществ содержат много воды. Благодаря этому они и мягкие.

Чтобы сделать снимок тела изнутри, человека, находящегося в сканере, сначала подвергают воздействию постоянного магнитного поля. Это поле ориентирует все протоны тела в одном направлении. Затем к исследуемой области применяется электромагнитное излучение определенной частоты. При этом величина магнитного поля добавляется к исходной. В результате в разных областях тела создается разное магнитное поле. Если воздействовать на протоны нужной радиочастотой, они либо поглотят ее, либо излучат обратно. Частота, на которую отреа­гируют протоны, определяется силой местного магнитного поля. Она, в свою очередь, зависит от плотности протонов и объема мягких тканей.

Эта реакция протонов, поглощающих или излучающих определенную частоту, называется ядерным магнитным резонансом. Резонанс как таковой можно наблюдать в разных природных явлениях. Классический пример — винные бокалы с разным количеством жидкости, которые вибрируют на разной частоте и издают разный звук. Частота, с которой они резонируют, зависит от количества жидкости в стакане.

Магнитный срез

Система МРТ отправляет заранее определенную последовательность радиочастот в исследуемую область тела. Затем она измеряет резонанс, полученный в ответ на каждую из них. Поскольку каждая передаваемая частота настроена на одну из частот в исследуемой области, в результате получается карта, отражающая плотность протонов в разных местах, — то есть карта мягких тканей.

Можно пойти дальше и, используя разную последовательность изображений при разных радиоимпульсах и разных скоростях изменения частоты, вычислить не только объем мягких тканей, но также их тип, а еще данные о химической среде, в которой они находятся. То есть мы получаем для подробного изучения полезные медицинские данные.

С помощью полученных таким образом данных делают, например, объемную пластиковую модель сердца. Хирург может подержать в руках копию сердца, которое ему предстоит оперировать, и заранее точнее оценить сложности, с которыми может столкнуться!

Увидеть в действии

Одно из самых интересных использований МРТ — создание фильмов о процессах, идущих в человеческом теле. Поскольку для этого необходимо подключать большие вычислительные мощности, на обработку уходит довольно много времени. Но несмотря на это, польза очевидна. Например, снимают фильмы о бьющемся сердце, что позволяет медикам увидеть, как открываются и закрываются сердечные клапаны.

Еще интереснее функциональная визуализация. С помощью этого метода, сравнивая снимки разных областей мозга и скорость потребления кислорода, можно увидеть, что происходит в мозге, когда человек думает.

Кровь с высоким и низким содержанием кислорода обладает разными магнитными свойствами. Когда потребление кислорода в какой-то части мозга повышается, мы видим, что именно она задействуется при выполнении определенной задачи. Для изучения этого процесса нам просто нужна контрольная задача, для которой не понадобится конкретная часть мыслительного аппарата, и задача, для которой она понадобится. Если мы «вычтем» друг из друга два цифровых изображения, останутся области, где кислород использовался для выполнения задачи, и с этого момента можно начать исследования работы мозга во время конкретного занятия.

Благодаря чему стало возможно получение таких разновидностей трехмерных снимков? В сущности, в основе лежат математические принципы и научные данные, но именно алгоритмы, а значит, вычислительное мышление превращают записанные данные в полезные изображения.

Еще больше измерений

Тепло и хорошо

Есть и другие способы измерять показатели внутри тела с использованием компьютерных технологий. Человеческое тело предпочитает работать при правильной температуре. Это температура, при которой разнообразные химические процессы идут оптимально, а белки поддерживаются в нужном состоянии. Все это условия поддержания здоровья. Очень важно иметь возможность легко выявить изменения температуры, пульса и других важных показателей, таких как уровень кислорода в крови. Например, если кровь не насыщена кислородом, человек умирает меньше чем за 15 минут. К сожалению, раньше эти тесты проводились очень медленно, и в последнем случае, чтобы определить уровень кислорода в крови, требовалось взять кровь и исследовать ее в лаборатории. Не очень здорово, если жить осталось всего 15 минут. Сегодня эти показатели получают за секунды благодаря сочетанию электроники и алгоритмического мышления, что мы рассмотрим далее.

Полость у нас в голове

Температуру тела легко определить, измерив температуру внутри уха в небольшой и очень полезной полости перед барабанной перепонкой. В эту полость удобно поместить небольшой зонд. Пироэлектрический кристалл в измерительном устройстве подвергается инфракрасному излучению (что означает всего лишь «тепло») со стороны барабанной перепонки. Он создает заряд в соответствии с полученным инфракрасным излучением, а потом этот заряд с помощью специальных алгоритмов преобразуется в показатель температуры.

Дышите глубже

Подобным образом, пульс и уровень кислорода в крови можно измерить с помощью датчика на кончике пальца. Это устройство пропускает сквозь палец световые волны в инфракрасном спектре и регистрирует, сколько поглотила кровь. В крови есть белок гемоглобин, который придает ей красный цвет и, что важнее, доставляет кислород в органы и ткани. Молекулы гемоглобина со связанным кислородом поглощают инфракрасный свет не так, как «ненасыщенный» гемоглобин без кислорода. Трюк, однако, в том, чтобы добавить еще один источник света, который будет светить только красным. Красный свет легче проходит сквозь кровь, полную кислорода, но поглощается, если кислорода нет, то есть происходит обратный процесс. Если использовать их вместе, можно точно измерить количество кислорода. Красный свет с длиной волны 660 нм и инфракрасный с длиной волны 940 нм подаются попеременно. Собранные данные с помощью цифровой справочной таблицы в устройстве (это удобное представление, которое позволяет быстро и легко справиться с задачей) конвертируются в показатель уровня кислорода в крови. Кроме того, это устройство, которое называется пульсоксиметр, позволяет измерять пульс, и этот показатель тоже отображается на экране. Прибор изобрели в 1970-х гг., а в продаже он впервые появился в 1980-х. Сегодня рынок пульсоксиметров оценивается в сотни миллионов долларов.

Высокие технологии и командная работа

Оказавшись в больнице, вы попадаете в мир разнообразных примеров применения вычислительного мышления, что приводит к повышению качества медицинского обслуживания. В медицинских базах данных хранятся история болезни, результаты исследований и выписные эпикризы. Вакуумные повязки с внешним контрольным устройством позволяют заживлять раны снизу вверх. Вживленные умные кардиостимуляторы ежедневно передают в больницу данные о сердечной деятельности пациента и следят за сбоями сердечного ритма, чтобы можно было предотвратить критические ситуации. Все эти технологии работают благодаря компьютерным программам, для создания которых самым активным образом использовалось вычислительное мышление. Но одних алгоритмов недостаточно. Инженерам-электроникам надо было создать сенсоры и прочие устройства. Но еще до этого биохимики и физики должны были изучить, как устроен наш организм, и свойства таких фундаментальных явлений, как протон, рентгеновское излучение и магнитные поля. Понадобились и математики, которые разработали математическую базу для алгоритмов.

Внедряя подобные технологические разработки, надо учитывать один крайне важный момент. Они должны быть такими, чтобы их могли с легкостью применять врачи и медсестры. Это их инструмент, который может как спасти жизнь, так и отнять ее. В больницах всегда много пациентов и напряженная обстановка, что необходимо принимать во внимание при создании медицинских приборов. Следовательно, в процессе разработки должны участвовать психологи и другие специалисты по человеческому фактору. Чтобы совершить настоящий прорыв, который позволит спасать жизни, носителям вычислительного мышления необходимо работать в команде. Они должны использовать достижения многих других специалистов и сотрудничать с ними.

Глава 12
Компьютеры и мозг

Компьютеры точно следуют программам и делают именно то, что написано в инструкциях. Работает ли наш мозг так же, как компьютер? Логичны ли мы? Следуем ли мы своим планам так же точно, как компьютер? Оказывается, у мозга есть весьма серьезные ограничения, которые приводят к довольно странным явлениям. Если понять эти странности, можно усовершенствовать технологии. Однако ясно одно: контролирует происходящее мозг, а не вы.

Думаем как компьютер?

Люди в роли компьютеров

У человеческого мозга и компьютера есть много общего. Наша способность думать, интеллект и самоощущения возможны благодаря тому, что мозг производит массу вычислений. С помощью сложной сети нейронов он обрабатывает информацию, поступающую от органов чувств, принимает решение, что с ней делать, и в результате мы действуем в окружающем мире.

Ученые до сих пор не имеют полного представления о том, как работает мозг, но это неудивительно. В конце концов, в нем приблизительно столько нейронов, сколько капель воды в олимпийском плавательном бассейне. А это очень много!

Сформулируем вопрос следующим образом: думают ли люди как компьютеры, чтобы облегчить себе повседневную жизнь? Похожи ли особенности нашего мышления на вычисления компьютеров? Если мы собираемся заняться компьютерным моделированием жизни, то, чтобы создать роботов, которые бы выживали столь же успешно, как мы, сначала нужно понять, как мы воспринимаем и понимаем мир. Но начнем с другого, хотя и связанного с этой темой, вопроса: естественно ли для нас вычислительное мышление?

Повседневное вычислительное мышление

Как мы знаем, мозг склонен проводить сопоставление с образцом, применяя нечто вроде порождающих правил, — компьютеры часто программируют на это. Мы автоматически реагируем на стимул, следуя заданным правилам. Например, если звонит телефон, я, особенно не задумываясь, подниму трубку. Если в дверь постучат, то я ее открою.

Если посмотреть, как мы, люди, планируем задачи, то окажется, что и здесь мы применяем вычислительное мышление. Например, абстрагирование: мы часто игнорируем детали, чтобы упростить то, чем занимаемся, — разбираясь со сложной ситуацией, мы каждый раз выделяем элементы, которые кажутся нам важными. Представьте, что вы описываете любимый сериал близкому другу. Вероятно, вы опишете не те вещи, на которых сделали бы акцент, если бы надо было написать сочинение на эту тему.

Мы используем декомпозицию, устанавливая цели и подцели, когда составляем план. Например, наша цель — сходить в магазин, чтобы купить еду на неделю. В этом случае у нас будут примерно такие подцели: не забыть взять сумку, заехать в магазин, взять все необходимое, заплатить — и так далее. Цель «взять все необходимое» снова разбивается на подцели. Приехав в магазин, мы, как правило, не задумываемся, где находятся нужные нам товары. И когда мы ищем яйца, нас не интересует, где стоят хлопья для завтрака. Мы делим проблему на отдельные части.

То есть мы применяем вычислительное мышление не только потому, что нас ему научили. Мыслить таким образом для нас довольно естественно, по крайней мере в определенной степени. В то же время информатика учит делать это тщательно и в контексте точных алгоритмических решений.

Вычислительное мышление компьютера

Как мы уже отмечали, сейчас пишется все больше программ, которые позволяют компьютерам не просто заниматься вычислениями, но и мыслить вычислительно. В компьютерных программах тоже используется декомпозиция. Чтобы их было легче писать, разработчики раскладывают инструкции на отдельные шаги или процедуры, так же, как мы разделяем цели на подцели. Это значит, что, продвигаясь к желаемому результату в процессе выполнения инструкций, программа проходит через различные этапы плана, примерно так же, как это делаем мы. Они используют сопоставление с образцом применительно к порождающим правилам, и системы машинного обучения позволяют им увидеть даже более сложные шаблоны. В программах для зрительного распознавания используются фильтры, которые прячут лишние детали, прибегают к своего рода абстракции. Чем больше мы стремимся усовершенствовать искусственный интеллект, тем больше копируем навыки нашего мозга. Как мы видели, знание сводится к вычислению, по крайней мере на уровне нейронов. Так думаем ли мы как компьютеры?

Разница между нашим мозгом и компьютерами может проявиться, если тщательнее рассмотреть, как мы выполняем планы. Вычислительное мышление для нас естественно, однако это не значит, что мы вычисляем так же, как компьютер. Дана ли нам от природы способность выполнять план так же точно, как компьютер? Нет.

Головоломное планирование

Предлагаем вам попробовать вариацию на тему старой головоломки. Она покажет, как люди задумывают и выполняют свои неформальные планы.

Фермерша отправляется в ближнюю деревню с овчаркой по имени Дымка, которую всегда берет с собой. Чтобы попасть в деревню, нужно переплыть реку с быстрым течением. На другом берегу живет изобретательница, которая сделала приспособление, позволяющее быстро перебраться через поток. Оно состоит из веревки, блоков и сиденья для одного человека. Местные жители условились всегда оставлять сиденье со стороны деревни, где живет изобретательница, чтобы она могла каждый вечер убирать его. В конце концов, она ничего не берет за переправу. Добравшись до реки, фермерша перетягивает сиденье с другой стороны. Она садится, прижимает к себе Дымку, перебирается через реку и продолжает путь в деревню.

В один прекрасный день она покупает курицу и мешок зерна. Возвращаясь домой, она приходит на берег и быстро понимает, что у нее проблема. Она может перевезти с собой только что-то одно. Придется переправляться несколько раз. Но если она оставит курицу и зерно на любом берегу, курица склюет зерно. Точно так же, если она оставит вместе Дымку и курицу, собака напугает птицу и та перестанет нести яйца. Но Дымка не ест зерно, значит, его можно спокойно оставить с ней.

Запишите последовательность шагов (конечно, это будет алгоритм!), которую нужно пройти фермерше, чтобы переправить всех и вся в целости и сохранности и продолжить путь. Помните, что собака и курица, а также курица и зерно не должны оставаться без присмотра.

Сначала решите головоломку, а потом читайте дальше.

Автоматические ошибки

Мы, люди, делим выполняемые задания на подцели, но, как выяснилось, в отличие от компьютеров, мы обычно забываем о подцелях и не заботимся о последствиях. Это происходит потому, что объем нашей краткосрочной памяти ограничен. Если в настоящий момент нам надо запомнить слишком много, то неизбежно что-то упустим из внимания, так как концентрируемся на более важном. Что ваш мозг считает самым важным? Приоритет получают цели, которых вы хотите достичь, в отличие, например, от необходимости навести порядок. Вряд ли вы забудете включить свет — без этого будет не видно, что вы делаете. Однако легко забыть его выключить перед уходом. Почему? Потому что вы достигли своей цели в комнате и ваш мозг переключился на новую важную цель — ту, ради которой вы уходите из комнаты.

Как это применимо к нашей головоломке? Дело в том, что многие находят ответ и у них получается переправить фермершу, собаку и зерно через реку. Однако они упускают последний шаг — не возвращают сиденье на другой берег. Правильное решение представлено на рис. 74.

Если этот последний шаг не включен в ваш план, значит, вы допустили в своем алгоритме то, что называют ошибкой после выполнения. Вы сосредоточены на цели, но забыли, что после выполнения подцели нужно кое-что доделать, то есть вы сделали ошибку на стадии планирования. Еще проще забыть что-то вроде этого, занимаясь повседневными делами. Мы не совершаем подобных ошибок каждый раз, когда для этого создаются условия. Все зависит от того, как много еще надо удержать в голове. Если краткосрочная память заполнена другим, вероятнее всего, вы забудете о подобных завершающих задачах. Краткосрочная оперативная память индивидуальна, поэтому некоторые делают такие ошибки чаще. Но если в голове нужно держать достаточно много, рано или поздно их делают все.

Так что, по крайней мере в этом отношении, мы не похожи на компьютеры. Они четко следуют плану. Нашему мозгу трудно это сделать без помощи.

Машина протягивает руку помощи

Итак, мы делаем ошибки, но машины могут помочь их избежать. Банкоматы на улице — хороший пример того, как программирование позволяет повысить или снизить вероятность такого рода ошибок. Когда они только появились, вы получали деньги, а потом карту (в некоторых странах это до сих пор делается так). Выяснилось, что многие люди уходили с деньгами, но без карты. Почему? Потому что у них была цель — взять деньги. Как только главная цель была достигнута (пришли и получили деньги), они уходили, мысленно уже обращаясь к следующей цели. Предыдущая подцель — вставить карту — выполнена и забыта... а вместе с этим забыта и появившаяся новая подцель — забрать карту.

Решение для этой конкретной «ошибки после завершения» оказалось простым. Программист написал для банкомата код, в соответствии с которым он не выдает наличность (ваша цель), пока вы не заберете карту (не выполните завершающую подцель). Таким образом, вы вынуждены кое-что доделать (подцель), прежде чем достичь цели. Так сейчас работают банкоматы в Великобритании. И это не единственное решение. Например, на бензоколонках карту просто прокатывают — то есть вам вообще не нужно ее куда-то вставлять. Хорошая проработка помогает преодолеть недостатки в обработке информации, свойственные нашему мозгу, но без посторонней помощи мы делаем ошибки. В этом случаи машины должны помогать. К сожалению, урок не был усвоен в более общем плане! Когда магазины начали вводить кассы самообслуживания, вдруг обнаружилось, что многие, оплатив покупки, забывают карты. Обобщенное решение было проигнорировано.

Потеря карты, ее блокировка и получение новой — досадные неудобства, но подобные недостатки могут быть запрограммированы в самых разных устройствах. Как мы знаем, больницы набиты чудесами техники, которые помогают спасать жизнь, но плохая конструкция может привести к тому, что жизнь оборвется. Например, медсестры должны настраивать инфузионные насосы для вливания. Эти устройства могут иметь тот же недостаток, что и банкоматы. Настраивая их, необходимо закрывать зажим, чтобы прекратить поступление лекарства. Но как только компьютер настроен на верную дозу, зажим надо открыть. Это как раз тот самый шаг, о котором легко забыть. А медсестры должны помнить и делать гораздо больше, чем вы, когда стоите у банкомата. Это как раз те ситуации, когда машина должна помогать, а не препятствовать.

Качественное вычислительное мышление означает проектирование компьютеров, которые помогают преодолеть «недостатки», мешающие нам думать как компьютер.

Игра с несовпадением. Невозможное ограбление

Сбивая со следа

Нашему мозгу приходится иметь дело с различными ограничениями в работе, а не только с конечным объемом краткосрочной памяти. Кроме того, у него нет полного понимания ситуаций, и, чтобы достаточно быстро реагировать на окружающий мир, ему необходимо обрабатывать большие объемы информации, которые поступают от органов чувств. Оказывается, в ходе этого процесса мозг делает много разных ошибок.

Как мы видели на примере с банкоматом, если понять, какого рода ошибки делают пользователь, можно создать системы (компьютерные и другие), которые смогут их не допустить. Конечно же, порой мы заинтересованы в том, чтобы люди делали ошибки и принимали ошибочные допущения, не имеющие оснований, — на этом и строятся фокусы. Итак, давайте на примере фокуса посмотрим, как человеческий мозг старается увидеть подлинную реальность и промахивается там, где у компьютерного мозга проблем не возникает.

Мы знаем, что сосчитать пять монет слева направо — абсолютно то же самое, что сосчитать их справа налево. Однако если мы создадим систему, которая намеренно введет некое несоответствие, при котором два предположительно одинаковых явления не совпадают, а зритель этого не замечает, то можно организовать довольно интересный фокус, навязав ошибку, свойственную человеку.

Невозможное ограбление

Покажите другу классический сюжет фильма. Как во всех хороших фильмах об ограблениях, в конце будет неожиданный поворот. Герои и реквизит — это два вора и пять драгоценных камней. Их играют одинаковые небольшие монеты, всего семь. Две монеты представляют воров, а остальные пять — драгоценные камни.

СЪЕМКА «ИЗ ЗАТЕМНЕНИЯ». История начинается с того, что пять драгоценных камней выкладывают в прямую линию на столе.

СЦЕНА 1. Два вора, которых изображают две монеты, по одной в каждой руке, как это обычно бывает в фильмах об ограб­лениях, спускаются с потолка на веревках. Вы изображаете это, держа руки над столом. Сначала вы показываете монеты в руках, потом сжимаете кулаки и опускаете руки. Теперь воры собирают драгоценные камни — вы по очереди поднимаете по камню (монете) со стола обеими руками и зажимаете их в кулаках, пока не заберете все.

СЦЕНА 2. Драматичный момент. Должно быть, последний камень выскользнул, и включилась сигнализация. Охранник вот-вот подойдет, поэтому воры быстро возвращают камни на стол — один за другим. А потом поднимаются на веревках на безопасную высоту, чтобы их не засекли. Уловка срабатывает. Охранники видят все пять камней на месте, отключают и снова включают сигнализацию и уходят, не потрудившись посмотреть вверх.

СЦЕНА 3. Два вора спускаются и снова и по одному забирают драгоценные камни. Кажется, это сойдет им с рук. Но вот финальный поворот сюжета: охранник замечает воров, когда они уже готовы убежать по крыше, и начинается схватка, которую вы демонстрируете, тряся кулаками над столом. Схватка заканчивается, вы театрально разжимаете кулаки, и два вора удивительным образом оказываются в одном, а пять камней — в другом.

ЗАТЕМНЕНИЕ. В невозможном ограблении происходит загадочный и неожиданный поворот — но как это провернули?

Понадобились спецэффекты, вычислительное мышление и когнитивные искажения. Давайте посмотрим, что осталось за кадром.

Что происходит за кулисами?

В этом классическом фокусе с монетами скрыт хитрый алгоритм, который применяется вместе с красивой манипуляцией восприятия зрителей, и в результате получается невозможный на первый взгляд финал. Фокус показывается в точности как описано выше, шаг за шагом, однако мы не упомянули одну очень важную деталь. В нем используется несоответствие: аудитория считает, что монеты находятся в одном состоянии, однако на самом деле это не так. Здесь важно, как вы поднимаете монеты или заменяете их на столе. Каждый раз, когда вы берете монеты со стола, вы начинаете справа. То есть правая рука берет монету крайнюю справа, в то время как левая рука берет монету крайнюю слева — и так далее. Число монет нечетное. Таким образом, после первой последовательности «справа — слева» в правом кулаке остаются четыре монеты (вор и три драгоценных камня) и в левом кулаке — три монеты (вор и два камня).

Но во время второго эпизода вы возвращаете камни назад, начиная слева и левой рукой, то есть, когда на столе снова оказываются пять монет, у вас остается две в правой руке и ни одной — в левой. Однако здесь-то и срабатывает несоответствие. Зрители полагают, что вы вернулись к началу и все камни лежат на столе, а в кулаках — по одному вору. Ваша задача — убедить их в этой ложной реальности, конечно, не разжимая кулаки. Итак, вы просто рассказываете историю, сообщая, что оба вора вернулись туда, где были, и взлетают вверх на веревках, чтобы спрятаться.

В третьем эпизоде мы снова поднимаем камни со стола, и процесс начинается справа. Мы берем камень правой рукой, и после знакомой последовательности «слева–справа» фокус для вас заканчивается, потому что в правой руке у вас пять монет, а в левой — две. В итоге вы сообщаете, что это два пойманных вора и пять возвращенных камней.

Прячем алгоритм кражи и смену состояний

Последовательность, в ходе которой мы собираем монеты слева направо, потом возвращаем их справа налево и снова собираем слева направо, — это алгоритм. Он гарантирует, что все состояния кулаков (сколько в каждом монет) полностью соответствуют условиям, необходимым, чтобы фокус получился.

Однако неспособность зрителей заметить это несоответствие, подкрепленная историей, которую вы рассказываете, ослабляет их шансы проследить за реальной последовательностью состояний. Трюк подкрепляется нашей склонностью запоминать информацию так, чтобы это подтверждало уже сложившиеся убеждения (заданные фокусником). Это называют склонностью подтверждать свою точку зрения. Оглянувшись в прошедшие события, зрители вспомнят, что вы просто поднимали и клали монеты, а эти два действия оставляют вас там же, где вы начали. Это убеждение основано на опыте из реального мира, где, например, мы выкладываем вилки на стол, а потом берем их и кладем обратно, и это не дает абсолютно никакой разницы в числовом выражении. Так оно и есть — в большинстве случаев разницы не будет. Однако с помощью хитрых алгоритмических манипуляций с изменением состояний можно получить магический эффект.

Итак, мы нашли еще одну ситуацию, в которой наш мозг некоторые ситуации воспринимает неправильно. Мы стараемся следить за происходящим в мире, делая догадки вместо того, чтобы внимательно следить. Наши догадки часто подтверждают то, что мы считаем правдой, и не всегда — происходящее на самом деле.

Вдохновение из прошлого

Вариант фокуса с ограблением был придуман специально для этой книги, но, конечно же, алгоритм можно спрятать за какой-нибудь другой историей в вашем стиле. Основа трюка существует давно, но сегодня его обычно показывают с помощью монет и рассказывают при этом об овцах и ворах. Руки фокусника — это два сарая, в каждом из которых сидит по вору. В соответствии с механикой трюка маг по очереди подбирает пять монеток-овец обеими руками. В конце оба вора волшебным образом оказываются в одном «сарае», а «овцы» — в другом. Раньше для фокуса использовали самые разные темы — например, «Овцы и волки», «Полицейские и грабители», «Лисы и гуси» или «Браконьеры и кролики». Его показывали с помощью бумажных шариков, спичек и других мелких предметов. Многие фокусники создали свои варианты этого трюка. Если вам интересна эта тема, о ней можно прочесть в книге Дж. Бобо «Современные фокусы с монетами» (Modern Coin Magic) и заодно узнать кое-что полезное о манипуляциях с помощью ловкости рук и других фокусах, которые удивят ваших друзей.

Мир иллюзий

Можно ли положиться на органы чувств?

Компьютеры получают данные от сенсоров, будь то фотоэлемент, нажатая клавиша, GPS или акселерометр. Эти данные — непосредственные измерения, сделанные в физическом мире. Они представляют собой электрические сигналы в вольтах или амперах, и при правильной настройке сенсоров мы точно знаем, что означают результаты этих измерений.

У людей пять довольно точных органов чувств, которые отвечают за зрение, вкус, осязание, обоняние и слух. Но можно ли утверждать, что органы чувств работают по тому же принципу, что и сенсоры в компьютерных устройствах? Или же они устроены сложнее — но в таком случае как? Чтобы исследовать этот вопрос, необходимо погрузиться в мир иллюзий. Вы, конечно же, знакомы с оптическими иллюзиями — этими чарующими картинками, на которых прямая линия кажется кривой, два одинаковых предмета выглядят так, будто они разного размера, и так далее.

Благодаря этим иллюзиям мы знаем, что глаза работают не так, как простая камера на смартфоне. Они обрабатывают информацию до того, как мы ее используем, и в некоторых случаях дают неправильные измерения физического мира. А как работают другие органы чувств? Приведем примеры простых иллюзий, которые легко показать с помощью предметов, имеющихся у вас дома. Результат вас поразит.

Иллюзия сладости

Наше восприятие вкуса зависит не только от того, что мы пробуем. В частности, сладость сахара зависит от его температуры. Попробуйте сделать так. Размешайте сахар в миске с водой. Потом налейте половину жидкости в один стакан и поставьте его в холодильник. Остатки налейте в другой стакан и оставьте его рядом с батареей отопления. По научным данным, воспринимаемая сладость сахарозы (сахара) повышается на 40%, когда температура повышается с 4 ˚С (приблизительная температура холодильника) до 36 ˚С (приблизительная температура тела). Возьмите оба стакана с водой, предложите другу попробовать и спросите, в каком из них вода слаще (конечно, доля сахара в обоих абсолютно одинакова). Если друг скажет, что теплая вода слаще, у вас получится иллюзия сладости.

Если вы хотите применить по-настоящему научный подход, сделайте еще сладкой воды и разлейте ее поровну по четырем стаканам. Поставьте один в холодильник и второй у батареи, а еще два оставьте в комнате. Два стакана с водой комнатной температуры будут контрольными в нашем эксперименте. Попросите друга попробовать, насколько сладкая вода в двух стаканах комнатной температуры. Поскольку и температура, и доля сахара у них одинаковы, вода должна восприниматься как одинаково сладкая. Контрольные стаканы покажут, что эффект действительно создается благодаря температуре, а не, например, из-за того, что вода в первом стакане, из которого мы пьем, всегда кажется слаще.

Чтобы эксперимент был еще более научным, попросите друга сполоснуть рот чистой водой между дегустациями. В этом случае образцы не будут загрязнены.

Иллюзия температуры

Теперь познакомимся с иллюзией температуры. Возьмите три стакана воды, поставьте один в холодильник, наполните другой теплой водой из-под крана (именно теплой, а НЕ горячей), а в третий налейте обычную холодную воду, тоже из-под крана.

Поставьте три стакана в ряд в следующем порядке: теплая вода, вода комнатной температуры и холодная. Опустите палец одной руки в теплую воду и палец другой — в воду из холодильника. Подержите их так недолго, а потом опустите оба пальца в стакан с водой комнатной температуры. Пальцем, который был в теплой воде, вы почувствуете холод, а пальцем, который был в очень холодной воде, — тепло, хотя оба находятся в одном и том же стакане.

Произошло следующее: когда ваш палец был, скажем, в теплой воде, он приспособился к температуре этой воды. Ваше тело интересует только то, что изменяется в окружающей среде, потому что на эти изменения нужно реагировать. Поэтому, после того как ваш палец приспособился к теплой воде, при погружении в стакан с водой комнатной температуры он «рассчитывает», что вода будет теплой. Но когда оказывается, что это не так, мозг приходит к выводу: «Вода не теплая, значит, она холодная». Подобным образом палец в воде из холодильника привыкает к холоду, а когда он оказывается в воде комнатной температуры, делается вывод: «Вода не холодная, значит, теплая».

Иллюзия прикосновения

Если порыться в ящике с инструментами, можно найти материал для простой иллюзии — иллюзии наждачной бумаги. Осторожно потрите одну руку мелкозернистой наждачной бумагой, а другую — грубой. Теперь потрите обе руки наждачной бумагой со средним зерном. Ощущения в каждой из них будут разными. Почему? Потому что рука, которую потерли мелкозернистой наждачной бумагой, адаптировалась к легкой шероховатости, а рука, которую потерли крупнозернистой, адаптировалась к очень сильной шероховатости. Как и в иллюзии с температурой, когда руки приспособили осязательные ощущения к разной степени шероховатости, средний вариант будет ощущаться по-разному. Предскажите, используя объяснения иллюзии температуры, какая рука будет ощущать среднезернистую бумагу как более грубую. Потом проведите эксперимент и посмотрите, верна ли ваша догадка.

Иллюзия веса–размера

Эта иллюзия была впервые описана более ста лет назад. Если вы поднимете два предмета одинакового веса, вам покажется, что предмет меньшего размера тяжелее. Возьмите две пустые пластиковые бутылки разного размера и с помощью весов налейте в них одинаковое количество воды. Попросите друга взять их и спросите, какая тяжелее. Если друг ответит, что тяжелее маленькая бутылка, значит, вы наблюдаете иллюзию веса–размера. Можно даже сообщить, что оба предмета весят одинаково. Иллюзия сохранится.

Но этим странности не ограничиваются! Исследователи обнаружили, что, когда люди попеременно поднимают предметы одинакового веса, но разного размера, усилие в кончиках пальцев оказывается одинаковым, несмотря на иллюзию веса–размера. Одна часть мозга оказывается обманутой и сообщает, что они разные, в то время как другая знает правду. Но эти части не взаимодействуют друг с другом!

Оптическая иллюзия

Поскольку мозг обладает внушительной мощностью для обработки информации, поступающей от органов чувств, большую часть времени мы хорошо осознаем, что важного происходит в окружающем мире. Эти эксперименты получаются, поскольку они, учитывая особенности обработки информации мозгом, специально рассчитаны на то, чтобы заставить его ошибиться.

Но что происходит, когда источник данных об окружающей среде плох или слишком много помех? В этом случае мы испытываем особую иллюзию под названием парейдолия. Она возникает, когда нечеткий произвольный стимул (часто картинка или звук, например, плохо настроенного телевизора или радио) воспринимается как имеющий конкретный смысл. Мы видим животных или лица в облаках или слышим несуществующие скрытые послания на пластинках, проигрываемых наоборот.

Возможно, вам никогда не приходило в голову, что мозг сам изобретает кое-что из того, что вы «видите». Слепое пятно на сетчатке глаза — место, где зрительный нерв, по которому световые сигналы идут в мозг, отходит от глазного яблока. В этом месте вообще нет светочувствительных рецепторов, а значит, эта часть сетчатки физически не может ничего увидеть. Так почему вы абсолютно не ощущаете наличие этого овального участка без рецепторов диаметром около 1,5 мм? Оказывается, пустое место заполняет мозг. Он сам создает информацию, которая позволяет это сделать. Это своего рода заполнение имеет весьма изощренный характер и зависит от того, что мы наблюдаем в окружающем мире вокруг слепого пятна. Например, закройте левый глаз и смотрите правым на + на рис. 75. Теперь придвигайте и отодвигайте от себя страницу, пока X не попадет на слепое пятно. Мозг заполнит пустое место непрерывной прямой линией.

Итак, даже если ничего нет, мозг ищет знакомые и ожидаемые шаблоны. И при их отсутствии он их просто создает.

Математическая модель сознания

Закон Вебера–Фехнера

Как физический мир влияет на наши органы чувств? Это глубокий вопрос, очень важный для человеческого опыта, который беспокоит философов уже многие века. Мы ощущаем физический мир вокруг нас: глаза определяют интенсивность света, ухо чувствует изменения в атмосферном давлении, кожа — изменения в давлении на нее, нос ощущает присутствие химических веществ в воздухе, а язык — в пище. Но как вся эта физическая стимуляция на самом деле переходит в ощущение веса, восприятие слов, удовольствие от вкусной еды? Как определение характеристик стимула организмом переходит в мозге в опыт восприятия?

У нас до сих пор нет ответа на этот вопрос, но еще в 1860 г. немецкий доктор по имени Эрнест Генрих Вебер вместе с коллегой Густавом Фехнером открыл нечто крайне интересное. Существует простое математическое правило (скорее уравнение, чем порождающее правило), которое показывает, как соотносятся интенсивность раздражителя и интенсивность восприятия. Правило называется закон Вебера–Фехнера. Оно применимо к самым разным ощущениям и является одним из первых примеров математической модели, отражающей отношение тела к разуму. Вебер проводил эксперименты, а Фехнер нашел математические обоснования этого закона.

Увесистый психологический эксперимент

Вебер провел несколько классических экспериментов, которые помогли вывести это правило. Он завязывал человеку глаза и давал ему в руку предмет определенного веса. Затем постепенно добавлял вес до тех пор, пока человек не чувствовал, что вес увеличился. В данном случае вес предмета представлял собой интенсивность раздражителя, а способность человека ощущать изменения позволяла измерить разницу в интенсивности восприятия.

Вебер обнаружил, что добавочный вес, который можно увеличивать до тех пор, пока человек не почувствует разницу, зависит от исходного. Если в руке было лишь 10 г, то был заметен добавленный 1 г. Если же основной вес составлял 1 кг, то добавление 1 г не воспринималось. Такого рода эксперимент, когда вы манипулируете чем-то в физической реальности и измеряете восприятие, называется психофизикой, и Вебер с Фехнером стали пионерами в этой области исследований.

Выразим математически

Закон Вебера–Фехнера имеет следующую формулировку: чем сильнее исходный стимул, тем больше должны быть изменения, чтобы мы их заметили. Слова всегда полезны, и Вебер описал свои открытия, а Фехнер на основе данных экспериментов нашел для них удивительно простое математическое описание.

Условимся, что сила стимула — S. Например, в описанном случае это будет основной вес предмета в руке. Предположим, что мы заметим изменения, только если повысим интенсивность стимула на dS (помните, что dS — это добавленный и воспринятый вес). Согласно закону Вебера–Фехнера, если разделить добавленный вес на основной вес, мы всегда получим одно и то же число

dS/S = k,

где k — константа. Это число, получаемое из экспериментальных данных.

Предсказываю, что...

Если измерить константу k для конкретного веса (проведя измерения и выполнив деление), то можно проверить, сохранится ли она для других весов. И, что еще лучше, можно высказать предположения и проверить их. Представьте, что мы делаем это для низкого основного веса 10 г, при котором чувствуется, когда он повышается всего на 1 г. Закон Вебера говорит, что 1 г / 10 г — это константа. В данном случае — 0,1. Используя эту экспериментальную константу 0,1, мы можем предсказать, какой вес надо добавить (dS), если основной равен 1 кг (1000 г). Закон утверждает, что (dS / 1000) равно 0,1. Если подставить в формулу новое значение, она будет выглядеть так:

dS = 0,1 × 1000 = 100 г.

С помощью математических вычислений мы сделали предсказание о соотношении телесного и умственного восприятия, которое теперь можно протестировать. Если бы мы использовали только словесное описание, то не смогли бы получить такую возможность для тестирования.

Полезное универсальное правило

Исследователи в области психофизики выяснили экспериментальным путем, что если не ударяться в крайности, то закон Вебера хорошо позволяет предсказать, как интенсивность раздражителя соотносится с интенсивностью восприятия. Закон справедлив для веса, яркости света, громкости звука и даже длины линий. У него много применений в вычислительных системах — например, в компьютерной графике, при демонстрации изображений и обработке звука. Еще его используют, когда надо решить, что именно стоит демонстрировать на маленьком экране. Зачем показывать деталь, которую никто не заметит из-за бросающихся в глаза элементов вокруг нее? Подобным образом, если вы хотите сжать звуковой файл и сэкономить место на его хранении, можно использовать алгоритмы на основе закона Вебера, чтобы понять, какие элементы звука можно удалить и этого никто не заметит. Например, тихие звуки на фоне очень громких.

Закон Вебера–Фехнера можно наблюдать повсюду вокруг нас, хотя, вероятно, вы этого не замечали. Спросите себя: почему вы не видите звезд днем? Они светят так же ярко, как и ночью. Почему вы не замечаете тиканья часов в шумное дневное время, но всегда слышите его в ночной тишине? Все это закон Вебера–Фехнера, который работает изо всех сил, помогая нам предварительно обрабатывать и искусно сжимать данные, поступающие в мозг. Мозг делает это, чтобы мы могли справиться с гораздо большим объемом вводных данных, чем если бы мы, как механический сенсор, просто измеряли непосредственно стимулы.

Имитируем биологию на благо технологий

В ходе эволюции были найдены талантливые решения сложных технических задач и проблем в области обработки информации (но ни разу не патентовались). В настоящее время активно развивается биомиметика — область компьютерных наук, которая занимается изучением принципов функционирования биологических систем, чтобы, поняв их, внедрить в компьютерные системы. Таким образом можно проверить, добились ли мы желаемого, то есть обладает ли компьютерная система свойствами системы природной. А это означает, что мы можем прогнозировать, и кроме того получить очень полезные алгоритмы для усовершенствованных компьютерных программ. Естественные науки, компьютерные науки и информатика идут рука об руку.

Специалисты по компьютерным наукам черпают вдохновение в природе и создают алгоритмы, которые помогают нам выполнять сложные задачи. В процессе естественного отбора появились умные инженерные решения, которые позволили живым существам выжить на нашей планете. Так почему бы их не скопировать? В конце концов, крылья птиц подсказали первым авиаторам идею аэроплана. Так зачем на этом останавливаться? В ходе эволюции были не только решены инженерные проблемы, но и нашлись способы обработки информации для решения очень сложных задач.

Ученые-компьютерщики изучили, как работает наша иммунная система со сложной системой антител, которые позволяют справиться с болезнью. Антитела подбираются так, чтобы их форма соответствовала форме белковых молекул на поверхности микробов и других угрожающих здоровью организмов. Систему антител можно сымитировать на компьютере и ввести в алгоритм набор различных цифровых шаблонов. Так мы выявим шаблоны в данных, будь то вербальный контент, спам-сообщения или подозрительный трафик в сети.

Компьютерная симуляция путей муравьев-фуражиров, доставляющих добычу в муравейник, используется, чтобы помочь роботам разработать хорошие решения по улучшению своей навигационной схемы. Изучение системы зрительного внимания, которая показывает, какие участки изображения привлекают наш взгляд, и создание ее модели стали возможными благодаря пониманию принципов работы зрительной зоны коры головного мозга, отвечающей за обработку визуальной информации. С помощью этой модели роботы начинают понимать, что происходит перед ними, а специалисты по рекламе улучшают дизайн своих макетов.

Постоянное продвижение в понимании принципов работы биологических систем позволит компьютерам работать по-но­вому, в основе схем будет лежать упрощенный вариант систем, функционирующих в природе.

Предубеждения мозга

Трюк уличного фокусника: быстро загадайте число

Уличные фокусники часто используют этот психологический трюк. Попросите друга быстро загадать двузначное число от 1 до 100, из нечетных и обязательно разных цифр. Сосредоточьтесь и дайте ответ… 37!

Магия: статистический фокус с угадыванием числа 37

Во-первых, этот фокус получается не всегда! Конечно, в телепередачах показывают только случаи, когда он удается. Фокус основан на вероятности и довольно хитром способе ограничить выбор зрителя. Если он не сработал — о чем разговор! Это же чтение мыслей — дело сложное. Просто вы не настроились как следует.

Как это работает?

Вы сообщаете добровольцу, что он может выбрать любое дву­значное число между 1 и 100. Значит, он запомнит, что него есть выбор в промежутке от 1 до 100. Это так называемый эффект первичности при запоминании: мы лучше запоминаем то, что было в начале.

Потом вы говорите, что обе цифры должны быть нечетными, и это сокращает возможные варианты в два раза — исключаются все четные. Потом вы говорите, что цифры должны быть разными, и это еще больше сокращает выбор. По факту остается очень мало чисел, из которых можно выбрать (хотя обычно никто этого не замечает).

И здесь настает черед психологии и статистики. Когда людей просят быстро выбрать число, огромное большинство называет 37. Возможно, дело в том, что оно стоит где-то посередине. Число 13 слишком мало, 97 — велико. Может быть, люди просто объединяют 3 и 7, которые чаще всего выбирают, если задан промежуток от 1 до 10. Как бы там ни было, велики шансы, что вы получите желаемое число 37.

Психология, искажения и когнитивистика

Эффект, вследствие которого большинство людей выбирают число 37, называется когнитивным искажением. Вот еще один пример: если попросить быстро выбрать любой цвет, большинство людей назовет КРАСНЫЙ. А если речь зайдет об овоще, большинство подумает о МОРКОВИ. Такие особенности человеческой психологии, например первичный эффект при запоминании и когнитивные искажения, использованные в описанном фокусе, изучает когнитивистика. Это увлекательная наука, которая пытается понять процесс человеческого мышления. Специалисты по вычислительным системам используют ее достижения, чтобы создавать легкие в использовании программы или искусственный интеллект со способностями, подобными человеческим. Поэтому в следующий раз, когда вам придет в голову 37, вспомните об открытиях когнитивистики и выберите 57 (а может быть, вы так и поступили!).

Кругом одни искажения

Если подбросить симметричную монету 10 раз подряд и каждый раз выпадет решка, какова вероятность, что в следующий раз будет орел? Считаете, что вероятность этого высока? Вовсе нет. Всякий раз, когда мы подбрасываем монету, шансы 50 : 50, и эта вероятность не зависит от других попыток. Но большинство людей в такой ситуации уверены, что решка обязательно появится, хотя за этим убеждением не стоит рациональных вероятностных аргументов. Такое когнитивное искажение называется ошибкой игрока. Мы склонны считать, что на будущую вероятность какого-то события влияют предыдущие события, тогда как в реальности такой зависимости нет.

Если подробно рассмотреть, как люди действуют индивидуально и в группах, то выясняется, что мы часто не принимаем рациональные решения. И в отличие от компьютера мы не выполняем логические и математические правила. Как мы уже отмечали, индивиды совершают когнитивные ошибки — как в случаях с монетой или числом 37. Также мы знаем, что по закону Вебера–Фехнера мы можем эффективно сжимать информацию, поступающую от органов чувств.

Когда много людей объединяется, то в процессе обработки информации появляются очень странные эффекты когнитивного искажения. Возможно, это отголоски нашего далекого прошлого, когда мы были охотниками и собирателями с племенной ментальностью, которая наряду с социальными сигналами, помогающими выбрать партнера, позволяет сформировать тесно сплоченные группы. Однако это часто приводит к проблемам. Давайте посмотрим, о чем идет речь.

Например, эффект обратного результата проявляется, когда люди сталкиваются с доказательствами, опровергающими их убеждения, но, как ни странно, их вера только укрепляется! Эффект присоединения к большинству — тенденция, присущая нам, действовать так же, как другие. Добавьте к этому склонность подтверждать свою точку зрения, которую мы рассмотрели выше, и вы увидите, что наш собственный мозг порой сильно мешает докопаться до истины.

Но мозг позаботился и об этом: у нас есть встроенное слепое пятно в отношении когнитивных искажений. Нам кажется, что у нас меньше предубеждений, чем у других. Мы видим у других больше когнитивных искажений, чем у себя самих. Способность учиться тоже находится под влиянием искажений. Социальные психологи Дэвид Даннинг и Джастин Крюгер обнаружили, что недостаточно компетентные индивиды часто переоценивают свои навыки, а специалисты — недооценивают.

Когнитивные искажения можно использовать, чтобы стать популярнее. Эффект ореола подразумевает, что в наших глазах положительные и отрицательные качества человека переходят из одной области в другую. Это ярко проявляется в случае с привлекательными людьми. Нам кажется, что они обладают достоинствами, которых на самом деле нет, — просто потому, что эти люди красивы. Когда мы оказываемся в группе, групповой фаворитизм способствует стабильности коллектива. Это наша внутренняя склонность оказывать предпочтение и содействовать тем, кого мы считаем членами своей группы. Также сообщают об эффекте Google (есть и другие поисковые системы!) — современная тенденция забывать информацию, которую, как мы знаем, точно найдем в интернете. Возможно, человеческий мозг эволюционирует, приспосабливаясь к технологиям вокруг, и позволяет компьютерам снять с себя некоторое напряжение!

Существует много других искажений — социальных, когнитивных, связанных с работой памяти, — которые появляются из-за особенностей работы нашего мозга, и мы вынуждены иметь с ними дело. Часто они действуют на подсознательном уровне, мы не знаем об их существовании. Однако выяснилось, что они оказывают огромное влияние на наше поведение и поведение всего общества.

Несовершенные компьютеры

Мы действуем не так, как компьютеры, — не всегда делаем все безупречно. Но важно понимать, что компьютеры тоже несовершенны, но в другом отношении. Они делают то, что написано в программе. Но если в программах есть дефекты, то компьютеры действуют неправильно. Хуже того, даже когда программы работают именно так, как задумал программист, действия компьютера все равно могут быть неверными — если у разработчика было неверное представление о желаемых результатах. И как мы видели, бывает, что в компьютеры заложены потенциальные ошибки. В редких случаях, если программа плохо продумана, оказывается, что компьютеры запрограммированы на неправильные действия. Из-за этого люди, которые ими пользуются, совершают ошибки. То есть компьютеры не просто должны осуществлять намерения — важно, чтобы эти намерения были верными.

Если верить в безупречность компьютерных программ, может случиться беда. Вопиющий пример — уголовное дело, которое в 2015 г. слушалось в британском суде. В больнице после инсульта умерли несколько пациентов, и двух медсестер обвинили в непреднамеренном убийстве. Полиция проверила журнал записей и обнаружила несоответствия в данных анализов крови, внесенных медсестрами и зафиксированных компьютером. Объяснение было очевидным: медсестры подделали записи, чтобы скрыть ошибки, которые привели к смерти пациентов. Но когда суд попросил эксперта по вычислительным системам проверить эти доказательства, выяснилось, что по самым разным причинам данные компьютера были ненадежны. Дело против медсестер развалилось. До этого момента полиция, администрация больницы и обвинители были абсолютно уверены, что компьютеры говорят правду, и в результате две невинные женщины могли попасть в тюрьму.

Понимать, как работают компьютеры и как они не работают, нужно не только тем, кто хочет стать программистом. Но программистам совершенно необходимо понимать людей. Только осознавая наши ограничения, предубеждения, особенности чувственного восприятия, они смогут писать программы, соответствующие поставленной цели, — программы, которые помогают людям, а не усложняют им жизнь (хотя бы отчасти).

Эффект рифмованности

В заключение давайте рассмотрим еще одно когнитивное искажение, которое достойно упоминания хотя бы потому, что оно очень странное — феномен Итона–Розена. Это искажение, которое часто называют эффектом рифмованности, подразумевает, что у нас есть тенденция признавать утверждение более точным или правдивым, если оно представлено в рифмованной форме. Этим трюком часто пользуются рекламисты. Точного объяснения этого феномена пока нет. Возможно, нам кажется, что рифмованное утверждение красиво и что оно создает приятный эстетический эффект.

Замечательная вещь — наш мозг. Он работает довольно причудливо и естественной склонности к вычислительному и логическому мышлению не проявляет (по крайней мере в некоторых случаях). Мы не думаем как компьютеры, хотя все идет к тому, что будет создаваться все больше компьютеров, которые будут думать как мы и, возможно, копировать некоторые наши странности. Только тогда они смогут воспринимать и ощущать мир так же, как мы.

Глава 13
Так что же такое вычислительное мышление?

Мы бегло ознакомились со многими примерами вычислительного мышления. Надеемся, у вас появилось общее представление о вычислительном мышлении и о том, как разные его элементы, такие как абстрагирование и алгоритмическое мышление, сочетаются и дают нам мощный инструмент решения задач и понимания мира. В этой, последней главе мы еще раз пройдемся по разным компонентам вычислительного мышления.

Вычислительное мышление

Вычислительное мышление — это свободный набор навыков для решения задач, который ориентирован преимущественно на создание алгоритмов. Они являются мощным инструментом, ибо после создания алгоритмы можно использовать для решения разных задач не задумываясь. Алгоритмы интересны специалистам по информатике, потому что они лежат в основе программ. Однако люди придумывали алгоритмы тысячелетиями, и началось это задолго до изобретения компьютера. Вычислительное мышление — навык не новый, но такое название он получил недавно.

В основе вычислительного мышления лежит алгоритмическое мышление, но помимо него используется ряд других методов, в числе которых абстрагирование, обобщение, декомпозиция и оценка. Также к его важным элементам относятся логическое мышление, сопоставление с образцом и выбор правильного представления данных для решения рассматриваемой задачи. Вычислительное мышление задействует научное мышление и благодаря таким подходам, как компьютерное моделирование, меняет современную науку. В основе вычислительного мышления лежит способность людей к глубокому проникновению в суть вещей, их сильные и слабые стороны. И прежде всего творческая деятельность.

Давайте рассмотрим по очереди все эти компоненты, многие из которых формируют основу для других областей и предметов и других подходов к решению задач.

Алгоритмическое мышление

Алгоритмическое мышление позволяет увидеть решение задачи в виде алгоритмов. Например, маршрут, который мы проложили, решая головоломку «Ход конем» и загадку экскурсовода, явился результатом серии инструкций, выполняя которые, нужно посетить все достопримечательности или все клетки на доске и вернуться к началу. Наше решение — простой алгоритм для экскурсии по городу и обхода доски. Можно использовать несколько маршрутов, при этом разные алгоритмы могут стать решением для одной задачи. Мы увидели, что фокусы — это тоже алгоритмы и фокусники используют их, чтобы создать магический эффект. Алгоритмы позволяют выигрывать в крестики-нолики и хорошо понимать пациентов с синдромом «запертого человека». Существуют алгоритмы приобретения знаний, которые в целом позволяют нам создавать разумные машины. При помощи алгоритмов зарабатывают деньги и создают произведения искусства. Более того, они спасают жизнь, будучи встроенными в медицинские приборы.

Почему, решив проблему, важно записать алгоритм? Во-первых, после этого ему можно следовать столько раз, сколько понадобится (снова и снова проводить экскурсии, всегда безошибочно играть в игру, каждый раз спасать жизнь...), и при этом не придется снова и снова решать одну и ту же задачу. Мы даже можем дать кому-то другому задание следовать алгоритму (например, младшему ассистенту, если вы менеджер туристического агентства; всем, кто посещает пациента с синдромом «запертого человека» в больнице; ассистенту фокусника...). В этом случае человеку не понадобится искать решение задачи с нуля. Сегодня алгоритмам следуют не только люди, как это было на протяжении тысячелетий. В эпоху компьютеров их превращают в программы, и на основе этих программ работу могут выполнять машины.

Компьютерное моделирование

Крайне важный элемент алгоритмического мышления — компьютерное моделирование.Можно взять из реального мира какое-то явление, которое хотите лучше понять, например погоду, и создать алгоритм, симулирующий это явление в виртуальном мире. Запустив этот алгоритм, вы будете прогнозировать погоду — например, пойдет ли завтра дождь. Если у вас есть хорошая компьютерная модель, то, симулируя различные процессы, вы будете в состоянии провести массу экспериментов. Это дает результаты гораздо быстрее, чем эксперименты в обычной жизни. А еще можно обработать модель математическими методами и сделать выводы о вероятных последствиях.

Компьютерное моделирование — главный способ, с помощью которого вычислительное мышление преобразует все остальные сферы. Например, существуют компьютерные модели работы мозга и функционирования экосистем. Биологи создают алгоритмические модели, например, сердца или раковых клеток и проводят виртуальные эксперименты. Кроме того, это позволяет меньше использовать подопытных животных, так как доступны виртуальные животные.

Экономисты создают компьютерные модели экономики, чтобы спрогнозировать, к каким потенциальным эффектам могут привести планируемые политиками изменения. Климатологи обращаются к моделям для прогнозирования возможных последствий глобального потепления. Компьютерные модели использовали и для того, чтобы понять природу творчества, например оценить, что отличает хорошую литературу и искусство.

К компьютерному моделированию прибегают в физике, биологии, химии, географии, археологии... и многих других областях. Оно позволяет найти новый подход к теме, какой бы она ни была. Кроме того, новаторы, создавая экономические отрасли будущего, обнаруживают новые ниши для бизнеса.

Компьютерное моделирование даже изменило мир компьютерных игр. Например, World of Warcraft — это просто компьютерные модели фантазийного мира, а спортивные игры — компьютерные модели занятий спортом. В обоих случаях в программы встроены модели физических законов, чтобы, например, все, что поднимается вверх, непременно опускалось вниз!

Расцвет компьютерного моделирования показал, что, чем бы вы ни занимались, крайне важно иметь навыки вычислительного мышления, а не просто уметь обращаться с компьютером и использовать информационные технологии.

Научное мышление

Для практикующих вычислительное мышление не менее важно и научное мышление. Чтобы поддержать научный процесс, скажем, компьютерным моделированием, надо знать, как правильно заниматься наукой. Например, нужно понимать, что результаты, полученные для модели, справедливы только для нее. Они рассказывают именно о конкретной модели, и если она не соответствует реальности, то не соответствуют и результаты. Все расчетные данные нужно проверять, выдвигая новые гипотезы и тестируя их. Но если вы не упускаете из виду этот момент, вычислительное мышление дает вам мощный инструмент для понимания мира. Научное мышление необходимо и в других отношениях — в частности, для оценки алгоритмических решений. Научные методы обеспечивают ряд способов, которые позволяют проверить, соответствуют ли цели наши алгоритмы. Мы еще вернемся к этому пункту.

Эвристика

Иногда действительно невозможно создать алгоритм, который обеспечит наилучшее решение для задачи — или вообще, или в доступное время (и это правда невозможно, а не просто трудно). В таких ситуациях используется эвристический алгоритм. Он не гарантирует оптимального решения, но обеспечивает разумный вариант в разумный срок. Для создания такого алгоритма необходимо эвристическое решение задачи. И пусть ответ не всегда будет лучшим — в большинстве случаев он окажется хорошим. По этому принципу действует ваш навигатор, когда прокладывает для вас путь.

Логическое мышление

Чтобы мыслить алгоритмически, необходимо логическое мышление, крайне тщательный и точный подход к деталям. Например, инструкции в алгоритме должны охватить все возможные варианты развития событий. Если в вашем алгоритме используется сложение, указали ли вы, что делать с отрицательными числами? Столкнувшись с ними, компьютер либо даст неправильный ответ, либо вообще зависнет. Разрабатывая алгоритм, нужно предельно логично оценить то, как он работает. Если не на бумаге, то уж точно в голове вам нужно иметь логические аргументы, подтверждающие его бесперебойную работу. Нельзя допустить, чтобы ваш спускаемый аппарат потерпел крушение, когда он наконец-то опустится на поверхность Марса спустя долгие месяцы, только потому, что вы забыли какую-то деталь. Как мы увидим далее, логическое мышление — это часть оценки.

Сопоставление с образцом

Умение видеть две одинаковые (или очень похожие) задачи — важный элемент вычислительного мышления, сопоставление с образцом. Мы все время занимаемся этим, даже не задумываясь, и специалисты постоянно используют в работе сопоставление с образцом — они узнают ситуацию и без колебаний делают то, что нужно. Этот же принцип лежит в основе многих программ: они сопоставляют правила с ситуацией и определяют, каким именно указаниям надо следовать. Программисты, создающие подобные программы, должны разработать образцы, на которые будет ориентироваться программа. Машинное самообучение тоже подразумевает сопоставление с образцом, но в этом случаи образцы подбирают сами программы.

При решении задач сопоставление с образцом помогает уменьшить объем работы, потому что при получении новой задачи позволяет не повторять одни и те же сложные операции каждый раз. Нужно найти аналогичную задачу из числа уже решенных и взять старое решение. Например, когда вы видите задачу или головоломку, связанную с составлением маршрута, нужно вспомнить о графах. Эту же мысль можно сформулировать по-другому: если вы видите, что задача соответствует модели передвижения из одной точки в другую, то для ее представления стоит использовать граф. Точки необязательно должны быть физически существующими местами. Например, это могут быть веб-страницы (с гиперссылками между ними), режимы будильника (с кнопочным переходом между ними), города (с перелетами из одного в другой) и так далее.

Представление

Решение проблемы можно облегчить, выбрав для нее хорошее представление, котороеявляется способом организации информации. Есть на удивление много возможностей представить одну и ту же информацию, и, как только вы это осознаете и с самого начала сосредоточитесь на выборе хорошего представления, задачи станут проще. Как мы видели на примере задач с составлением графа и игры «Бусы, хлеб, баня», хорошее представление значительно облегчает весь процесс как для людей, так и для компьютеров. Однако оно может полностью поменять используемый алгоритм. Порой очевидно, что благодаря верному представлению открываются возможности использовать простой и быстрый алгоритм вместо медленного и сложного. В этой книге мы ознакомились с разными представлениями — например, растровые изображения, состоящие из большого количества пикселов, формирующих решетку, и векторные изображения в виде линий и фигур. Мы узнали, что представление в виде сетки открывает самые разные возможности. Также мы увидели, что если числа хранятся в двоичном представлении на перфокартах, то возможен быстрый поиск и применение алгоритма упорядочивания. Представление образца в виде цифрового фильтра позволяет создать алгоритмы, помогающие компьютерам видеть. То есть выбор хорошего представления является важной частью абстрагирования и генерализации.

Абстрагирование

Абстрагирование — это сокрытие деталей разными способами с целью облегчить решение задачи. Есть масса разных способов, которые позволяют спрятать подробности. Этому способствует создание алгоритмов и их оценка.

Один из важных способов использования абстрагирования, который называется абстракция управления, мы рассмотрели на примере фокусов. Он состоит в объединении инструкций, что позволяет получить инструкции для достаточно больших этапов процесса. Идея здесь состоит в том, чтобы спрятать подробности отдельных маленьких шагов. В кулинарных книгах это встречается на каждом шагу. Там даются инструкции вроде «сварите картошку». Сюда входит много этапов: наполнить кастрюлю водой, включить конфорку, довести воду до кипения, положить картошку и так далее. Все эти шаги сведены вместе в одну простую команду «сварите картошку». Чтобы выполнить инструкцию, нужны все детали, но абстрагирование помогает записать инструкции и воспринимать алгоритм (или рецепт) в целом, чтобы работать с большими шагами. Изобилие подробностей мешает думать, пока вы не дойдете до них и не начнете с ними работать. Эта форма абстрагирования очень близка к декомпозиции, которую мы опишем ниже.

Есть еще один тип абстрагирования — абстрагирование данных. В этом случае прячут подробности хранения данных, то есть как они представлены на самом деле. Например, числа в реальности хранятся на компьютере в бинарном коде — как последовательность нолей и единиц. То есть число 16 выглядит как 00010000. Мы игнорируем этот факт, когда думаем о числах. У нас в голове именно 16 — десятичное число, которое мы привыкли использовать. Когда мы пишем программы, то используем в инструкциях десятичные числа, а не двоичные. Но наши программы просят пользователей вводить десятичные числа. При этом компьютер с ними не работает. Пользователям вообще не надо знать, что числа хранятся именно в таком виде, — эта подробность спрятана.

Мы используем абстрагирование не только при создании программ. Оно подходит и для их оценки. Например, как мы видели ранее, оно кстати при выборе алгоритма для помощи пациенту с синдромом «запертого человека». Если нужно решить, какой из двух алгоритмов с одинаковой задачей работает быстрее, не надо думать о времени как таковом. Отвлечемся от этих подробностей и будем думать только о выполненной работе — сколько операций нужно провести, чтобы довести до конца каждый алгоритм и справиться с задачей. Если для одного алгоритма нужно выполнить 100 инструкций, а для другого — только 10, то второй будет быстрее. Проверяем это, просто пересчитывая операции, не засекая время. Мы прячем подробности о временны`х затратах на операции, чтобы облегчить себе задачу.

Обобщение

Идея взять решенную проблему и приспособить ее решение (алгоритм) к другим подобным задачам называется обобщением. Предположим, что нужно найти свое имя в списке рассадки гостей. Этот список — представление имен, из которого мы узнаем, где сидим. Вместо того чтобы искать в случайном порядке, мы начинаем сверху и проверяем каждое имя по очереди, пока мы не дойдем до своего. Другой пример — надо найти на полке CD, и мы понимаем, что это похожая задача. Таким образом мы осуществляем сопоставление с образцом — сравниваем одну задачу с другой. Как только мы осознаем, что две задачи сводятся к одной, то используем для обеих одно и то же решение, и необходимость поиска нового алгоритм отпадает. Мы начинаем с одного конца и ведем пальцем по полке, проверяя каждый диск по очереди, пока не найдем нужный (или не доберемся до конца, что будет означать отсутствие диска). Мы обобщили и преобразили алгоритм (решение для первой задачи) и используем его для решения новой задачи.

Мы можем пойти еще дальше, если осознаем, что каждый раз, когда у нас есть каким-то образом выстроенная последовательность и необходимо что-то найти, можно использовать это решение. Итак, мы обобщили задачу поиска имен до задачи поиска чего угодно и обобщили список имен до любой выстроенной последовательности вещей. Мы преобразили наш алгоритм в общий алгоритм поиска. Теперь он подходит не только для конкретной задачи, но для любой задачи такого рода. Его можно использовать каждый раз, как только понадобится что-нибудь найти. Мы обобщили решение, которое было изобретено для решения всего одной задачи (найти наше имя), но оно подошло для целого класса проблем.

Обратите внимание: чтобы провести обобщение, необходимо скрыть часть деталей. Нам не нужно думать об особенностях имен или дисков, поэтому мы обобщили их до «элемента». Мы используем абстрагирование, чтобы провести обобщение.

Иногда мы проводим обобщение, чтобы создать очень общие алгоритмы, которые можно использовать во многих ситуациях, как показано выше. В других случаях мы понимаем, что новая задача в совершенно иной области похожа на уже решенную нами, и поэтому мы делаем однократное обобщение — переносим задачу (а значит, и решение). Например, в телефонах используется функция предиктивного набора текста. Когда вы начинаете вводить слово, телефон догадывается по набранным буквам, что за слово вы набираете. Парализованные люди, которые не могут говорить, общаются, выбирая буквы по системе моргания. Тот же самый алгоритм предиктивного набора текста можно использовать и в этой ситуации. Люди точно так же могут догадаться, что им хотят сказать, по первым буквам. Один алгоритм можно использовать для двух разных с виду проблем, как только становится очевидным их сходство при сопоставлении с образцом.

Сопоставление с образцом и обобщение используют на самых разных уровнях — от осознания, что задача аналогична уже решенной, и до понимания, что небольшие фрагменты задач одинаковы. Часто при написании программы видно, что отдельные ее части похожи на то, с чем мы уже имели дело. Предположим, нам нужно, чтобы программа каждый раз спрашивала, хотим ли мы сделать что-то еще раз (например, сыграть в игру снова после выигрыша). Если мы уже писали код для такого случая, то имеет смысл адаптировать его и интегрировать в новую программу, не продумывая необходимые команды с самого начала.

Обобщение помогает и при оценке. Предположим, что мы создали некий общий алгоритм. Его оценивают один раз, и все, что при этом узнают о нем, применимо к каждому новому случаю использования. Например, сведения об абсолютной скорости работы алгоритма и скорости его работы по сравнению с другими алгоритмами являются основанием для решения, подходит ли он для каких-либо новых задач.

Декомпозиция

Разделение крупной задачи на мелкие части, с которыми легче справиться, называется декомпозицией. Мы видели применение этого принципа, когда делали робота-мошенника и собрали целое, продумав все отдельные компоненты. Это очень действенный способ решения проблем. Именно декомпозиция позволяет писать сложные программы, состоящие из миллиона инструкций. Без нее у нас не было бы программ, позволяющих делать все то, для чего сейчас используются компьютеры.

Использование метода декомпозиции при написании программ тесно связано с абстракцией управления. Идея состоит в том, чтобы разбить программу на массу более мелких задач. Каждую из этих небольших программ написать легко. После этого становится легче написать большую объединяющую их программу, потому что не надо думать обо всех деталях. Как только части завершены, мы учитываем только то, что они делают, а не как они это делают. Чтобы облегчить процесс, каждой части присваивается имя, которое четко указывает, чтó она делает, но подробности при этом скрыты (такого рода наименования — это еще один вид абстракции). Потом при объединении маленьких программ уже не надо думать о мелких деталях.

Таким образом, декомпозиция обеспечивает еще один способ использования обобщения. Если небольшие программы написаны в достаточно общем ключе, то их используют в других больших программах. Возможно, для решения определенных подзадач пригодятся уже существующие программы, если при сопоставлении с образцом выявится необходимое соответствие. Кроме того, существуют особые приемы, позволяющие использовать декомпозицию для быстрого нахождения работающих решений. Один из вариантов — алгоритм «разделяй и властвуй». Идея заключается в том, чтобы решить задачу, найдя способ разделить ее на более мелкие, но в остальном одинаковые задачи. Чтобы решить проблему поиска по телефонному справочнику, мы можем открыть его в середине и посмотреть, находятся ли напечатанные там фамилии до или после нужной нам фамилии. После этого мы игнорируем одну из половин, так как знаем, где надо искать. У нас остается похожая, но менее масштабная проблема — поиск в половине телефонного справочника. Мы решаем эту задачу так же — открываем выбранную часть на середине и так далее, пока не найдем нужную фамилию. Это позволяет решить задачу гораздо быстрее. Такой подход — пример решения задачи с использованием рекурсии, особого вида алгоритмического мышления. На этой идее основан подход к созданию алгоритмов, в основе которого лежит деление задачи на похожие, но меньшего объема. Метод «разделяй и властвуй» выделяется в том плане, что задачу делят пополам (или на трети, четверти и т.п.), чтобы получившиеся при этом задачи были примерно одного объема, но гораздо меньшего по сравнению с общей задачей и, следовательно, легче в решении, чем изначальная.

Понимание людей

Высокие технологии в конечном итоге создаются для людей и в помощь людям. Это значит, что вычислительное мышление главным образом связано с решением проблем людей, а не технологий. Поэтому алгоритмическое мышление должно включать понимание людей и особенно их сильных и слабых сторон. Мы видели это на многочисленных примерах — от помощи пациентам с синдромом «запертого человека» до заботы о том, чтобы медсестры не делали ошибок. Вот еще один пример, подтверждающий эту мысль. Представьте, что вы пишете алгоритм, обеспечивающий безопасность банковских операций в интернете. Можно придумать алгоритм, который потребует пароля из 1000 произвольных символов, куда нельзя вставлять существующие слова. Это, безусловно, обеспечит высокую степень безопасности! А еще это будет очень глупо. Ни один человек, за исключением пары случайных гениев, не запомнит такой пароль. Алгоритм окажется бесполезным. Решение задач с помощью вычислительного мышления должно быть связано с пониманием возможностей людей.

Оценка

Как только алгоритм написан, его важно оценить. Необходимо проверить, работает ли он. В частности, надо подтвердить, что алгоритм удовлетворяет ряду требований, описывающих задачу.

Оценка подразумевает проверку соответствия вашего решения поставленной цели и его оценку по нескольким параметрам. Самый главный из них — функциональная корректность. Действительно ли ваш алгоритм работает? Это необходимо проверять всегда! Что бы ни случилось, он должен непременно давать правильный ответ. Обязательно в этом убедитесь. В противном случае человек или машина, которые будут его использовать, могут оказаться в сложной ситуации, слепо выполняя неправильные действия, и в итоге не будут знать, что делать. Мы видели это, в частности, на примере с фокусом, где надо было угадывать выбранные предметы. Даже если мы предусмотрим все возможные варианты, ничего не получится, если кто-нибудь выберет один из наших секретных предметов. Ни фокусники, ни компьютеры не должны оставаться без плана действий в подобных случаях.

Еще можно оценить производительность в плане скорости. Насколько быстро работает ваш алгоритм? Есть ли другие, которые справятся с задачей быстрее? Есть ли конкретные ситуации, когда алгоритм будет работать медленно? Насколько важны эти ситуации? Например, алгоритм быстрой сортировки quicksort обычно работает очень быстро. Однако, если одной из его версий заказать сортировку уже отсортированных позиций, работа будет идти до абсурдного медленно. То есть процесс сортировки уже расположенных по порядку позиций займет больше времени, чем сортировка бессистемно собранных позиций. Это отличный алгоритм, но было бы глупо использовать его, если вы знаете, что у вас почти все расположено по порядку. Ситуация, когда подходит один-единственный алгоритм, встречается редко. И нужно обязательно проверить, насколько он подходит для конкретного случая.

Третья, очень важная часть оценки — проверка соответствия разработанного решения поставленной цели. Как мы говорили, алгоритмы существуют для людей. Они должны работать так, чтобы мы могли их использовать, что уже обсуждалось при рассмотрении алгоритмического дизайна. Следовательно, вам необходимо оценить, насколько легко пользоваться программами, системами и решениями и какие впечатления останутся у пользователей. Вы же не хотите, чтобы у пользователей получались ошибочные результаты, они разочаровывались и злились? В ходе оценки вы, по сути, задаете вопрос: «Хорошо ли это работает, если учесть особенности людей? Учтены ли в разработанном решении наши сильные стороны и ограничены ли проблемы, связанные со слабыми сторонами?»

Предположим, вы разрабатываете медицинский прибор, который будет вводить пациентам обезболивающее. Медсестра настраивает дозу, включает подачу, и прибор в течение нескольких часов проводит внутривенное вливание лекарства. Конечно же, вам нужна функциональная корректность. Если по рецепту необходимо вводить 15,5 мг в час в течение шести часов и медсестра это запрограммировала, то прибор должен точно выполнять задачу. Кроме того, он должен работать быстро. Если медсестре придется ждать начала работы несколько минут после введения значений дозы, так дело не пойдет. Что еще важнее, он должен быть легким в использовании, уметь предотвращать ошибки и ликвидировать последствия. Если медсестра по ошибке вводит 155 мг вместо 15,5, что является опасным объемом, то аппарат должен по крайней мере предупредить медсестру и дать возможность исправить ошибку. Еще лучше, если он будет сконструирован так, чтобы вероятность таких ошибок изначально снижалась.

При оценке используются самые разные приемы и навыки. Прежде всего подразумевается строгое тестирование — очень хорошо организованная проверка алгоритма или программы в действии, которая позволяет понять, работает ли она вообще. Это предполагает проведение большого количества тестов, а не одного-двух. Кроме того, для тестирования надо выбирать хорошо продуманные ситуации, чтобы избежать сюрпризов в будущем. Для этого требуется логическое мышление, с помощью которого будет легче определить, что необходимо проверить для полного учета всех возможностей.

Существует еще и комплементарный подход к тестированию, который сводится к строгому аргументу. Вместо того чтобы запустить программу и смотреть, работает ли она, можно использовать право на аргумент. Для этого нужно с помощью логических рассуждений доказать, почему определенные тесты гарантируют, что система работает правильно. Крайнее проявление этого метода — использование только логических доказательств, являющихся разновидностью математических доказательств. Когда вы создаете алгоритм или программу, вы представляете себе причины, в соответствии с которыми, с вашей точки зрения, они должны работать. На стадии оценки вы проверяете эти причины и смотрите, не пропустили ли вы какие-то детали. Часто такие доказательства делаются при абстракции системы. Это означает, что неважные детали игнорируются, что облегчает поиски доказательства. Однако необходимо различать, когда результаты тестирования применимы к модели системы, а когда — к самой системе. Если модель правильная, это не всегда значит, что правильна и система.

Кроме того, можно оценивать части решения по отдельности. При этом используется метод декомпозиции, а проблема или система рассматривается как набор более простых элементов, с которыми работают отдельно. Поскольку части меньше самой системы, то и делать это проще. Оценка не всегда проводится, когда решение готово, — ее нужно делать и в процессе разработки решения, алгоритмов, программ и их интерфейсов. Если вы работаете над решением и создаете первые прототипы, их надо оценивать в процессе создания с разных сторон и по ходу дела решать возникающие проблемы. Здесь реально помогает декомпозиция, так как позволяет оценить каждую малую часть индивидуально сразу же по завершении. С ее помощью проверяют, работает ли каждый элемент, и исправляют ошибки еще до того, как придется думать о том, работает ли программа в целом.

Когда дело доходит до оценки соответствия решений целевому назначению, используют методы, немного похожие на тестирование, — методы наблюдения. Разница здесь в том, что для такого рода оценки нужны обычные пользователи оцениваемой системы. Эксперимент можно провести в лабораторных условиях — в сущности, это будет научный эксперимент. Другой способ — «выйти в поле» и посмотреть, как систему используют в обычной жизни. В обоих случаях мы смотрим, не пойдет ли что-нибудь не так, не столкнутся ли люди с какими-то трудностями, и все время задаем себе вопрос, можно ли изменить систему, чтобы людям стало проще с ней работать.

И опять мы используем аналитические методы и логические рассуждения. В принципе, для этого нужно привлечь специалистов, которые хорошо знают особенности людей, понимают, что делает дизайн плохим или хорошим, и могут организованно оценить системы. Их цель — предсказать потенциальные проблемы, то есть те особенности, которые могут привести к трудностям. Например, эксперты могут взять какую-то задачу и на каждом этапе спросить: «Может ли человек неправильно понять, что здесь нужно делать и как?» Эксперты используют особые принципы, например: «В случае ошибки необходимо, чтобы всегда можно было отменить последний шаг». Если они обнаруживают ситуацию, где такая отмена невозможна, то сообщают об этом как о проблеме, требующей решения.

Креативность

Создание алгоритмов — процесс творческий, и поэтому с ним тесно связан навыккреативности. Конечно же, можно продвигаться очень медленно и использовать хорошо известные приемы — так начинает большинство. Однако блестящие программисты придумывают совершенно новые алгоритмы либо для старых, либо для совершенно новых задач. Они видят возможности там, где никто их не заметил. Идеи по реализации этих концептов, конечно же, тоже требуют творческого подхода. Другие элементы вычислительного мышления также связаны с креативностью. При абстрагировании креативность помогает выделить частности, которые лучше скрыть, чтобы значительно облегчить задачу. Подобным образом для обобщения и сопоставления с образцом порой нужны творческие озарения, которые позволяют увидеть связь между совершенно разными с виду ситуациями. Как оценить, насколько легко пользоваться мобильным приложением в реальных ситуациях? В лаборатории можно проследить за всем, что делают пользователи. Вне стен лаборатории это нереально... или реально?

Один предприимчивый специалист, столкнувшись с этой проблемой на раннем этапе развития подобных технологий, придумал для участников эксперимента специальный головной убор с камерами. С его помощью наблюдали, что делают участники и что происходит вокруг.

Для креативности нужны подходящие условия. Участники должны быть склонны к игре и к ситуациям, которые ей способствуют. Помогает, если человеку хочется заниматься интересными вещами, ведь информатика — очень интересное занятие. Вам понадобятся время и место, которые позволят отпустить мысли на свободу. Кроме того, необходимо отсутствие стресса и жестких сроков. Конечно, самые творческие идеи приходят не индивидам, а группам, в которых принято обмениваться идеями и подпитываться креативностью друг от друга. Компании (и страны), которые содействуют такой организации труда, действительно изменят мир! Неудивительно, что IT-компании из числа самых больших и успешных действуют именно так.

Дело в том, что креативность необходима не только при создании алгоритма. Иногда она нужна, чтобы предложить задачу для решения. Необходимо найти такую идею, чтобы с появлением алгоритмов для ее реализации произошли настоящие изменения. Придумать алгоритм, не похожий ни на что известное, — способ полностью преобразить задачу, а значит, и наш образ жизни. Это получается особенно хорошо, если ваших творческих способностей хватило, чтобы найти задачу, которую никто никогда не замечал, и решить ее. Из креативности рождаются инновации, и для их внедрения нужны люди, у которых есть энергия и навыки, чтобы довести идею до конца. Все крупные инновации, связанные с компьютерами, такие как Всемирная сеть, социальные сети, интернет-магазины и так далее, изначально появились благодаря людям с творческими способностями, а затем, чтобы эти инновации стали обыденной реальностью, к их разработке подключили специалистов с разными навыками, в том числе и деловыми.

Резюме

К вычислительному мышлению относится много навыков. И важно понимать, что они не применяются по отдельности, но взаимосвязаны и дополняют друг друга в процессе решения задач. Многие из этих навыков пересекаются с навыками математиков, дизайнеров, ученых, инженеров, а также писателей, историков и многих других. Вычислительное мышление, используемое в информатике, — это набор умений, который приобретается в ходе этого объединяющего и взаимообогащающего процесса, что позволяет по-новому взглянуть как на задачи, так и на системы. В конечном итоге программисты при разработке решений с использованием вычислительной техники берут эти навыки за основу. Превращая алгоритмы в программы, вычислительное мышление изменило образ нашей жизни, работы и отдыха, и перемены продолжаются.

Вычислительное мышление не является мышлением компьютеров. Это образ мыслей, который люди используют, чтобы добиться от компьютеров удивительных результатов. Но поскольку с каждым годом появляются все более мощные системы искусственного интеллекта, мы все больше программируем сами машины на использование вычислительного мышления.

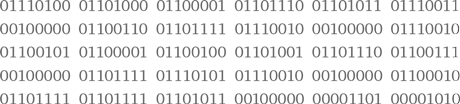
Дополнительная литература

Мы читаем о математике, фокусах и информатике примерно 40 лет. В этом списке приведены некоторые наши работы и другие ресурсы, которые вдохновляли нас во время создания этой книги.

Это информатика?

Информатика повсюду вокруг нас, стоит только приглядеться, — и не только в компьютерах.

Computer Science for Fun — www.cs4fn.org. Тысячи статей обо всех аспектах занимательной информатики, а еще журналы и буклеты.

CS Unplugged — csunplugged.org/. Место для информатики без применения компьютеров, где можно скачать книгу с классными занятиями.

Curzon P. Computing Without Computers. v0.15, Feb 2014. Ссылка для скачивания: teachinglondoncomputing.org/resources/inspiring-computing-stories/computingwithoutcomputers/.

Curzon P. Computational Thinking: HexaHexaflexagon Automata. Queen Mary University of London, 2015. Гексафлексагоны стали способом исследовать конечные автоматы.

Teaching London Computing — www.TeachingLondonComputing.org. Ресурс для учителей, помогающий обучать междисциплинарным навыкам вычислительного мышления. Есть дополнительные материалы по многим темам, освещенным в этой книге.

Левитин А., Левитина М. Алгоритмические головоломки. — М: Лаборатория знаний, 2017. Больше алгоритмических головоломок, чем можно себе представить, которые используются как подспорье в разработке алгоритмов.

Маккормик Дж. Девять алгоритмов, которые изменили будущее. — М: ДМК Пресс, 2014. Подробное исследование важных алгоритмов, которые изменили нашу повсе­днев­ную жизнь.

Хофштадтер Д. Р. Гедель, Эшер, Бах. Эта бесконечная гирлянда. — Самара: Бахрах-М, 2001. Превосходная книга в духе Льюиса Кэрролла, получившая Пулитцеровскую премию, об интеллекте, машинах, информатике, доказательствах, шаблонах, силе правил и многом другом.

Это математика?

Многие книги вроде бы о математических развлечениях на самом деле полны игр, головоломок и любопытных фактов из области информатики. Вот некоторые из числа наших любимых.

Berlekamp E., Conway J., Guy R. Winning ways for your mathematical plays. Academic Press, 1982. В книге анализируется масса игр и головоломок. Также дается подробный обзор игры «Жизнь» от авторов этой игры.

Eastaway R., Wyndham J. How long is a piece of string. Robson Books, 2003. Фракталы, задачи об упаковке багажа и доказательства.

Eastaway R., Wyndham J. Why do buses come in threes? Robson Books, 1998. Графы, неформальная логика и магия.

Stewart I. The magical maze. Phoenix, 1998. Представление в виде графов, исследование лабиринтов, фокусы и многое другое.

The Puzzler — www.puzzler.com. Мы решаем очень много головоломок из разных источников, но указываем именно The Puzzler, потому что он просто чудесен.

Гарднер М. Нескучная математика. Калейдоскоп головоломок. — М: АСТ, Астрель, Аванта+, 2008. Молниеносные вычисления, тасовка карт и игра, на которой основана игра «Бусы, хлеб, баня».

Гарднер М. Лучшие математические игры и головоломки, или Самый настоящий математический цирк. — М: ACT, Астрель, 2009. Могут ли машины думать, булева алгебра, ряды Фибоначчи и оптические иллюзии.

Кордемский Б. Математическая смекалка. — М.: Альпина Паблишер, 2017. Очень-очень много алгоритмических и иных головоломок.

Математические головоломки и развлечения. — М: Мир, 1971. Гексафлексагоны, беспроигрышная игра в них и крестики-нолики, карточные фокусы, лабиринты, механические головоломки, самообучающиеся машины, «солитер» и многое другое.

Это магия?

О фокусах написано очень много книг. Вот некоторые из тех, что вдохновляли нас.

Bobo J. B. Modern Coin Magic. Dover, 1982. Содержит алгоритмические фокусы с монетами.

Diaconis P., Graham R. Magical Mathematics. Princeton University Press, 2013.

Fulves K. Self-Working Card Tricks. Dover, 1976. Целая книга алгоритмических карточных фокусов.

Klein G. Sources of Power. MIT Press, 1999. Как специалисты делают свое дело. Автор предполагает, что интуиция — на самом деле сопоставление с образцом.

Nelms H. Magic and Showmanship. Dover, 1969. Более общее описание навыков, необходимых фокуснику.

Это что-то другое?

Норман Д. Дизайн привычных вещей. — М.: Вильямс, 2006. Узнайте у привычных вещей о дизайне и практичности, и вы поймете, как это применимо и к виртуальному миру.

Боби Ж.-Д. Cкафандр и бабочка. — М.: Рипол-Классик, 2009. Поразительная книга о любви к жизни, написанная автором с синдромом «запертого человека».

По мотивам...

Главы этой книги — переработанные тексты для наших ресурсов cs4fn, Teaching London и других. Также в число оригинальных текстов входят:

Curzon P. Computational thinking: searching to speak. Queen Mary University of London, 2013. Сжатый ранний вариант главы 2 о синдроме «запертого человека».

Curzon P. Cut Hive Puzzles. Queen Mary University of London, 2015. Более сжатая ранняя версия главы 4, в которой рассказывается о головоломке «Соты».

Curzon P. Computational thinking: Puzzling tours. Queen Mary Uni­versity of London, 2015. Сжатый ранний вариант главы 5 о графах.

McOwan P. W. Mini-megalomaniac AI is already all around us, but it won't get further without our help. The Conversation, 2 июня 2015 г. URL: theconversation.com/mini-megalomaniac-ai-is-already-allaround-us-but-itwont-get-further-without-our-help-42672.

Оглавление

Предисловие

Об авторах

Благодарности

Глава 1 Мышление будущего

  Что с ним делать?

  Навыки для XXI века

  Алгоритмическое мышление

  Изменить мир

  Научное мышление

  Вычислительное мышление

Глава 2 В поисках способа говорить

  Сидром «запертого человека»

  Просто как A, B, C

  Как это сделал Боби?

  Проверяем детали

  Улучшаем метод

  Насколько это быстро?

  20 вопросов?

  Насколько это эффективно?

  Новый алгоритм

  Коды для букв

  Выбираем лучшее решение

  Делаем жизнь Боби лучше

  Главное — алгоритмическое мышление

  Еще важнее — понять человека

  Ему подошло

Глава 3 Магия и алгоритмы

  «Сон об австралийском маге»

  Хитрые алгоритмы

  Придумываем фокусы

  Делим на части

  Всегда ли получается фокус?

  Перфокарты

  Две системы

  Двоичные перфокарты

  Как же это работает?

  И снова изобретаем фокусы

  Новые фокусы с помощью информатики

Глава 4 Головоломки, логика и образцы

  Головоломки «Улей»

  Выводим правила

  Другие головоломки

  Логическое мышление и опыт

Глава 5 Головоломные маршруты

  Две задачи

  Одно решение на двоих

  Мосты Кенигсберга

  Собираемся и путешествуем

Глава 6 Создание бота. Руководство для начинающих

  У роботов своя история

  Как создать «разум» для робота

  Создаем своего виртуального собеседника

  Понимает ли вас виртуальный собеседник?

Глава 7 Создаем мозг

  Создаем обучающийся мозг

  Играем в «Снап!» с нейронной сетью

Глава 8 Делаем робота-мошенника

  Разум-предсказатель

  Этика и мировое господство

Глава 9 Сетки, графика и игры

  Решетки и игры как изображения

  Жизнь как игра

  Игры, в которые играют люди

Глава 10 Видим за деревьями лес

  Магия чтения мыслей

  Простая магия

  Увидеть мир таким, какой он есть

Глава 11 Медицинские чудеса на просвет

  Срез жизни

  Сыграем в морской бой

  Вернемся к рентгеновским лучам

  Еще больше измерений

Глава 12 Компьютеры и мозг

  Думаем как компьютер?

  Игра с несовпадением. Невозможное ограбление

  Мир иллюзий

  Математическая модель сознания

  Предубеждения мозга

Глава 13 Так что же такое вычислительное мышление?

  Вычислительное мышление

  Алгоритмическое мышление

  Компьютерное моделирование

  Научное мышление

  Эвристика

  Логическое мышление

  Сопоставление с образцом

  Представление

  Абстрагирование

  Обобщение

  Декомпозиция

  Понимание людей

  Оценка

  Креативность

  Резюме

Дополнительная литература