Геометрия скорби. Размышления о математике, об утрате близких и о жизни (fb2)

- Геометрия скорби. Размышления о математике, об утрате близких и о жизни (пер. Ольга Александровна Акимова) 4376K скачать: (fb2) - (epub) - (mobi) - Майкл Фрейм

Майкл Фрейм
Геометрия скорби. Размышления о математике, об утрате близких и о жизни

Michael Frame

Geometry of Grief

Reflections on Mathematics, Loss, and Life

The University of Chicago Press

Издательство выражает благодарность Вадиму Шурыгину и Эдуарду Лернеру за помощь в подготовке настоящего издания.

Licensed by The University of Chicago Press, Chicago, Illinois, U.S.A.

Пролог

Папа, это так страшно.

– Видишь самую яркую звездочку на небе?

– За деревом, посредине? Вон ту, Рути?

– Точно. Это Венера. Планета, огромный мир, почти как наша Земля. Она всегда окутана облаками. Никто еще не видел поверхности Венеры.

– Если там всегда облачно, значит, на Венере холодно.

– Не обязательно. Венера ближе к Солнцу, чем Земля. Возможно, облака удерживают тепло, и там очень жарко.

– Понятно. Сегодня небо ясное, так что нам прохладнее, чем в пасмурную погоду.

– Верно, Майки. Ну что, пойдем в дом?

– А другие планеты видно на небе?

– Сегодня не видно.

– А можно нам еще немного посмотреть на светлячков?

– Конечно.

Это был один из вечеров на исходе лета 1958 года. В багрянце неба, плавно переходящем в густо-синий, проглядывали редкие звезды, и среди них выделялась яркой точкой Венера. Мы ужинали вместе с моей бабушкой и тетей Рути, папиной сестрой, в их доме в Саут-Чарлстоне, штат Западная Виргиния. Мне было семь, моей сестре Линде – четыре, а брату Стиву – два. На задний двор вышли только мы с Рути. Остальные, как это называла мама, «вели светскую беседу» на крыльце. Мы жили в Сент-Олбансе, в каких-то восьми милях отсюда, и часто навещали бабушку и тетю Рути. Я не понимал, зачем взрослым вести светские беседы. Что там можно обсуждать? Они просто сплетничали о соседях и родственниках.

Мы с Рути были не такими. В тот день после полудня мы сидели в огороде и завороженно наблюдали за целеустремленным движением муравьев и беспорядочными прыжками кузнечиков. Пытаясь объяснить их поведение, я выдумывал замысловатые истории из мира природы; Рути предлагала гораздо более простые альтернативы моим рассказам. Она никогда не упоминала «бритву Оккама», но именно Рути впервые показала мне красоту простых решений. А также действенность принципа экономии: машина Голдберга – сложный агрегат, занимающий целую комнату и выполняющий какую-нибудь простую задачу вроде разбивания яйца, – слишком хитроумно устроена и часто допускает ошибки. Мои запутанные измышления, вероятно, были неплохим упражнением для ума, но неужели я думал, будто природа настолько глупа? Многие годы спустя я понял, что именно Рути наставила меня на путь науки. Любопытство, как она считала, – важнейшее свойство разума, а детское любопытство, толкающее на логические ухищрения маленького человека, который только открывает для себя этот огромный мир в его разнообразных аспектах и динамике, и есть самое прекрасное, что может увидеть взрослый. Родители, бабушки, дедушки, другие дяди и тети тоже поощряли мое любопытство, но Рути по-настоящему взращивала его, добавляя толику скептицизма, и всегда подыскивала какую-нибудь книгу по интересующей меня теме. Именно Рути вывела меня на тот путь, что спустя шестьдесят лет приведет к написанию этой истории.

Когда в начальной школе меня спрашивали, кем я хочу быть, то, в отличие от своих одноклассников, желавших стать полицейскими, пожарными или лесничими (профессии астронавта в ту пору еще не существовало – да, я такой старый), я говорил, что стану физиком, математиком или астрономом. На самом деле, в этом возрасте каждый ребенок – натуралист. Летним утром окрестные леса таили бездну удивительных открытий. Мое детское воодушевление не знало границ. Хотя родители были небогаты, их финансов хватало на детские творческие исследования. Чтобы измерять мощность термопары (это медный и стальной провода, скрученные вместе и преобразующие тепло в слабый электрический ток), отец моего одноклассника купил дорогой вольтамперметр. Я сделал гальванометр: две намагниченные иглы, воткнутые в прямоугольник из картона, подвешенный на нитке внутри проволочного кольца. Кто из нас радовался больше, когда его прибор показывал слабый ток?

Рути не помогала мне придумывать опыты – это делал папа, он разрешил мне устроить небольшую лабораторию в углу своей мастерской, – но именно Рути помогла мне осознать, что я могу ставить опыты и сам находить ответы на некоторые из своих вопросов.

Незадолго до моего одиннадцатилетия Рути заболела. У нее обнаружили лимфому Ходжкина – болезнь, излечимую в наши дни, но не в начале 1960-х. Ей прописали химиотерапию, кажется, мустаргеном, но она лишь промучилась на несколько месяцев дольше и умерла, когда мне не исполнилось и двенадцати. Я навещал Рути во время болезни, но почти ничем не мог ей помочь. Я стоял у ее кровати, положив свою маленькую ладонь на предплечье Рути, и пытался разговаривать с ней. И никак не мог найти нужные слова. После этих посещений, уже дома, мама обнимала меня и гладила по голове. Я понимал, что должен был больше разговаривать с Рути. Она столько сделала для меня, и сейчас я должен был отплатить ей тем же. Рути нуждалась в том, чтобы я говорил с ней, ведь я был ее любимчиком. Впоследствии я понял, что мама пыталась справиться с собственным горем. Она знала положение вещей гораздо лучше, чем я, она знала, что болезнь победит, а Рути проиграет это сражение. Папа сам заговорил со мной о болезни своей сестры. Он прямо так и сказал: Рути скоро умрет. Я был благодарен ему за честность. В том, что Рути уйдет или, что еще хуже, отправится к ангелам на небеса^[1]^[2], не было ничего сверхъестественного. Ее жизнь должна закончиться, и совсем скоро.

– Это несправедливо. У нас с Рути еще столько дел впереди. Она обещала, что мы купим телескоп, будем смотреть на планеты. Я уже полгода откладываю карманные деньги. Это просто несправедливо.

– Сынок, жизнь несправедлива. Рути заболела не потому, что сделала что-то плохое. Она просто заболела. Иногда случается что-то хорошее, иногда – что-то плохое. Мы можем лишь постараться делать так, чтобы случалось больше хорошего и меньше плохого. Но происходящее очень часто от нас никак не зависит.

– Папа, это так страшно.

– Да, сын, страшно.

Той ночью я придумал план. Я буду много, много трудиться. Только учеба – никаких больше пряток-догонялок или глупых сказок для малышей. Я досрочно закончу школу, поступлю в колледж, потом в магистратуру, отучусь на медицинском факультете, стану ученым, найду лекарство от лимфомы Ходжкина, дам его Рути и спасу ее. В одной из версий моей фантазии я летел на вертолете из своей научной лаборатории в больницу к Рути. Мне страшно нравился придуманный план. Я расписал его маме и сказал, что попрошу Рути не волноваться и спасу ее. Я думал, мама обрадуется, но она очень расстроилась и сказала, что мне нельзя говорить об этом Рути.

– Но почему? Ты не хочешь, чтобы она знала, что всё будет хорошо?

– Майки, я не хочу, чтобы ты будил в ней надежду, – ложь, но приятная, сладкая ложь. – Как бы ты ни старался, ты не сможешь спасти Рути.

Умом я понял, что мама права. Я пошел в городскую библиотеку, нашел книгу по онкологии (до этого я спросил у мамы, как называется наука, изучающая рак) и отыскал в ней показатели выживаемости при лимфоме Ходжкина. Цифры оказались неутешительными. Но я не мог представить себе мир без Рути. Ведь впереди у нас были долгие годы, полные научных открытий. Да и как могла Рути оставить свою дорогую маму, Луверну Фрейм, добрейшую и милейшую из всех взрослых, которых я знал? Существует же какой-нибудь выход, и я обязательно его найду.

Но Рути скончалась. Папа был с ней в больнице и держал ее за руку, пока она умирала. Когда он вернулся домой, я всё прочел по его лицу. Он рассказал об этом маме, Линде и Стиву. Они заплакали, а я нет. Наконец мама сказала, что Рути была смертельно больна, что она не могла поправиться и что, к счастью, она уже отмучилась.

– Рути мучилась? – простонала Линда.

А потом они со Стивом начали бегать кругами с дикими воплями. Наконец они успокоились, продолжая тихо всхлипывать. Я и раньше знал, что Рути мучилась. Ожидая в больничном коридоре за дверью ее палаты, пока папа спросит, можно ли мне войти, я иногда слышал ее стоны. Она страдала, а теперь – нет. Неужели покой небытия лучше, чем почти непрекращающаяся боль? Неразрешимый вопрос для двенадцатилетнего человека. Неразрешимый и сейчас…

Папа не захотел, чтобы мы, дети, пошли на похороны. Мама с папой поехали туда, а мы остались с мамиными родителями, Берлом и Лидией Эрроувуд. В дедушкиной мастерской я нашел мешок с воздушными шариками. Дедушка был ювелиром и ремонтировал разные часы. Для изготовления некоторых сплавов дедушка пользовался газовой горелкой, поэтому в мастерской стоял баллон с газом. Я наполнил шарик газом, завязал его, вышел во двор перед домом, подальше от деревьев и выпустил свой шар в небо. Это был печальный символический жест: он являл собой все те опыты, которые мы планировали провести с Рути и которые теперь навсегда остались неосуществленными. Словно закрылась некая дверь.

И сам я закрылся от мира. Я уже ничем не мог помочь Рути, но, возможно, в будущем принесу пользу другим людям. Я весь ушел в книги и научные исследования. Родители уговаривали меня выйти и порезвиться на улице. Они говорили, что Линда со Стивом соскучились по мне, но вряд ли это было так. Всё лето они проводили на улице: просыпались на заре под пение соек и дроздов и целый день играли то в догонялки, то в прятки, пока в сумерках не зажигались блуждающие огоньки светлячков. Нет, я им был не нужен.

Теперь у меня появилась цель: я ничем не мог помочь Рути, но мог придумывать лекарства от болезней и спасать других людей. В двенадцатилетнем возрасте серьезно настроенный мальчик может проявлять недюжинную решимость, и я был готов идти до конца.

В том же году в учебнике алгебры мне попалась одна дополнительная задача. Чуть ли не все выходные я пробовал разные изощренные способы ее решения. Наконец у меня получилось, но как-то неуклюже, механистически, неизящно. Ответ сошелся, но я понимал, что автор имел в виду нечто другое. В понедельник после урока математики я подошел к учительнице. Она улыбнулась и сказала, что рада моей попытке решить задачу, а потом показала простое и красивое решение.

В тот момент весь мир для меня словно схлопнулся, исчез, и я почувствовал некий новый привкус печальной горечи. В решении использовались только известные мне способы, но мне даже не пришло в голову применить их таким образом. С того дня я начал подозревать, что недостаточно умен и не смогу стать хорошим ученым. Благодаря своей целеустремленности и трудолюбию я вполне мог войти в ученую среду, но удовлетворит ли меня жизнь на вторых ролях? Выбор такой карьеры вполне мог привести к тому, что в конце своего жизненного пути (где я сейчас и нахожусь), оглядываясь назад, я увижу лишь долгие годы кропотливой работы с весьма редкими вкраплениями скромных озарений. Несомненно, это были бы восхитительные мгновения. Наслаждение от того, что ты хоть немного проник в архитектуру идей, само по себе щедрая награда. Но мне хотелось чего-то большего.

Была ли моя жизнь так уж непохожа на жизнь других людей? Бывает так, что возможности и интересы человека совпадают, его полностью устраивает его жизнь безо всяких сожалений и сомнений – такому можно лишь позавидовать. Но многих из нас одолевают мысли об упущенных возможностях. Некоторые решения приводят нас туда, откуда нет пути назад. Даже если мы сейчас изменим траекторию, остаток жизни пройдет не так, как если бы много лет назад мы сделали иной выбор. Нам больше недоступно то, что могло бы произойти, и мы испытываем горечь утраты.

Путь, который выбрал я, – то есть исследование некоторых математических структур, – открыл для меня новые горизонты скорби. Мне кажется, переживание утраты имеет сходные черты с занятием математикой; мы увидим, как одно перекликается с другим. Когда я бился над какой-либо математической задачей, это помогало мне разобраться со своей болью. Об этом моя книга.

В своем «Альманахе для сомневающихся» Этан Канин^[3] пишет:

Вызывает ли смерть ту же горечь, что и мысль о страданиях, которые ждут ребенка в будущем? А грусть, которую навевает музыка? Это та же грусть, что приходит к нам в летних сумерках?.. И то и другое мы зовем скорбью…

Но как утолить боль, которую я испытываю о моем отце в последние несколько дней? Мы думаем, будто наша скорбь, подобно всем плоскостям, известным нам в этом мире, имеет границы. Но так ли это?^[4]

Поскольку геометрия, с моей точки зрения, самая красивая часть математики и та часть, которую я знаю лучше всего, я в основном буду говорить о геометрии – о геометрии скорби. Она столь же отличается от «скорби геометрии» (это когда вы испытываете томительное желание вырваться с последнего урока, где учитель дотошно разбирает на доске в две колонки доказательство «по двум сторонам и углу между ними»), как слова известного блюза «If it weren’t for bad luck, I’d have no luck at all»^[5] от арии «Nessun dorma» Пуччини. В этой книге мы рассмотрим, каким образом геометрия и скорбь раскрывают некоторые аспекты друг друга.

Мой проект был уже почти полностью оформлен еще до того, как я решил поинтересоваться, что на данную тему писали другие. В этой книге часто повторяется такая мысль: идея никогда не возникает на пустом месте. Если бы я воспринял чужие идеи прежде, чем обдумал собственный опыт переживания скорби, возможно, я не смог бы осмыслить свой опыт достаточно глубоко. Только после того, как я набросал общий план книги, я прочел основные работы по этой теме. Особенно полезными оказались эволюционные исследования психолога Джона Арчера «Природа скорби», антрополога Барбары Кинг «Как животные скорбят», а также врача и биолога-эволюциониста Рэндольфа Несси «Эволюционные основы для понимания скорби»^[6]. Некоторые из моих идей схожи с научно доказанными, некоторые – отличаются, и порой существенно. На них я сконцентрируюсь отдельно.

Можно ли считать проявлением эгоизма то, что я отдал предпочтение собственным размышлениям, а не рассуждениям ученых, посвятивших исследованиям скорби многие годы? Вы можете не согласиться, но я отвечу «нет». В темные часы от полуночи до рассвета мы оказываемся наедине со своими мыслями. Именно в это время мы наиболее полно ощущаем нашу внутреннюю скорбь. Сперва надо разобраться в собственном опыте, и лишь затем сравнить его с уже существующими трудами. Чтобы моя книга была вам понятна, вам надо прежде заглянуть внутрь собственной скорби.

* * *

Несмотря на всё мое восхищение работами Арчера, Кинг, Несси и других ученых, я полагаю, что литература, кино и музыка позволяют более непосредственно и живо погрузиться во внутренний мир скорби. Эту идею разделяю не только я. Когда Александр Шенд^[7] писал «Основы характера», где впервые систематически исследовал психологию скорби, у него было мало экспериментальных данных, так что примеры он брал из поэзии и литературы, из произведений писателей, которые внимательно и тонко относились к наблюдению за человеческой природой^[8]. Арчер прибегает к литературным произведениям, чтобы, используя их мощь, ярче выразить эмоциональную остроту чувства, а также исследует, как скорбь проявляется в искусстве^[9].

Жизненные истории дают нам более непосредственную, более подробную и развернутую картину. О взглядах Сартра на экзистенциализм я узнал гораздо больше из его трилогии «Дороги свободы», чем из серьезного философского труда «Бытие и ничто»^[10]. В дальнейших главах я буду рассказывать много личных историй.

Чтобы понять, каким образом искусство интуитивно передает глубину таких переживаний, как любовь и скорбь, вспомните слова песни «My Skin» Натали Мерчант или ее проникновенный голос в «Beloved Wife». Вспомните печальные, но полные надежды слова «Dante’s Prayer» Лорины Маккеннитт. Вспомните захватывающий финал «Сочленения № 5» из оперы «Эйнштейн на пляже» Филипа Гласса. С музыкальной точки зрения другие части произведений Гласса более интересны, но у меня захватывает дух от наслаивающихся голосов инструментов и прозаичного монолога на их фоне. Музыка способна напрямую донести до нас всю глубину чувств^[11].

Если вы смотрели прекрасный фильм Энга Ли «Крадущийся тигр, затаившийся дракон», вспомните, как Ли Мубай умирает на руках Юй Шулень. Перед смертью он говорит ей такие слова: «Я и так напрасно потратил всю свою жизнь. И на пороге смерти я должен тебе сказать… Я всегда тебя любил. Я лучше буду призраком, бродящим рядом с тобой… как неприкаянная душа… чем поднимусь на небо без тебя. Благодаря твоей любви… я никогда не буду одинок».

Или вспомните концовку. Цзень прибывает в храм на горе Удан. Вместе со своим возлюбленным, разбойником Ло, она стоит на мосту над облаками и спрашивает его: «Ты помнишь легенду о юноше?» Когда-то Ло рассказал ей:

У нас есть легенда: Бог выполнит желание человека, осмелившегося прыгнуть с горы. Некогда родители одного юноши заболели, и он прыгнул. Он не умер. Он даже не пострадал. Он улетел далеко-далеко и не вернулся. Он знал, что его желание сбылось. Если веришь, сбудется. Старики говорят: «Сердце верит – желание сбудется».

Ло: «Сердце верит – желание сбудется». Цзень: «Загадай желание, Ло». Ло: «Вместе вернуться в пустыню». Цзень прыгает с моста и исчезает в облаках. Под прощальные звуки виолончели Йо Йо Ма^[12] она летит сквозь облака. И становится понятно, что это не фильм про боевые искусства, а история о любви, утрате и скорби^[13].

А может быть, вы смотрели «Клиент всегда мертв» – сериал из пяти сезонов о жизни семьи владельцев похоронного бюро в Лос-Анджелесе. Конечно, вы можете возразить, что я выбрал слишком очевидный пример: те, кто занимаются похоронным бизнесом, сталкиваются со скорбью ежедневно на работе. Однако в каждом эпизоде смерть и скорбь рассматриваются с определенной философской или психологической точки зрения. Меня особенно интересует финальный эпизод, где звучит песня «Breathe me» в исполнении Сии^[14]. На наших глазах проходит жизнь и смерть главных героев, мы видим весь их жизненный путь, раскрываются разные грани скорби, она представляется как отзвук любви. Я хотел бы упомянуть и забавную (хотя на самом деле грустную) отсылку к данному эпизоду в «Симпсонах», в последней серии двадцать девятого сезона под названием «Лестница Фландерса».

Вспомните смерть Евгения Базарова в романе Тургенева «Отцы и дети» и неизбывную скорбь его старых родителей, горюющих над могилой сына^[15]. Евгений мог бы избежать смерти. Секундный промах – и в мире романа его смерть стала реальной, неотвратимой. В конце произведения Тургенев так описывает его могилу, расположенную на небольшом деревенском кладбище:

К ней, из недалекой деревушки, часто приходят два уже дряхлые старичка – муж с женою. Поддерживая друг друга, идут они отяжелевшею походкой; приблизятся к ограде, припадут и станут на колени, и долго и горько плачут, и долго и внимательно смотрят на немой камень, под которым лежит их сын…

Душераздирающая картина родительского горя. Но, зная весь контекст романа, мы еще глубже понимаем их отчаяние. Иногда мне кажется, что ощущение этой раздавленности в сочетании с простотой и обыденностью тургеневского стиля раскрывают самую суть великой красоты, таящейся в глубине скорби.

Истории из жизни не могут передать чувства другого человека, но они помогают нам представить, как бы мы чувствовали себя на его месте. Здесь, как мне кажется, кроется суть сопереживания. Только так мы можем что-то понять о природе скорби.

Многое из того, о чем мы будем здесь говорить, выросло из моих собственных интроспективных размышлений, моего опыта переживания скорби и раздумий о геометрии. В основном я буду рассказывать о них на примере личных историй, а не в виде абстрактных рассуждений, поскольку считаю, что жизненные примеры гораздо нагляднее отражают идеи, для понимания которых важны чувства. Абстрактные рассуждения дают определенную основу, а истории из жизни показывают предмет во всей его непосредственности и злободневности.

Возможно, мой опыт напомнит вам свой собственный. А может быть, у вас были совершенно другие переживания. Приводит ли различный опыт к различному пониманию скорби? Я не знаю. Природа дает простор для множества вариантов. А сколько их еще живет в нашем воображении?

* * *

В этой книге мы познакомимся с несколькими идеями, большинство из которых будут изложены несколько раз в различных контекстах и подкреплены примерами из жизни. Вот краткое описание основных моментов, которые мы будем исследовать.

Скорбь – это реакция на невосполнимую утрату. Следовательно, нельзя испытать скорбь заранее^[16]. Чтобы возникла скорбь, а не просто грусть, утрата должна нести большую эмоциональную нагрузку и приоткрывать завесу трансцендентной стороны мироздания. Разгонять туман, заслоняющий от нас средоточие ослепительного света. Мы сфокусируемся на трех аспектах скорби: необратимости, эмоциональной значимости и трансцендентности. Они свойственны не только опыту скорби. У меня самого нет детей, но, по моим представлениям, родительство является не менее глубоким переживанием: та же необратимость, эмоциональная наполненность, трансцендентность. Однако скорбь вдобавок – это реакция на утрату

Скорбь возникла в процессе эволюции. Мы рассмотрим доводы в пользу этой теории, а также доказательства того, что животные тоже скорбят. Кроме того, мы увидим, что литература и музыка порой являются для нас весьма полезными проводниками в мир скорби. Одновременно они помогают справиться с ней.

Момент озарения, когда всё вдруг становится ясно, бывает лишь раз. Но если то, что мы поняли, очень важно для нас, если оно затрагивает тайные глубины души, мы порой скорбим об утрате этого мига: будучи единожды пережитым, он уже никогда не случится вновь. Красота, увиденная в зеркале, отражает скорбь. Именно она, по моему мнению, связывает скорбь с геометрией.

Взгляд на жизнь как на траекторию внутри пространства повествования, который мы вводим в четвертой главе, открывает путь к возможности проецировать свою скорбь на что-либо и тем самым облегчить ее. Пространство повествования – наш основной инструмент, поэтому здесь я перечислю главные тезисы, связанные с ним:

• Каждый момент нашей жизни обладает множеством – возможно, бесконечным множеством – переменных, которые мы способны регистрировать (обнаруживать, осознавать).

• Мы можем представлять себе наши жизни как траектории, пролегающие сквозь пространство повествования, параметризованные временем.

• Мы никогда не можем охватить взором (осознать, зарегистрировать) все возможные переменные; более того, мы фокусируемся только на нескольких переменных, ограничивая свое внимание подпространством малой размерности в пространстве повествования.

• Траектория нашего движения сквозь эти подпространства – то, что мы рассказываем о своей жизни самим себе, то, как мы представляем себе смысл нашей жизни, но в этом рассказе всегда недостает каких-то элементов нашего опыта.

• Необратимая утрата проявляется как разрыв, скачок через пространство повествования (или в пространстве повествования).

• Фокусируясь на определенных подпространствах, проектируя в них наши траектории, мы можем снизить видимую величину скачков и, следовательно, каким-то образом противостоять эмоциональной утрате, а может быть, и уменьшить ее воздействие. В дальнейшем мы проиллюстрируем данный тезис парой примеров.

Более того, скорбь самоподобна: скорбь утраты близкого человека содержит в себе множество более «мелких скорбей». Вы больше никогда не будете беседовать, делиться друг с другом воспоминаниями о плохом и хорошем, не прогуляетесь молча вдвоем. Каждая из этих «скорбей» – уменьшенная версия вашей реакции на утрату близкого, маленькая копия, которая может стать лабораторией для поиска полезных проекций. Спроецированная вовне, скорбь способна указать на те действия, которые помогут другим людям. Мне представляется, что при наилучшем раскладе в данное русло можно перенаправить часть этой энергии скорби. Пусть это будут не большие шаги, а маленькие, но все же шаги вперед.

Моя книга – гимн любви к покойным родным, друзьям, которых нет с нами, и котам, которых мы потеряли. А еще это гимн любви к геометрии, ярчайшей точке моих размышлений. В старости мое понимание геометрии с каждым годом всё больше стирается, добавляя разбитому сердцу еще больше разветвленных трещин.

Представленные здесь примеры из геометрии являются не просто инструкцией о том, как справиться со своей скорбью, они рисуют план действий, который помог мне. Возможно, эти вехи укажут путь, чтобы вы, с помощью моего подхода, смогли сами умерить свою боль. И, возможно, они помогут вам увидеть геометрию в своей жизни там, где раньше вы ее не замечали.

1. Геометрия

Жаль, что уже не увижу деревья, какими видел их раньше.

Представьте, что сейчас ранняя весна, вечерние сумерки, и вы сидите в каком-то малознакомом парке. Что вы увидите, подняв глаза от страницы этой книги? Вероятно, замысловатый узор из светлых и темных силуэтов, вливающихся в шероховатые столбы – стволы деревьев; толстые ветви, ветки потоньше, мелкие прутья; потрепанные обрывки плоскостей – листьев. А еще цветы и траву. Геометрические формы позволяют нам узнавать или, по крайней мере, называть то, что нас окружает.

Мы видим, как зрительно меняются формы, распознаём их движение – наблюдаем, например, как листья и ветки покачиваются от легкого ветерка.

Листья на вершине высокого дерева всё еще освещены солнцем, хотя ствол погружен в темноту. Мы обычно говорим, что тьма спускается, но здесь она как будто поднимается (а если мы придем в парк утром, то увидим, как по стволу дерева спускается рассвет). Геометрия солнца и земли являет во всей простоте то, чего мы раньше не замечали в этом мире.

На протяжении веков художники великолепно чувствовали геометрию. Приведу лишь несколько примеров. А если вы немного покопаетесь в «Гугле», то найдете еще больше.

Построенный в IX, а затем воссозданный в XIII веке дворец Альгамбра в испанской Гранаде – прекрасный образец исламского искусства и архитектуры. Множество декоративных мозаик, включая ту, что приведена ниже, являются замощениями плоскости правильными многоугольниками.

Это фигуры, которыми можно покрыть всю поверхность без наложений и пропусков, поскольку все они соприкасаются друг с другом лишь краями (частично или полностью). Клетки шахматной доски или шестиугольные пчелиные соты – наиболее известные из таких фигур, но есть и другие.

В книге Бранко Грюнбаума^[17] и Джоффри Шепарда^[18]«Плитки и паттерны» (этот семисотстраничный труд вполне заслуживает эпитета «всеобъемлющий») приводится огромное количество примеров не столько из области искусства, сколько из области математики^[19]. Вообще существует семнадцать различных паттернов, обладающих красноречивым названием «группы орнамента». То, что таких паттернов всего семнадцать, было доказано в конце XIX века, но исламские художники знали об этих способах мощения за сотни лет до того, как русский кристаллограф и математик Евграф Фёдоров представил свое доказательство данного тезиса^[20]. Иногда художники интуитивно делают открытия, которые математики проверяют и доказывают лишь многие годы спустя.

Взаимодействие геометрии и искусства отражают также подобные треугольники. Из школьных уроков геометрии мы знаем, что два треугольника подобны, если они имеют одинаковую форму, даже если у них разные размеры. Фигура называется самоподобной, если она состоит из элементов, каждый из которых подобен целой фигуре. На верхнем рисунке слева приведена фигура, состоящая из треугольников, расположенных внутри других треугольников, – это треугольник Серпинского, одна из самых известных самоподобных фигур. Чтобы увидеть ее самоподобие, обратите внимание на то, что она состоит из трех частей – нижней левой, нижней правой и центральной верхней, – каждая из которых подобна целому треугольнику. Об этом треугольнике мы поговорим подробнее в третьей главе.

Фракталы (класс фигур, впервые описанных математиком Бенуа Мандельбротом) – фигуры, построенные из частей, среди которых каждая так или иначе подобна целому. Кусочек береговой линии, если его рассматривать вблизи, выглядит так же, как ее большой отрезок с большого расстояния; листочек папоротника выглядит как сам папоротник в миниатюре; двухметровая нить ДНК сворачивается внутри клеточного ядра диаметром примерно в одну миллионную часть ее длины, повторяя один и тот же способ сложения каждый раз в меньшем масштабе. Это фракталы, которые мы наблюдаем в природе. Простейшие фракталы – самоподобные фигуры вроде треугольника Серпинского.

Круглый узор под треугольником на рисунке слева – это плиточный орнамент XIII века в одном из итальянских соборов, представляющий собой шесть фигур, напоминающих изогнутые треугольники Серпинского, окруженные кольцом треугольников поменьше^[21]. (Делая данный набросок, я измерил и зарисовал основные элементы, а остальное заполнил на глаз. Это заняло немало времени. Но оригинал вырезался вручную, элемент за элементом, а потом они складывались вместе. Когда я об этом думаю, тот час, что я провел над рисунком, уже не кажется таким долгим.)

Художники размышляли над самоподобием многие века. Почему? Потому что оно часто встречается в природе, а художники внимательно присматриваются к ней.

Более свежим примером использования самоподобия является картина Дали «Лицо войны» (1940), изображающая бесчисленные ужасы гражданской войны в Испании. На картине мы видим лицо, в глазницах которого и во рту заключены другие лица, в чьих глазницах и ртах снова заключены лица, и так далее еще на несколько уровней вглубь. Паттерн очень напоминает треугольник Серпинского – повторение фигур, выстроенных в треугольник, только в данном случае располагающихся наверху слева и справа и внизу посредине. Картина Дали гораздо страшнее, чем мой набросок: по обеим сторонам головы без тела вьются клубки змей^[22].

На предварительном эскизе картины только рот заключал в себе другое лицо. В одной из глазниц располагались кольца древесного ствола, а в другом – пчелиные соты. Дали обнаружил, что повторяемость самоподобия – наглядный способ показать бесконечность.

Чтобы показать скрытую бесконечность, Дали придумал своего рода замощение. За пять веков до него итальянский архитектор Филиппо Брунеллески открыл геометрический способ изображения того, как мы видим объекты. В 1415 году, создавая рисунок флорентийского Баптистерия, он с помощью остроумного приспособления из зеркала и крохотного отверстия, возможно, первым в эпоху Ренессанса открыл (заново) перспективную геометрию^[23]. Некоторые историки-искусствоведы полагают, что древнегреческие и римские художники понимали законы перспективы; другие считают, что их представления о перспективе были примитивными. В средневековом искусстве размер фигур часто соответствовал их религиозной или политической значимости и никак не соотносился с взаимным расположением данных фигур. Идея Брунеллески состояла в том, что живопись должна изображать объекты такими, какими мы их видим. И ключом к этому является перспективная геометрия.

Но в отличие от нее четырехмерная геометрия, казалось бы, не укоренена в нашем опыте, поэтому часто она считается сложной для понимания. Прекрасным введением в этот предмет может стать книга математика Томаса Банхоффа «По ту сторону третьего измерения: геометрия, компьютерная графика и высокая размерность»^[24]. Среди множества способов представления четырехмерного куба (или гиперкуба) Банхофф описывает метод развертки. Куб (то есть его поверхность, а не внутренняя сторона) имеет развертку в виде шести квадратов, что и продемонстрировано на рисунке слева. Гиперкуб, как показывает Банхофф, разворачивается в виде восьми кубов, что видно на рисунке справа. Но почему граница гиперкуба состоит из восьми кубов? Объяснение будет дано в приложении, но, возможно, вас удовлетворит такая последовательность: граница (двумерного) квадрата состоит из четырех (одномерных) отрезков, а граница (трехмерного) куба – из шести квадратов, так что границей (четырехмерного) гиперкуба являются восемь кубов.

Известно, что Дали увлекался наукой и математикой; Банхофф лично и посредством переписки обсуждал с ним вопросы четырехмерной геометрии. Искусство и геометрия – хорошие союзники. На картине Дали «Распятие» (1954), набросок с которой приведен на следующей странице, крест представлен в виде развертки гиперкуба^[25].

Чем не повод начать изучать геометрию? Вы можете даже пообщаться с Дали. Ладно, пусть не с самим Дали – он умер в 1989 году, – а с какой-нибудь другой знаменитостью. Я часто тусовался за кулисами «Шуберт Театра» в Нью-Хэйвене с актером Деметри Мартином, известным своим участием в программе «Дэйли Шоу», потому что он учился у меня фрактальной геометрии.

* * *

Ради последнего примера мы перенесемся где-то на 2300 лет назад, в Александрию, на родину греческого математика Евклида. Поскольку именно он заложил основы геометрии.

Наука, которую мы изучаем в школе, называется «евклидова геометрия». Все ее разделы – построения, масса теорем о треугольниках и всё остальное – вытекают из пяти аксиоматических предпосылок, так называемых евклидовых постулатов. Первые четыре просты и очевидны: любую пару точек можно соединить прямой линией, отрезок линии можно бесконечно продлевать по прямой, любой отрезок прямой является радиусом окружности, все прямые углы равны между собой.

Пятый, называемый «аксиомой параллельности», – постулат иного рода. Он гласит: для любой точки P, не лежащей на линии L, существует только одна линия M, проходящая через P, которая не соприкасается с линией L. Мы говорим, что M параллельна L. Это логично: если хоть немного наклонить линию M в том или ином направлении, в конце концов она пересечется с линией L.

Постулат параллельности отличается от четырех других евклидовых постулатов, он более сложен. В XIX веке некоторые математики попытались доказать, что пятый постулат вытекает из первых четырех. Их попытки были обречены на провал, поскольку существуют системы геометрии – так называемая неевклидова геометрия, – для которых аксиома параллельности является ложной^[26].

При создании ксилографии «Предел – круг III» (1959) М. К. Эшер использовал неевклидову геометрию^[27]. Долгое время художник экспериментировал, пытаясь разными способами представить бесконечность в конечном пространстве. Шахматная мозаика подразумевает бесконечное повторение паттерна, однако в работе Эшера бесконечность не просто подразумевается.

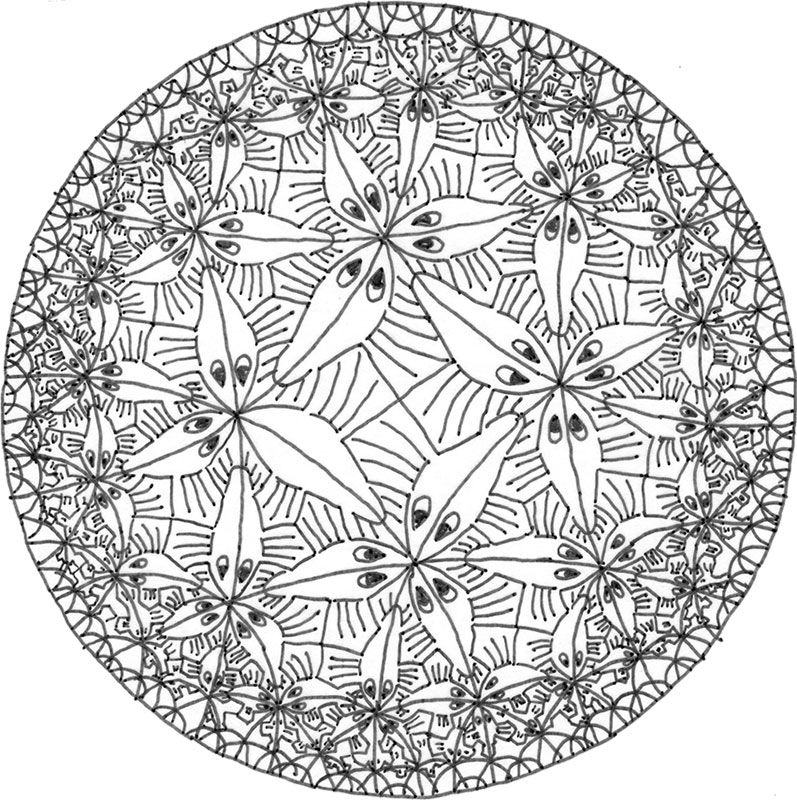
Художник нашел решение благодаря «диску Пуанкаре», придуманному блестящим французским математиком Анри Пуанкаре. Внутри такого диска заключена вся бесконечность плоскости: по мере приближения к его краю (если говорить о приближении в смысле привычной нам евклидовой геометрии) линейка сжимается. Расстояние от центра диска до его края, измеренное линейкой Пуанкаре, будет фактически бесконечным. А площадь диска Пуанкаре также бесконечна. И это не единственное отличие от геометрии Евклида. В диске Пуанкаре прямые линии представлены двумя формами: в виде прямых линий, проходящих через центр диска, и в виде дуг окружностей, которые пересекают его границу под прямыми углами.

Погодите, но как дуги могут быть прямыми линиями? Перед нами пример одного из главных методов развития математики: взять идею из какого-либо контекста – скажем, прямые линии на плоскости – и придумать, как перенести ее в другой контекст. Какое свойство прямых линий мы можем считать общим? В евклидовой геометрии прямая линия – кратчайшее расстояние между двумя точками. Давайте это используем. Вероятно, вы уже знакомы с этим общим свойством, если летали на большие расстояния. Дугой большого круга сферы является любая окружность, центр которой совпадает с центром данной сферы. Все меридианы – дуги большого круга, тогда как единственная параллель, являющаяся такой дугой, – экватор. На поверхности сферы кратчайшее расстояние между двумя точками – дуга большого круга, проходящая через эти две точки. Натяните резинку между двумя точками на мяче: это будет кратчайший путь на поверхности сферы между этими двумя точками. И такой кратчайший путь является дугой большого круга.

Для сокращения времени полета и расхода топлива траектории дальних перелетов пролегают по дугам большого круга. Например, Лос-Анджелес находится на 34,1° с. ш., Москва на 55,8° с. ш., однако полет между этими городами пролегает через север Гренландии, около 70° с. ш.

Но вернемся к диску Пуанкаре. Если измерять расстояния линейкой Пуанкаре, кратчайший путь между двумя точками является либо отрезком диаметра диска, либо дугой окружности, перпендикулярной границе диска. С точки зрения диска Пункаре такие линии будут прямыми.

Почему это неевклидова геометрия? Мы видим, что на диске Пуанкаре для любой точки P, не лежащей на заданной линии L, существует множество – на самом деле, бесконечное множество – линий, проходящих через точку P и параллельных линии L (другими словами, не пересекающихся с линией L). Примерами таких линий являются показанные ниже линии M и M'.

Возможно, из школьного курса геометрии вы знаете несколько теорем (помните: две стороны и угол между ними?), которые доказывают, что два треугольника равны, то есть одинаковы по форме (подобны) и по размеру. На диске Пуанкаре всё немного проще: подобные треугольники всегда равны. Следовательно, если посмотреть на рисунок Эшера, рыбки, которые становятся всё меньше по мере приближения к краю диска, при измерении линейкой Пуанкаре оказываются одинакового размера.

Эшер увидел изображение диска Пуанкаре в одной из работ математика Гарольда Коксетера^[28], а затем в письмах они вместе обсуждали неевклидову геометрию. Хотя в работе «Предел – круг III» Эшер допустил некоторую художественную вольность (как указал Коксетер, кривые, изображенные Эшером, не совсем неевклидовы), в ней прослеживается математическая идея.

Пару слов о моем наброске. У Эшера рисунок с рыбками продолжается до самого края, хоть и не беспредельно, поскольку тогда ему потребовалось бы изобразить бесконечное количество рыбок. Однако у Эшера рисунок гораздо более скрупулезный, нежели у меня. И я должен напомнить, что он работал в технике, не прощающей никаких ошибок. Я уже говорил, какой кропотливой работы потребовало создание мозаики с треугольниками Серпинского в соборе Альгамбры. И всё же, если какая-то плитка была вырезана неправильно, мастер в любой момент мог вырезать другую при условии, что у него было достаточно камня. Однако Эшер работал в технике резьбы по дереву, каждую рыбку он вырезал из одного куска древесины. Одна ошибка могла испортить всю работу, а не какую-то крохотную деталь. Подумайте об этом, когда вам нужно будет набраться терпения.

* * *

Геометрия – способ структурирования наших представлений о мире, о его формах и динамике. Но нет ли во всем этом большой доли случайности, шаткой неопределенности? Могли ли у нас сложиться совсем иные представления о мире? Если бы фрактальная геометрия Мандельброта была открыта раньше, чем геометрия Евклида, производили бы мы то, что производим сейчас? Думаете, это вопрос из области фантастики? Тогда посмотрите, как повторяются разветвления нашей легочной, кровяной и нервной систем, как складываются нити ДНК, подумайте, как огромные по площади ткани легких или кишечника умещаются в небольших объемах человеческого тела. Фрактальная геометрия придумана эволюцией и используется ею. Если бы вместо того, чтобы пытаться достичь «небесного совершенства», навязанного церковным истолкованием работ Евклида и Аристотеля, люди внимательнее присмотрелись к геометрии природы, наши творения ныне были бы абсолютно иными.

Можно ли сказать, что в совершенно несхожих космологических представлениях различных культур отразились разные восприятия, разные геометрии? Или это просто альтернативные пути, обусловленные историческими нарративами? Но если не существует одной-единственной геометрии, одной-единственной истории – если мир не един, – наши представления о нем должны определяться разными наборами категорий.

Именно здесь находится ключевая точка нашего рассуждения. Действительно ли мир такой, каким мы его представляем, или он другой? Должен ли мир быть лишь чем-то одним, или он являет собой множество? Если у нас уже есть определенное представление о мире, оно навсегда отсекает возможности увидеть его другими способами? В квантово-механической модели множественности миров, наглядно описанной в прекрасной книге Шона Кэрролла^[29] «Квантовые миры и возникновение пространства-времени», любое наблюдение за любой из частиц расщепляет Вселенную на ответвления, у каждого из которых будет свой результат измерения, и эти ветви не могут между собой сообщаться^[30]. Таким образом, в физике мы имеем модель, где каждый выбор отсекает от нас все другие. Но действует ли данное разделение в мире людей, в мире облаков, в кошачьем мире? В дальнейшем мы об этом поразмышляем.

Это возвращает нас к теме скорби, реакции на безвозвратную утрату. Неужели вдумчивое изучение геометрии необратимым образом накладывает печать на наши представления о формах мироздания? В математике фантазия гораздо сильнее приближена к исследованию, чем в естественных науках. Здесь, как и в любой науке, необходимо приобрести базовые навыки. Однако математика избавляет от необходимости придумывать эксперименты, монтировать оборудование, проходить этическую экспертизу тех, кто намерен ставить опыты на живых объектах, подвергаться проверкам на безопасность и затем проводить эксперимент, собирать данные, и расшифровывать его результаты. В математике вы просто начинаете размышлять. Ну хорошо, в наше время порой вам приходится писать код, запускать процесс моделирования, но это тоже умственный процесс, а не физический, если не считать набора кода на клавиатуре компьютера. Мы изучаем миры, находящиеся у нас в голове. Исследуя какой-то один мир, мы отсекаем все остальные потенциальные миры, и эта утрата становится источником скорби при изучении математики. Это, конечно, не такая большая скорбь, какую мы ощущаем, потеряв близкого человека или питомца, но, тем не менее, тоже горькое чувство.

Вы можете подумать: как это глупо. Да и что такое – утрата? Разве мы не можем изменить направление своих мыслей в любой момент? В какой-то степени да, но стоит нам посмотреть на мир новым взглядом, и мы уже не можем избавиться от собственного ви́дения. Для наглядности приведу пример из фрактальной геометрии. Если вы не фанат геометрии, можете заменить ее любой другой столь же сложной и утонченной сферой деятельности по вашему вкусу.

Пока что не обращайте внимания на линии решетки, расчерчивающие рисунок на следующей странице. По-вашему, это простая или сложная фигура? Если она кажется вам простой, значит, вы можете точно объяснить, как ее нарисовать. Готовы?

А теперь посмотрите на решетку. Обратите внимание, что пять квадратов пусты. Оказывается, это почти всё, что нам требуется знать: стоит присмотреться к этим пустым квадратам, и мы сможем дорисовать всю фигуру. Это совсем несложно.

Начнем с решетки четыре на четыре квадрата. Сначала оставим пять пустых квадратов и полностью закрасим остальные одиннадцать. Получим картинку, изображенную на следующей странице первой в верхнем ряду. Затем уменьшим ее вдвое, скопируем и разместим одну копию слева, а две другие над первыми двумя. Результат представлен на картинке в центре первого ряда. Наконец из данной картинки вырежем пять больших квадратов, как это сделано на первой картинке. Получилась картинка справа.

Повторяем второй и третий шаги, каждый раз изменяя только что созданную картинку: берем последнее полученное изображение; уменьшаем его в два раза; копируем и размещаем одну копию слева, а две другие над первыми двумя и, наконец, вырезаем пять квадратов, как это было на самой первой картинке. На предыдущей странице вы видите, как начальное изображение изменяется на протяжении первых пяти повторений данного процесса. С каждым повторением фигура приближается к той, которую я показал вам в самом начале. Можно заметить, что малые элементы фигуры похожи на всю фигуру в целом. Если вы решили, что перед вами фрактал, так и есть^[31].

Можно это представить как «фрактальную скуль-птуру». Говорят, Микеланджело утверждал, будто внутри каждого камня заключена скульптура. Мы только что продемонстрировали – для создания данного фрактала нужен лишь набор пустых квадратов и ряд повторяющихся действий. Получившаяся фигура может казаться сложной, но с этой точки зрения она проста. Не стоит удивляться, что то, насколько сложным выглядит объект, зависит от инструментов, с помощью которых мы его анализируем.

Стоит научиться распознавать фрактальные элементы объектов, и ваше восприятие поменяется навсегда. За многие годы я получил десятки мейлов от приятелей моих студентов с вариациями одной и той же жалобы: «Каждый раз, когда мы идем на занятия, мой сосед по комнате замечает какой-нибудь папоротник, или облако, или трещину на дорожке, и наш разговор прерывается восклицанием: „Это фрактал! Это фрактал!“ Прекратите уже рассказывать об этих фракталах! Сколько хороших бесед вы разрушили». Меня обвиняют в том, что я засоряю умы гуманитариев геометрией.

* * *

Я твердо полагаю, что фракталы невозможно игнорировать, как только вы их увидели. Они навсегда меняют картину мира, которая разворачивается в нашем сознании, навсегда меняют вид тех моделей, что мы выстраиваем.

Впервые я по-настоящему понял это на уроке геометрии в старших классах школы. Некоторое время мы занимались построениями с помощью циркуля и линейки: такие головоломки очень любили древние греки. Мы научились делить отрезки на две, три, четыре и любое количество равных частей. Затем наш учитель, мистер (Ральф) Гриффит, рассказал, что древние греки придумали три задачи, которые они не смогли решить: трисекцию угла (построение угла величиной в одну треть от заданного), квадратуру круга (построение квадрата той же площади, что и заданный круг) и удвоение куба (построение куба с объемом в два раза больше, чем у заданного).

Пока я ломал голову над этими задачами, у меня появилась идея. Возьмем угол AOB: проведем прямую линию от A до O и затем прямую до точки B (см. рисунок на следующей странице). Чтобы разделить угол AOB на три равных угла, подумал я, надо просто разделить на три части отрезок AB – отрезок прямой, соединяющий точки A и B. То есть найти на этом отрезке такие точки C и D, чтобы длина BC совпадала с длиной CD и длиной DA. Ведь мы как раз научились это делать. Тогда, предполагал я, углы AOD, DOC и COB будут равны, а следовательно, угол AOD будет равен одной трети от угла AOB. То, что эта простая идея – на самом деле, первое, что приходит в голову любому, – каким-то образом оставалась незамеченной на протяжении двух десятков веков, не показалось мне чем-то странным и неправдоподобным. У меня даже не закралось никаких сомнений. На мгновение в моем мозгу промелькнул газетный заголовок: «Ученик школы решил задачу, над которой две тысячи лет бились математики».

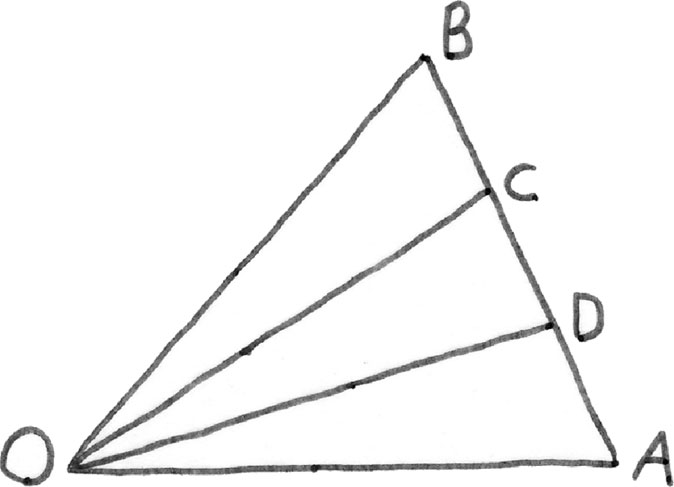
Я показал свои построения мистеру Гриффиту. У меня был крохотный рисунок, сделанный дешевым циркулем. Мой транспортир показывал практически равные углы. Мистер Гриффит с помощью более точного циркуля сделал рисунок крупнее. Его транспортир показал, что углы были неравны. Учитель не сказал: «Если б это было так просто, неужели ты думаешь, что за две тысячи лет никто не догадался так сделать?» Он был рад, что я попытался.

Я предположил, что геометры просто не смогли найти правильный метод. «Нет, – сказал мистер Гриффит, – просто есть такие задачи, которые не имеют решения, и мы можем это доказать». Что? У какой задачи нет решения? Но, что еще поразительнее, как мы можем знать, что у этой задачи нет решения? Никакого. Три года я не мог принять тот головокружительный факт, что существует доказательство неразрешимости некоторых теорем^[32]. Лишь через много лет я всё же понял, почему упомянутые геометрические построения невозможны^[33]. Для доказательства требуется очень сложная математика – неудивительно, что древние греки до него не додумались.

Но в школе я этого еще не знал. А вот о том, что в физическом мире есть невозможные вещи, я знал с пеленок. Я не могу взмахнуть руками и полететь на луну. Да и менее глупые вещи мне порой недоступны: я неуклюжий, напрочь лишен ловкости или хотя бы умелости. Но геометрия… то, что в ней есть нечто невозможное, ставило меня в тупик. Как может быть так, чтобы геометрическая задача не решалась при должном усердии? Если это правда, значит, с нашей вселенной что-то явно не в порядке.

Я спросил мистера Гриффита, как вообще доказать невозможность какой-либо математической конструкции. Он не стал объяснять мне доказательство трисекции угла. Вместо этого учитель рассказал, что квадратный корень из двух нельзя записать в виде соотношения целых чисел (еще один вывод, потрясший основы греческой геометрии). Само доказательство простое, ясное и изящное. (Оно включает в себя немного алгебры; вы найдете его в приложении.) Я был несказанно счастлив, когда мистер Гриффит любезно мне всё объяснил шаг за шагом.

В тот вечер, раздумывая над этим изящным решением, я понял, что у геометрии тоже есть границы. Я расстроился минут на десять. А затем осознал, что эти границы делают геометрию еще интереснее. Насколько именно интереснее, я не представлял себе еще многие годы и до сих пор не до конца понимаю. Оказывается, то, что я считал схематическим изображением целого мира, описывало лишь его крохотный уголок.

На следующий день по дороге в школу я прокручивал в голове этапы доказательства. Все части по-прежнему прекрасно сочетались друг с другом, но первый восторг узнавания куда-то исчез – тот самый, который некоторые называют моментом озарения. Миг, когда наблюдения или идеи сами по себе вдруг складываются в новую картину, кристально очевидную, но невидимую ранее. Эта новая идейная конструкция остается с вами навсегда, а момент озарения – нет. Для каждой идеи может быть лишь один момент озарения.

Когда я преподавал фрактальную геометрию, вторая лекция содержала самый мощный момент озарения за весь семестр. Суть озарения заключалась в серии картинок, показывающих, как силуэт кота превращается в треугольник Серпинского^[34]. Несколько недель спустя, когда мы изучали другие темы, порой весьма сложные, студенты жаловались на то, что им хотелось бы видеть побольше сюрпризов наподобие того, что я показал на второй лекции.

С другой стороны, вернуться к прежней модели устройства мира, игнорируя новую (фракталы), бывает весьма затруднительно. Мне сотни раз приходилось слышать сетования вроде: «Жаль, что я больше не смогу, глядя на деревья, просто любоваться их красотой. Теперь я невольно ищу трансформации, в результате которых возникает форма дерева». Как хорошо, говорят эти студенты, что Джон Мьюр^[35] (или Рейчел Карсон^[36], или Эдвард Эбби^[37]) не знали о фракталах. После столь сильного удара по сознанию вы какое-то время будете неспособны забыть эту новую идею.

Мартин Гарднер^[38], который практически каждый месяц с января 1957-го по июнь 1986 года вел колонку «Математические игры» в журнале «Сайентифик америкэн», составил сборник математических задач под названием «Есть идея!»^[39]. Его задачи остроумные, требующие нестандартных решений и занимательные – для тех, кто любит математические головоломки. Но эти крохотные озарения не вносят необратимых изменений в наше видение мира.

Или всё же вносят? Возможно, они не меняют представления о мире в целом, зато позволяют нашему воображению избавиться от очевидных, но слишком громоздких подходов к решению проблем. На этот счет я приведу в пример так называемую задачу о шмеле.

Представьте: с востока на запад проложена совершенно прямая железная дорога длиной 50 миль. С ее западного конца на восток отправится локомотив, который будет ехать со скоростью 30 миль в час; с восточного конца ему навстречу поедет локомотив со скоростью 20 миль в час. Оба локомотива отправляются ровно в полдень. Также ровно в полдень с передней части локомотива, движущегося на восток, слетает шмель и летит вдоль железной дороги со скоростью 70 миль в час. Долетев до локомотива, идущего на запад, он разворачивается и летит в западном направлении, пока не встретится с локомотивом, идущим на восток, затем снова разворачивается, летит на восток, встречается с локомотивом, идущим на запад, и так далее (см. рисунок на следующей странице). Оба локомотива движутся без остановок. Вопрос: какое расстояние пролетит шмель, прежде чем локомотивы столкнутся и раздавят его?

С задачей о шмеле я познакомился, когда учился в седьмом классе. В тот год к нам приехали два инженера из НАСА. Полагаю, они искали учеников, склонных к науке и математике. Во время обеденного перерыва ко мне подошел учитель естествознания и попросил побеседовать с этими инженерами перед их дневной презентацией. Один из них рассказал мне условие задачи о шмеле и спросил, могу ли я ее решить.

Ладно, когда шмель летит навстречу локомотиву, идущему на запад, относительная скорость шмеля и локомотива составляет 70 + 20 = 90 миль в час. Им обоим предстоит проделать расстояние в 50 миль, то есть шмель встретится с локомотивом, идущим на запад, через 50/90 часов, то есть через 331/3 минуты. Я знаю скорость шмеля и время полета, значит, могу найти расстояние, которое он пролетел: расстояние = скорость × время.

Кроме того, я могу вычислить, какое расстояние проехал каждый из локомотивов за это время. Сложив эти расстояния, я могу вычесть эту сумму из изначальных 50 миль и получить расстояние, проделанное шмелем и локомотивом, идущим на запад, до того как они встретятся. Я уже был знаком с бесконечной геометрической прогрессией, когда складываются фиксированные кратные предыдущего числа. Например, 1 + 1/2 + 1/4 + 1/8 + … – это бесконечная геометрическая прогрессия, где фиксированное кратное равно 1/2. Если удастся увидеть закономерность и найти это фиксированное кратное, то благодаря несложной формуле можно получить сумму. Однако в задаче о шмеле найти фиксированное кратное совсем не просто. Будь у меня бумага и карандаш, я, возможно, справился бы с этим за час. Таким образом, я понимал, как решить задачу, но это был полный бардак.

Однако у меня не было бумаги и карандаша, а инженер просто спросил, могу ли я решить задачу. Он не сказал: «Не спеши, подумай». Похоже, он ждал ответа прямо сейчас. Что же я упустил? А что если не обращать внимания на шмеля и сосредоточиться на локомотивах? Им надо проехать 50 миль, скорость их сближения составляет 50 миль в час, значит, они встретятся через час. Постойте. Шмель летит со скоростью 70 миль в час, значит, за час он пролетит 70 миль. Так вот что требовала от меня эта задача. Вовсе не решение сложных геометрических прогрессий. И я ответил: «Семьдесят миль». Оба инженера улыбнулись. Один сказал, чтобы я связался с ними, когда окончу колледж. Я с ними так и не связался. Где бы я сейчас был, если б сделал это?

За несколько лет до меня эту же задачу о шмеле задали гениальному математику Джону фон Нейману. Нейман участвовал в Манхэттенском проекте в Лос-Аламосе, работал с Эйнштейном в Институте перспективных исследований в Принстоне и был одним из главных создателей современных компьютеров. Бенуа Мандельброт, создавший фрактальную геометрию, был последним постдок-сотрудником Неймана в Принстоне. Еще с детства Нейман мог в уме перемножать восьмизначные числа. Когда ему предложили задачу о шмеле, он задумался на пару секунд, глядя в пространство, а затем дал правильный ответ. «Значит, вы поняли, в чем подвох», – сказал собеседник. «Какой подвох? – ответил Нейман. – Я нашел сумму прогрессии». В данном случае гениальные вычислительные способности Неймана не позволили ему увидеть более простое решение.

Возвращаясь из школы домой, я думал обо всём, что произошло: теперь я понимал – некоторые задачи можно решить разными способами, и первое решение, приходящее на ум, может оказаться излишне сложным.

Когда я увидел подвох и нашел верное решение, это было маленькое озарение, которое по-научному можно назвать локальным озарением. А большим, или глобальным, озарением стал момент, когда я понял – очевидный подход к задаче не всегда ведет туда, куда нужно. Раньше, едва увидев стратегию решения, я тут же бросался в работу. И даже теперь, сорок пять лет спустя, найдя первый вариант стратегии, я чувствую, что могу перевести дух и позволить фантазии поиграть с задачей: вдруг найдется иной способ? Когда на занятиях мы приступали к какой-то трудной задаче, а затем находили первое решение, я всегда просил студентов поискать другое. «Зачем?» – удивлялись некоторые. Чтобы, возможно, найти более простое и, сравнив эти два решения, увидеть то, чего мы раньше не замечали в задаче. Стоит свернуть за угол, и обратной дороги не будет. Я думаю – надеюсь, – что некоторые из моих студентов это поняли, хотя большинство, похоже, так и не осознали, зачем тратить время на поиски иного решения. Многие отказывались его искать.

Но разве наша приверженность привычному образу мысли означает, что мы не должны узнавать новое? Конечно же, узнавать новое надо. Старые способы ви́дения мира отбрасываются за ненадобностью, потому что перед нами открываются новые. Только так мы постигаем мир. Однако неизбежное закрытие некоторых дверей не должно побуждать нас к отказу от альтернативных решений и толкований. И хотя наша жизнь априори подразумевает многочисленные утраты, невосполнимая утрата всегда невыносима.

Вас может несколько удивить, что геометрия способна дать представление о том, как мы понимаем природу. Однако цель данной книги в другом, во всяком случае, это не главная ее тема. Я хочу показать, что геометрия способна помочь нам осознать собственное ощущение утраты. Но прежде мы покажем, как с помощью геометрии можно неожиданным образом истолковать литературное произведение.

Рассказ Хорхе Луиса Борхеса «Круги руин» (1940) занимает в авторском сборнике «Лабиринты» чуть больше пяти страниц^[40]. Это удивительная фантазия о человеке, который хочет из своих снов создать другого человека во плоти. Если вы еще не читали это произведение, обязательно прочитайте.

Известно, что Борхес хорошо знал математику^[41]. Его увлекали парадоксы и головоломки, особенно те, что связаны с бесконечностью^[42]. В изобразительном искусстве проявления геометрии видны гораздо отчетливее, нежели в литературе. И это неудивительно: изобразительное искусство оперирует формами – видимыми и невидимыми нашему глазу, находящимися в центре и на периферии композиции. Мы можем увидеть всю картину в целом, а можем обратить внимание на какой-либо отдельный фрагмент. А вот литература, как и музыка, воспринимается последовательно. Если у нас нет столь глубокого, досконального понимания всего произведения, чтобы удержать его в голове целиком, мы воспринимаем его по кусочкам, один фрагмент за другим. Чтобы увидеть более крупные паттерны, необходимы память и дедукция. Остановимся пока на литературе. Мы вынуждены делать выводы, располагая весьма ограниченным количеством информации – совокупностью слов рассказа, возможно, корпусом текстов автора и некоторыми сведениями о его жизни. Мы не можем спросить Борхеса, правильно ли понимаем его текст. Нам остается лишь анализировать собственные домыслы и искать подтверждения своим догадкам.

«Круги руин» – это рассказ о человеке, который покидает свой дом в одной из бесчисленных деревушек, разбросанных по крутым горным склонам, и спускается по реке к руинам круглого храма. Его цель – заснув, увидеть человека во всех подробностях и ввести его в реальный мир. Первая попытка – когда он представил во сне группу учеников, а затем выбрал из них одного подающего надежды, – провалилась. Зато вторая – когда он целый год скрупулезно, орган за органом анатомически выстраивал человека – удалась. Божество храма – лошадь, тигр, бык, роза и гроза в одном лице (отличный пример того, как раскрывается фантазия Борхеса: простой перечень слов вдруг приобретает неожиданное значение, и мы застываем в удивлении), называемое – Огонь, – оживило созданного в сновидениях человека. Лишь Огонь и сновидец знали, что он призрак. Два года сновидец учил свое создание, а затем заставил его забыть о времени учения и отослал вверх по реке к другому разрушенному храму, тоже посвященному Огню. Через некоторое время он услыхал о кудеснике, который жил в том храме и которого не обжигал огонь. А вдруг его ученик поймет, что он всего лишь сновидение? Тогда Огонь окружил храм сновидца, но пламя его не сожгло. И сновидец понял, что он тоже лишь призрак, который видится кому-то во сне.

* * *

Давайте разберемся в истории, где создатель своего сновидения сам является чьим-то сновидением. Способна ли геометрия помочь нам увидеть в данном рассказе нечто новое, нечто спрятанное? То, что сновидец является сновидением, геометрически можно представить как:

1 Единичное явление. Сновидец и его сновидение составляют единую историю. Нет ничего иного.

2 Бесконечную череду сновидцев. Сновидец и его сновидение являются частью бесконечной череды сновидцев, видящих во сне других сновидцев.

3 Цикличность. Сновидец и сновидение – одно и то же, время идет циклично, но на каждом круге возникают некоторые отклонения, вариации.

4 Замкнутость в виде ленты Мёбиуса. Сновидец видит во сне сновидение, а сновидение видит во сне сновидца.

Рассмотрим все варианты по очереди. Не забывайте, что мы делаем выводы лишь о том, как, по нашему мнению, каждое из геометрических представлений коррелирует с фантазией Борхеса. Кто-то из читателей может прийти к другим умозаключениям.

Единичное явление. Существует некий протосновидец, который видит во сне главного персонажа рассказа. То есть протосновидец видит во сне сновидца, который, в свою очередь, видит человека, созданного им во снах. А как же этот человек, неужели он никого не видит во сне? Для сюжета, порожденного фантазией Борхеса, это слишком грубая, неизящная, асимметричная структура. Вряд ли можно поверить, что столь искусный рассказчик станет тратить свой прекрасный слог на столь банальную идею.

Бесконечная череда сновидцев. Есть старый анекдот про одного ученого (этот анекдот рассказывали и про Бертрана Рассела, и про Карла Сагана, и про многих других), которому после лекции по астрономии один из слушателей сказал, что вообще-то земля покоится на четырех слонах, стоящих на спине гигантской черепахи. Вежливо улыбнувшись, ученый спросил: «А на чем стоит черепаха?» – «Вы очень умны, но черепаха стоит на другой черепахе и так до бесконечности», – ответили ему.

Мы не знаем, слышал ли Борхес этот анекдот, но такой сюжет в разных формах бытовал по меньшей мере с середины XIX века. И Борхес, несомненно, был знаком с основами арифметики бесконечных чисел^[43]. Но мы обнаруживаем две причины, по которым данная модель вряд ли легла в основу борхесовского сюжета.

Первая – то, что мы называем у Борхеса ощущением честной игры. Если существует бесконечное количество сновидцев и порожденных ими сновидений, мог ли он рассказать нам лишь об этих двух и не упомянуть остальных? Не дать никакого намека на их судьбы, на связь между ними – ничего. Какой смысл рассказывать о двух персонажах, если бесконечное число других навсегда скрыто, даже принципиально непознаваемо? Конечно, Борхес был знаком с «бритвой Оккама» – принципом, который обычно выражается так: «Самое простое объяснение является наиболее вероятным». Однако по-настоящему утверждение Уильяма Оккамского звучало (в переводе с латыни) так: «Не следует умножать сущности сверх необходимого». Это в точности соответствует нашему случаю: бесконечный сонм лишних персонажей бесконечно удаляет нас от структуры, согласующейся с принципом «бритвы Оккама»^[44].

Вторая – проблема времени. Сновидец из рассказа «Круги руин» пребывает в иллюзии своей реальности дольше, чем тот, кого он видит во снах. Если двигаться по цепочке дальше, это время будет становиться всё короче и в конце концов станет невозможно кратким. А если двигаться в обратную сторону, оно будет бесконечно растягиваться, что тоже проблематично.

Цикличность. Возможно ли, чтобы сновидец и его сновидение были одним и тем же? Получился бы замкнутый круг^[45]. Борхес знал об идее цикличности времени. Одно из его эссе так и называется: «Циклическое время»^[46]. В нем он ставит под вопрос фундаментальную идею «подобных, но не тождественных циклов». Каждый новый цикл демонстрирует небольшие отклонения от предыдущего цикла. Но насколько эти отклонения невелики? Сновидец и человек, увиденный им во снах, приходят каждый в свой разрушенный храм, имея за плечами разный опыт, – это отклонение невелико. О сновидце сказано: «Когда бы кто-нибудь спросил, как он зовется, чем занимался раньше, он не нашелся бы с ответом»^[47]. А про человека, созданного в его снах: «Маг [сновидец] побудил его [сновидение] забыть о времени учения». Никто из них не знает, что с ним было до того, как он вошел в храм, так что эта разница несущественна в отношении их судеб.

С другой стороны, у сновидца и у человека, созданного в его снах, были существенно разные периоды, когда каждый из них думал, что он реален. Эта разница могла наложить заметный отпечаток на их судьбы – а как иначе? – то есть, с нашей точки зрения, это важное отличие. Сновидец и его сновидение не могут быть одним и тем же. Значит, рассказ Борхеса строится не на круговой цикличности.

Замкнутость в виде ленты Мёбиуса. До сих пор мы предполагали, что существует только два различных персонажа – сновидец и человек, созданный в его снах.

В первом сценарии мы подняли вопрос о симметрии, а именно: почему человек, созданный в сновидении, не создает своего человека из сновидений. Чтобы не допустить бесконечной череды сновидцев и не столкнуться с проблемами, упомянутыми в разборе второго сценария, очевидным решением является петля: сновидец видит во сне человека, а тот человек видит во сне сновидца. На моем рисунке схематически представлена геометрическая фигура, называемая лентой Мёбиуса, у которой имеется всего один край и всего одна сторона. (Возможно, вы помните ленту Мёбиуса по урокам математики или ИЗО в начальных классах: надо взять длинную и неширокую полоску бумаги, свернуть один ее конец на 180 градусов и склеить концы). Спроецировав каждую точку ленты Мёбиуса на координаты времени, мы получим круг: таким образом, оба персонажа могут видеть во сне друг друга. Как мы уже сказали в третьем сценарии, Борхес был знаком с понятием циклического времени. Нам не потребуется вся лента Мёбиуса: над каждой заданной точкой круга (то есть в заданный момент времени) нам надо знать лишь две точки: одна будет обозначать сновидца в заданный момент времени, а другая его сновидение в тот же момент. Геометрически сюжет можно представить в виде контура ленты Мёбиуса. Конечно, пока сновидец в первый раз пытался создать во сне реального человека, этот человек был скорее потенциальным сновидением, нежели настоящим. Мы считаем это небольшим отклонением, учитывая, что найти геометрическое соответствие литературным структурам можно лишь весьма приблизительно.

Вот, к чему мы пришли благодаря нашим геометрическим построениям. И хотя рассказ подводит нас к финальной фразе: «И с облегчением, с болью унижения, с ужасом он понял, что он сам тоже только призрак, который видится во сне кому-то», – эти слова, сперва поражающие нас, не являются концом истории. У нее вообще нет конца: это автономная вселенная, самовоспроизводящаяся, замкнутая в едином цикле, несмотря на возможные в ней незначительные вариации событий. О циклической природе конечных миров Борхес рассуждает в своем эссе «Доктрина циклов», где представляет даже некоторые расчеты. Благодаря геометрии мы смогли прийти к выводу, что в рассказе «Круги руин» отражено это вечное повторение.

Завершая главу, мы скажем, что вечное повторение учит нас не бросаться словом «бесконечность» направо и налево. Если пространство имеет бесконечную протяженность, лучше говорить не о повторяемости во времени, а о вариативных копиях нас самих в пространстве. Мы видим лишь крохотную часть бесконечного космоса: наблюдаемая Вселенная – это то, что нам видно с Земли. С момента Большого взрыва прошло около четырнадцати миллиардов лет. Добавьте к этому результат ранней космической инфляции и получите диаметр наблюдаемой Вселенной примерно девяносто три миллиарда световых лет. (Почему не двадцать восемь миллиардов световых лет? Потому что именно здесь вступает в дело инфляция.)

Если пространство имеет бесконечную протяженность, значит, оно наполнено множеством – на самом деле, бесконечным множеством – параллельных вселенных, которые, вероятно, можно наблюдать с удаленных, но ненаблюдаемых для нас планет. Совокупность всех этих вселенных называется Мультивселенной. Еще одно допущение гласит, что, в очень больших масштабах (гораздо бо́льших, чем скопления галактик, например), материя приблизительно равномерно распределена в пространстве. На это указывают измерения в пределах наблюдаемой Вселенной. Как объясняет Макс Тегмарк^[48] в статье «Параллельные миры», опубликованной в «Сайентифик америкэн», а также – гораздо подробнее – в своей книге «Наша математическая вселенная», исходя из этих двух предположений (о бесконечности пространства и о равномерном распределении материи), на расстоянии примерно в 10¹⁰¹¹⁸ метров (это очень большое число^[49]) от нас находится другая параллельная Вселенная, идентичная нашей^[50]. Идентичная во всём – все ее квантовые состояния такие же, как в нашей наблюдаемой Вселенной. И в ней существует ваша полная копия: человек с той же структурой мозга, теми же нейронными связями, воспоминаниями – он идентичен вам. Более того, существует бесконечное число копий этой идентичной Вселенной, бесконечное число ваших копий. Но я бы хотел обратить внимание на другое.

Во-первых, одно замечание относительно того, из чего, по мнению некоторых космологов (включая Тегмарка), состоят эти параллельные вселенные. Флуктуации энергии вскоре после Большого взрыва, вероятно, привели к определенной степени случайности в начальных условиях, поэтому, если мы заглянем достаточно далеко, то увидим все возможные варианты расположения, не нарушающие законы физики.

Если пространство действительно бесконечно, то на огромных расстояниях существуют параллельные вселенные, идентичные нашей наблюдаемой Вселенной, за одним исключением… Во время лекции я брал кусочек мела, протягивал руку над столом и спрашивал: «Я уроню этот мел или нет?» В какие-то годы я его ронял, в какие-то нет. Но независимо от этого я каждый раз говорил: «Невероятно далеко отсюда существует копия, идентичная нашей наблюдаемой Вселенной, за исключением того, что в ней я совершаю с мелом противоположное действие».

Но дело не просто во мне и дурацком кусочке мела. Представьте любую из возможных вариаций какого-либо вашего действия. Для любого мельчайшего изменения существует параллельная Вселенная, где всё точно так же, за исключением данного изменения и его последствий. И это касается не только вашей жизни, но жизни каждого. И не только одного изменения, а сочетания всех изменений. Причем не только изменений в нашей жизни, но и каждой травинки, каждой песчинки, всего-всего на каждой из планет, каждого завихрения плазмы на каждой из звезд, каждого вращения галактик, рассыпанных в черных безвоздушных глубинах.

Подумайте и еще об одном. Хотя мы умеем манипулировать бесконечными числами, можно ли считать, будто мы понимаем, что есть бесконечность? С тем же успехом я мог бы преподавать полевые уравнения Эйнштейна моей кошке. «Ну что, Биппети, вот тебе определение ковариантной производной». Ничего не получится.

Сделаем напоследок три замечания, прежде чем перейти дальше. В книге Тегмарка «Наша математическая вселенная» продвигается мысль не о том, что математика хорошо описывает Вселенную, а о том, что Вселенная и есть математика. Не всё научное сообщество согласилось с этой точкой зрения, и хотя я тоже пока не могу сказать, что принял ее, идея кажется мне заманчивой.

В этом танце мы можем менять партнеров, заменять бесконечность пространства на бесконечность времени и обратно. Единственной загвоздкой представляется второй закон термодинамики, который гласит, что в изолированной системе энтропия (мера хаоса в системе) либо увеличивается, либо остается неизменной. Загвоздка вот в чем: увеличение энтропии подразумевает, что до этого ее уровень был ниже, а в момент Большого взрыва – намного, намного ниже. Конфигурации с низкой энтропией встречаются реже, чем с высокой энтропией, поскольку существует гораздо больше способов внести в систему беспорядок, чем способов упорядочить ее. Например, существует лишь один способ сохранить вашу кофейную чашку в целости (высокая упорядоченность, низкий уровень неупорядоченности, низкая энтропия) и огромное количество способов разбить ее (высокая неупорядоченность, высокая энтропия). Так почему же, или как так вышло, что в момент Большого взрыва энтропия была настолько низкой? Людвиг Больцман – создатель математического определения энтропии, сформулировавший статистическо-механическую версию второго закона термодинамики, основанную на количественном подсчете состояний в данной энтропии, – нашел смелый подход к этой проблеме. Хоть и не совсем к этой проблеме, поскольку Больцман умер в 1906 году, задолго до того, как Георгий Гамов и Ральф Альфер опубликовали расчеты своей модели Большого взрыва^[51]. Подход Больцмана состоит в следующем: Вселенная почти всегда находится в состоянии высокой энтропии, в состоянии холодного, диффузного, приблизительно равномерного распределения теплового излучения. Но, если время бесконечно, в итоге из случайных флуктуаций возникнут очаги с низкой энтропией. Каким бы невероятным это ни казалось, одна из таких флуктуаций будет сгустком с очень низким уровнем энтропии, подобным предшествовавшему нам Большому взрыву. Как вы, возможно, догадываетесь, таких флуктуаций возникает не одна, а бесчисленное множество во всевозможных вариациях.

Подход Больцмана описан в книге Шона Кэрролла «Вечность. В поисках окончательной теории времени»^[52]. Меня поразили его рассуждения, хотя далее Кэрролл высказывает некоторые возражения против подхода Больцмана. (Найдите в книге Кэрролла главу «Мозг Больцмана» и посмотрите, как красиво он формулирует свои возражения.)

Кроме того, Кэрролл предлагает собственное объяснение, правда до сих пор не принятое всеми космологами. С точки зрения квантовой гравитации (тоже далеко не до конца изученной) само пространство-время подвержено флуктуациям. Некоторые из этих флуктуаций могут являться зародышами новых вселенных, вырастающих из уже существующей: они возникают из состояния низкой энтропии и, расширяясь, превращаются в новые вселенные. Благодаря случайному характеру флуктуаций, порождающих новые вселенные, может возникать бесчисленное множество начальных условий, так что… (продолжить вы уже можете сами).

Вам может показаться, что мы слишком далеко отошли от наших размышлений о скорби, но это не так. В мгновения дикой паники от осознания необратимой утраты любимого существа меня немного утешала мысль, что в какой-то параллельной вселенной или в каком-то далеком будущем существует версия меня, которая нашла способ укротить пламя скорби^[53]. Как бы я хотел поговорить с тем парнем, но, разумеется, не могу. Но, возможно, когда-нибудь я сам стану тем парнем, а возможно, им станете вы. И тогда у нас состоится весьма полезный разговор.

2. Скорбь

Так мы мягко превращаем тех, кого потеряли, в прозрачные тени.

Питер Хеллер

Некоторые думают, что скорбь – всего лишь «прокачанная» грусть. Но я считаю, что скорбь отличается от грусти с точки зрения и психологии, и философии. Мне грустно, если в тот день, когда я планировал пойти на прогулку в парк и провести там приятный часок с романом Мураками, с утра и до самого вечера не прекращаясь льет дождь. Это вызывает досаду, разочарование, но не означает, что прогулка в принципе невозможна: будут и другие дни, и (надеюсь) новые романы Мураками.

Другое дело, когда я стоял у гроба своей матери и знал – знал, – что ее больше нет. Она никогда не поговорит со мной, не заключит в свои материнские объятия – такие уютные и надежные, сопровождавшие меня с раннего детства и до нашего последнего прощания, всего за несколько недель до того, как инсульт внезапно оборвал ее жизнь. Это скорбь, и она необратима.

Вскоре после смерти моей матери одна из студенток попросила меня написать несколько строк о гравитации, чтобы вставить их в свой учебный проект. «В общем, напишите, что пожелаете, главное, чтобы там было слово «гравитация». И я написал о гравитации и о своей маме:

Гравитация удерживает меня на земле. Благодаря гравитации Земля вращается вокруг Солнца, Солнце кружится внутри Галактики, а Галактика движется в Местной группе галактик и так далее.

Благодаря гравитации с неба идет дождь. И снег. Падают осенние листья. И слезы из моих глаз, когда я думаю о том, что тебя действительно больше нет. Куда ты исчезла? Почему я больше не вижу тебя? Почему не могу вспомнить твое лицо?

Кто свободен от гравитации? Точно не птицы. Просто им лучше удается преодолевать ее, чем нам. Зато рыбы свободны от гравитации. Представьте, если б у вас был плавательный пузырь. Чуть втянули живот, и вот вы уже парите в облаках, пронзаете тучи. Касаетесь вершины горы и взмываете в небо.

Вот так понимаешь, что расстояние между «здесь» и «там» – это ответ на неверный вопрос. А какой же вопрос верный? Давайте подумаем.

Я полагал, что гравитация тянет мои мысли в прошлое, запутывает в воспоминаниях. Но теперь я знаю, что воспоминаниям доверять нельзя. Некоторые из них вымышлены, другие – подправлены. Целая паутина памяти, составляющая мою личность – всё, что я видел и делал, все приобретенные мной умения, – всё это лишь туман.

Гравитация влечет меня в будущее, и на этом пути отпадают какие-то части меня. Все мы исчезаем в тумане возможного. В нашем представлении время – оборотная сторона гравитации.

Увижу ли я тебя вновь в последний миг перед тем, как исчезнуть? Мне хватит лишь мгновения, всего одного взгляда. Это всё, что мне нужно. Моя память дряхлеет, так неужели я больше никогда не увижу тебя, не коснусь твоего лица, не возьму тебя за руку, не увижу себя в отражении твоих глаз? Отчего я, не переставая, плачу? Отчего не могу вздохнуть полной грудью? Всё стало таким мелким и мрачным. Надеюсь, что увижу тебя прежде, чем закончу писать эт…

Я совершенно не знал, что мама больна. Мы с моей женой Джин навестили маму с папой за несколько недель до этого. Утром того дня, когда она умерла, я переписывался с мамой по электронной почте. Вечером, когда они с папой смотрели местные новости, мама попыталась встать с дивана. И не смогла. Попробовала снова и опять не смогла. Папа взял ее за левую руку, но она не сжала его ладонь в ответ. Левая сторона ее лица начала обвисать. Папа сказал: «Я вызову „скорую“». Мама сказала: «Нет, позвони Стиву». – «Какой номер у Стива?» – «Один, два, три, четыре», – и ее не стало. Поздно вечером мне позвонил Стив. Убитые горем, мы поехали в Западную Виргинию на похороны.

Мы не были готовы. В последние десять лет жизни мама почти не менялась. Ее волосы поседели, движения стали медленнее, теперь она лишь сотнями пекла рождественские печенья, чтобы в основном раздать их соседям и родным. Но всё равно она оставалась мамой, милой и умной, и самым большим счастьем для мамы были дни, когда вся семья собиралась у нее дома. И вдруг она исчезла. И папа остался один. Та женщина, с которой он прожил больше шестидесяти лет, больше не будет сидеть напротив него во время обеда, никогда не устроится на диване с газетой, пока он, покачиваясь в своем кресле, смотрит ковбойский фильм. Я больше не увижу мамино имя в ящике электронной почты, не услышу по телефону ее голос, никогда не засижусь допоздна у нее на кухне, то и дело удивляясь ее прозорливости, которой сам я лишен. Всего этого больше нет. Я не был к этому готов, и удар оказался ошеломляющим. Ее нет вот уже десять лет, а рана до сих пор не заживает. И это совсем не то, что простая грусть.

Чтобы еще ярче увидеть разницу между такой скорбью и грустью, одолевающей в дождливый день, давайте на мгновение представим, какими утратами может обернуться дождь, помешавший прогулке. Разумеется, если я не пойду в парк, то буду жалеть обо всём, что связано с этой прогулкой. Позже, когда буду гулять, я увижу другие цветы, иную густоту листвы на деревьях, в парке будут играть другие собаки, другие птицы будут летать в небе. Я буду читать другие страницы или даже другую книгу. За прошедшие дни я получу новый опыт по сравнению с тем, что был бы у меня тогда, пойди я на прогулку. Этот опыт изменил бы мою картину мира и контекст понимания того, что я читаю, того, что я вижу в парке. Но обычно такие изменения малозначительны, и они не сопровождаются чувством утраты. Здесь нет ощущения навсегда закрывшейся двери, а лишь небольшого сдвига в восприятии. И, насколько я могу судить, этот сдвиг не имеет заметных последствий.

Если вы слушали лекции по так называемой теории хаоса, вас, возможно, удивит, что небольшой сдвиг может не иметь заметных последствий. Впервые основополагающие идеи теории хаоса были разработаны Анри Пуанкаре еще в конце XIX века, а затем забыты и несколько раз открыты заново уже в XX веке, пока, наконец, благодаря работе Роберта Мэя по биологии популяций (1976) и книге Джеймса Глика «Хаос. Создание новой науки» (1987) эта тема не вошла в массовую культуру^[54]. Насколько массовую? Она заняла центральное место в новелле «Время и наказание» из эпизода «Маленький домик ужасов на дереве 5» в «Симпсонах». А «Симпсоны» являются важным – быть может, самым главным – барометром современной культуры.

Одна из характеристик хаоса состоит в том, что небольшие изменения могут иметь гигантские последствия, как говорит Абрахам Симпсон: «Если вы путешествуете в прошлое, не наступите там ни на что, ибо даже крохотное изменение может повлиять на будущее так, как вы и представить себе не можете». В математике и точных науках это называется «чувствительностью к начальным условиям». На лекции я начинал с более классического определения, а затем уже давал такую формулировку. Потом я показывал новеллу «Время и наказание». Насколько я мог судить, большинство студентов полагали, что сценаристы «Симпсонов» использовали мое определение чувствительности к начальным условиям, тогда как на самом деле всё было наоборот.

Чувствительность к начальным условиям еще называют «эффектом бабочки». Иногда его объясняют так: «Бабочка взмахивает крыльями в Бостоне, вызывая торнадо в Техасе» (города и страны можете выбрать на свой вкус). Однако чувствительность к начальным условиям означает совсем иное. Мой коллега Дэйв Пик подчеркивает, что крохотной энергии крыла бабочки недостаточно, чтобы самостоятельно вызвать столь мощное явление, как торнадо. На самом деле, об этом говорится в изначальной формулировке Пуанкаре:

Мы видим, что большие пертурбации бывают обыкновенно в тех местах, где атмосфера находится в состоянии неустойчивого равновесия. Метеорологи часто хорошо видят, что равновесие неустойчиво, что образуется циклон, но где именно, они не в состоянии сказать. Лишняя десятая градуса в какой-либо точке – и циклон разражается здесь, а не там; он бушует над странами, которые были бы пощажены, если бы не эта десятая. Если бы мы могли знать эту десятую градуса, то мы могли бы это предсказать; но сеть наблюдений недостаточно густа и сами наблюдения недостаточно точны, а именно поэтому нам и кажется, что всё обусловлено случаем^[55].

Хотя небольшие изменения и не являются причиной больших смещений, однако эти изменения – незаметные в силу нашей неспособности их точно измерить – мешают нам предугадывать, где и когда могут возникнуть большие смещения и могут ли они возникнуть в принципе. Хаос возникает, когда мы не способны предсказать что-либо на сколько-нибудь долгий срок.

Вот почему хаос не может выявить различия между грустью и скорбью. Скорбь не связана с предвосхищением будущего; предвидение (как правило) не предполагает необратимости, поэтому оно (как правило) не является скорбью. В 2002 году моему брату Стиву поставили диагноз ХЛЛ (хронический лимфоцитарный лейкоз). С тех пор он наблюдался в Онкологической больнице им. Артура Джеймса в Колумбусе, штат Огайо. В январе 2010 года Стив упал в обморок – к счастью, тогда он как раз приехал в больницу на томографию. Количество лейкоцитов в его крови в шестьдесят раз превысило допустимую норму, гемоглобин упал на четверть ниже минимального значения, и у него отказали почки. Стива срочно отправили в приемный покой, затем – в реанимацию, где врачи начали делать ему гемодиализ и подключили к аппарату ИВЛ. Пока в «Красном кресте» искали подходящую кровь для переливаний, его кровь выкачивали, пропускали через центрифугу, чтобы очистить от большей части лейкоцитов, восстанавливали с помощью плазмы и возвращали в организм. Стив начал метаться, его движения расходовали кислород, без которого он не мог обойтись, и тогда врачи обездвижили его лекарствами. Они сказали его жене Ким и моей сестре Линде, уже приехавшей в больницу, приготовиться и сделать необходимые звонки. Мы не надеялись, что он доживет до утра.

Всю ночь у меня свербело под кожей. Воспоминания о годах, проведенных со Стивом и Линдой, теснились в моем мозгу так, что до сих пор у меня в голове остались лишь разрозненные, перепутанные и склеенные наугад цепочки, не связанные с тем, как всё было в действительности. Тревога прогнала сон. Всю ночь мы ждали, что позвонит врач и мрачным голосом сообщит – Стив умер. Этот страх причинял боль. Невыносимую боль. И всё же оставалась возможность того, что он выправится и начнет получать какую-нибудь экспериментальную терапию. Та ночь была ужасна, но, насколько мы знали, всё еще было поправимо. И, несмотря на наши опасения, Стив пережил эту ночь, следующий день и еще несколько дней. Примерно через десять дней он вернулся домой. Стив стал участником клинических испытаний, и вот, спустя десять лет, он по-прежнему жив.

В ту ужасную ночь мы не испытывали скорби. Тревогу и страх, граничащий с отчаянием, – да, но не скорбь.

Одним из самых известных повествований о скорби является книга Клайва С. Льюиса «Исследуя скорбь»^[56]. То, что Льюис рассматривает скорбь сквозь призму своей внутренней религиозности, по моему мнению, размывает и одновременно затуманивает впечатление от его реакции на происходящее, поэтому я не стану обсуждать его работу. Вы, конечно, можете придерживаться иного мнения.

Я скажу несколько слов о книгах Джоан Дидион, в которых она подробно излагает свой опыт переживания скорби^[57]. «Год магического мышления» – тонкий и умный рассказ о том, как писательница заново открывала для себя мир, необратимо изменившийся после смерти мужа, Джона Грегори Данна. Дидион сосредотачивается на событиях повседневной жизни, заметно осложнившейся смертельной болезнью ее дочери Кинтаны. Первым делом мне бросилась в глаза сложность задач, которые она ставит перед собой в конце второй главы:

Разумеется, я знала, что Джон мертв. <…> Но сама я вовсе не была готова принять это событие как окончательное. На некоем уровне я верила, что оно обратимо. <…>

Я должна была остаться одна, чтобы он мог вернуться.

Так начался для меня год магического мышления^[58].

В семнадцатой главе Дидион открыто высказывает те идеи, которые весь этот год кипели в ее голове:

Скорбь, оказывается, для любого человека место неведомое, пока туда не попадешь. <…> Мы можем ожидать, что будем потрясены, безутешны, обезумеем от утраты. Мы не ожидаем, что безумие будет вполне буквальным – что «крепкий орешек» будет надеяться на возвращение мужа и беречь его обувь^[59].

Далее она говорит о предвосхищении скорби:

Не можем мы знать заранее (и в этом суть разницы между скорбью, каковой мы ее себе представляем, и скорбью, какова она на самом деле) бесконечного отсутствия, которое наступит потом, пустоты, антисмысла, беспощадной последовательности моментов, когда нам предстоит столкнуться с опытом бессмыслицы – Бессмыслицы с большой буквы^[60].

Поскольку Дидион подробно останавливается на всех деталях своей жизни и рассуждений, замысловатость и глубина ее анализа вызывала во мне медленно закипающее раздражение. Всё, что она рассказывает, казалось мне по большей части банальным, до тех пор, пока мне не перестало так казаться.

Ее книгу «Синие ночи» можно читать как продолжение «Года магического мышления». Это размышления Дидион о смерти дочери, которая ушла через полтора года после смерти мужа. Ее глубокие и трогательные рассуждения об утрате близких и скорби открыли для меня неожиданные стороны восприятия горя.

В качестве беспощадного примера скорби я приведу несколько отрывков из романа Питера Хеллера «Звезды пса»^[61]. Герой-рассказчик Хиг и его пес Джаспер живут в мире, где бо́льшая часть населения вымерла из-за новой респираторной инфекции. (Я начал писать эту главу еще до пандемии COVID-19. Надеюсь, роман Хеллера так и останется фантастикой, однако сейчас, в конце 2020 года, я опасаюсь, что политика американского правительства, противоречащая рекомендациям ученых, может отчасти воплотить эту антиутопию в реальность.) В одну из ночей Джаспер умер. Вот как Хеллер описывает скорбь, охватившую Хига:

Утром я проснулся в окоченении. Спальный мешок и Джаспер были покрыты инеем. Моя шерстяная шапка – тоже.

Ты, наверно, замерз, парень. Иди ко мне. Я натянул стеганое одеяльце с Гринчами, чтобы укрыть его получше. Он был тяжел и бездвижен.

Давай, приятель, всё будет хорошо. Сейчас разведу огонь. Давай.

Он не откликнулся. Я вытащил одеяльце, положил на него пса и слегка коснулся его уха. Моя рука замерла. Его ухо было ледяным. Я провел рукой по его морде, потер ему глаза.

Джаспер, что с тобой? Я тер и растирал. Тер и тормошил его за загривок.

Я подтащил пса, свернувшегося калачиком и окоченевшего, к себе поближе, накрыл его одеяльцем и откинулся на спину. Лежал и дышал. Я должен был заметить. Как тяжело ему было, когда он шел. Слезы, которых не было вчера, хлынули из глаз. Они хлынули, словно прорвав плотину.

Джаспер. Братишка мой. Сердце мое…

Я был опустошен. До предела. Расставание с псом далось мне с огромным трудом. Я пролетел над ним и, казалось, это происходит в какой-то другой жизни. Казалось, что и аэропорт привиделся мне во сне. Но если аэропорт – это сон, значит, и Джаспер – всего лишь сон по ту сторону сна, а до него, еще раньше, был какой-то другой сон. И дальше, и дальше. Все это сны. Так мы мягко превращаем тех, кого потеряли, в прозрачные тени.

Последняя фраза: «Так мы мягко превращаем тех, кого потеряли, в прозрачные тени» – вызывает у меня трепет. Картина скорби погружает нас в жизнь Хига после смерти Джаспера. Это не просто грусть. Утрата останется навсегда, боль неизбывна, хотя в конце цитаты Хеллер замечает, что скорбь может становиться прозрачной. Наконец она превращается в фон нашего повседневного бытия, еще одну ниточку воображаемого полотна жизни.

Если вы думаете, что смерть домашнего животного не способна погрузить вас в пучину скорби, вы, по-видимому, никогда не теряли питомца. Я не стану описывать чувства, которые испытывали мы с моей женой, когда у нас умирала кошка, или чувства моего брата и его жены, когда у них умирала собака. Это описание могло бы занять всю книгу. И все мои слова были бы бесполезны. Я никогда не смогу узнать хоть сколько-нибудь достоверно, что думаете вы, как и вы не сможете узнать, что думаю я. Сопереживание состоит не в том, чтобы знать, что чувствует другой человек, а чтобы представлять, что вы сами почувствовали бы, оказавшись на его месте. Лучшего нам не дано.

Приведу пример. Когда мне было десять, а моему брату Стиву – пять, однажды жарким летним днем папа и дядя Билл взяли нас с собой на песчаный пляж у Нижних Порогов (Лоуэр Фолс) на реке Коул, неподалеку от городка Сент-Олбанс в Западной Виргинии. В то утро на пляже было множество других семейств. Мы со Стивом немного поплавали, держась за надувную камеру от автомобильного колеса. Потом вылезли на берег и стали искать у водопада интересные камешки. Папа и Билл плавали. По воде бродили два брата примерно того же возраста, что мы со Стивом. Но у реки было бурное течение, и младший братишка вдруг исчез под водой. Старший стал звать на помощь. Дядя Билл кинул надувную камеру туда, где исчез мальчуган. Из воды показалась рука, попыталась ухватиться за камеру, но соскользнула и пропала в воде. Взрослые, включая моего отца и дядю, поплыли к тому месту, где исчез ребенок, и стали нырять на дно реки. Мать мальчиков выла и рыдала. Кто-то из взрослых забрался по отвесному берегу наверх, отыскал какой-то дом и вызвал полицию.

Мы со Стивом сидели на песке. Но солнце теперь казалось нам холодным. Старший брат сидел на берегу невдалеке от нас, подтянув колени к груди, обхватив худыми мальчишескими руками худые мальчишеские ноги и уронив на колени голову.

Наконец прибыл патрульный катер полиции. Полицейские начали забрасывать страшные огромные крюки и прочесывать реку. Папа решил, что нам пора уходить.

Я плохо помню, о чем говорили со мной вечером папа и мама, но их слова были тихими, разумными и честными. Это была первая смерть, которую я видел так близко. Смерть тети Рути наступит лишь через два года. В тот раз я впервые увидел нестерпимую скорбь от потери ребенка, от потери брата. Я не мог представить себе, что чувствовал старший брат. Да и как я мог понять? Для этого надо знать так много всего об их жизни. Были ли они друзьями или, наоборот, часто ссорились? Заботился ли старший брат о младшем? Добавлял ли младший в жизнь старшего брата толику милой глупости? Чтобы узнать, что чувствовал старший брат, мне надо было знать ответы на эти и тысячи других вопросов.

Всё, что я мог, – поразмышлять о том, что почувствовал бы сам, если бы умер Стив. Если бы те пять лет, что мы провели вместе, навсегда остались единственным, что между нами было. Если бы Стив стал воспоминанием. Эпизодом прошлого. И ничем больше. Навсегда. Десятилетние мальчики не должны думать об этом темными часами от полуночи до рассвета, а я – думал. Не знаю, что ощущал брат того утонувшего мальчика, но я пытался представить, что чувствовал бы я, если б в тот день утонул Стив. И это был невыносимый, ужасный кошмар.

Нам не дано войти в персональный ад другого, но мы можем представить наш собственный ад, окажись мы в такой ситуации. Только благодаря этому мы можем подумать, сказать и написать что-то путное о скорби. Если нет сопереживания, скорбь остается в нашей голове, как в ловушке. Вернее, у некоторых из нас, чья жизнь – сплошная череда утрат, голова застревает в ловушке скорби.

Итак, скорбь необратима: невозможно скорбеть о том, что обладает некоторой вероятностью, скорбь нельзя испытать заранее. И как бы нам ни было трудно постичь скорбь другого человека, мы понимаем ее сквозь призму сопереживания.

Насчет скорби заранее я бы сделал всё же некоторые исключения. Можно скорбеть о друге, находящемся в терминальной стадии заболевания, или о человеке, который, например, пропал без вести при крушении корабля в море или на войне. Необязательно стоять у гроба, чтобы понять – человек умер или вскоре умрет. И хотя, по-моему, всегда есть шанс, что какое-то новое экспериментальное лекарство совершит чудо или что посреди океана вдруг найдут выжившего, вцепившегося в обломок судна, это всё слишком невероятно, и было бы чересчур жестоко не признавать страдание скорбью, требуя безусловной необратимости факта^[62].

Почему это так, объясню на личном примере. Отец моей жены Джин, Мартин Маатта, умер в 1985 году; ее мать, Банни (Бернис) Маатта, – в 2012-м. Мы приезжали на недельку-две к Банни почти каждое лето (поскольку зима не лучшее время для посещения городка Ишпеминг в штате Мичиган). Лет десять после смерти Мартина мы ездили к Банни и видели ее в полном здравии. Мы целыми днями колесили по Верхнему полуострову, навещали родню. По вечерам Джин раскладывала банковские выписки и счета на полу в гостиной, проверяла, нет ли у Банни просроченных долгов, всё ли сходится. А мы с тещей тем временем засиживались допоздна на кухне, рассказывая друг другу истории из жизни и анекдоты. Например, еще будучи школьницей, Банни подрабатывала в кафе-мороженом «Чоколейт Шоп». В 1930-е годы во многих городах Среднего Запада были бейсбольные команды, которые летом ездили по окрестностям и играли вечерние матчи. Банни рассказывала мне, что в те дни, когда в городе проходил матч, она всегда работала в вечернюю смену. После игры некоторые из спортсменов заходили в «Чоколейт Шоп» попить газировки и съесть мороженое. «Эти парни были потные, мускулистые и красивые», – говорила она. Джин не припомнит этой истории; полагаю, некоторые вещи легче рассказать зятю, чем дочери. Мы с Банни удивительно понимали друг друга. Проводить с ней время было настоящим удовольствием.

Но в какой-то момент мы поняли – с Банни что-то не так. Она стала часто заговариваться, всё время повторять одно и то же, из ее разговоров исчезла какая-то искорка. Джин наняла местных сиделок, чтобы они присматривали за Банни, готовили, убирали, стирали, но главное – чтобы ее не оставляли одну. Это были чудесные женщины; даже теперь, по прошествии стольких лет после смерти Банни, мы навещаем их каждый раз, когда приезжаем в Ишпеминг. Однако в конце концов Банни стала настолько немощна, что этим женщинам было уже не справиться, и Джин отвезла маму в интернат. Там она прожила еще десять лет. Каждое утро она садилась в инвалидное кресло и каталась туда-сюда по длинным коридорам. К тому времени Банни почти не узнавала ни нас, ни других людей, но в целом она была счастлива. Сотрудники интерната любили ее. Вскоре после того, как Банни переехала в интернат, в один из наших приездов Джин решила сфотографировать ее в кресле-каталке. Мы с женой отступили назад, чтобы сделать фото, но Банни смотрела на нас непонимающим взглядом. Несколько сотрудников присоединились к нам и стали махать Банни, чтобы она улыбнулась. Джин попросила меня подойти сбоку и помахать Банни. Я так и сделал. Она посмотрела на меня, оскалилась в язвительной улыбке и показала мне нос. Джин никогда не видела, чтобы Банни так делала. Никогда. Мы все рассмеялись, и Банни тоже, а Джин получила желаемый снимок.

Однако с каждым годом от Банни оставалось всё меньше и меньше. Мы с Джин уже оплакивали то, что, как мы считали, было исчезновением самой «сущности Банни». Доктора говорили, что ее разум угас, а вскоре так же угаснет и ее тело. Мы были раздавлены невыносимым и трансцендентным ощущением утраты, и эта утрата была необратима. То есть это мы так думали.

Когда я навещал Банни, как оказалось, в последний раз, она была очень спокойна, безмятежна. В последний день нашего визита я отвез ее кресло на террасу. Всё это время Банни не выпускала моей руки. Мы втроем смотрели на пруд с рыбками и невысокие деревья, вокруг порхали птицы. Джин стояла слева от Банни, я – справа, и она по-прежнему держала меня за руку. Она никак не реагировала на наши слова. Вдруг Банни повернулась ко мне, нахмурилась, а затем расплылась в прекрасной улыбке и сказала: «Майк». А затем снова пропала. Какая-то ее часть по-прежнему была здесь, рядом. Может, нам надо было чаще разговаривать с ней? Мы не знали. Но ясно было одно: несмотря на то что наступило время глубокой печали, еще не наступило время для скорби.

Очевидной причиной скорби становится смерть. Другие обстоятельства – например, серьезная болезнь или деменция – не столь очевидны. Чем больше мы уверены в том, что утрата необратима, тем ближе мы подходим к тому, что я называю скорбью. В такой момент земля уходит из-под ног. Вам придется самостоятельно заново обрести опору, если вы решите применить описанный мной метод.

* * *

А теперь в нескольких словах расскажу об истории исследования скорби, взяв в качестве основного источника книгу психолога Джона Арчера «Природа скорби» (1999)^[63].

В 1970-х годах психолог Джон Боулби утверждал, что скорбь, как неадекватная адаптация, является реакцией на разлуку^[64]. Как правило, реакции на разлуку бывают адаптивно адекватными, то есть они заставляют нас искать любимого человека, с которым нас разлучили. Обстоятельств, когда подобная реакция приносит пользу, несравнимо больше, чем обстоятельств, когда она бывает во вред, поэтому эволюция не препятствовала развитию данной реакции. Однако скорбь – это реакция на разлуку, возникающая в ситуации, когда воссоединение невозможно.

Психиатр Колин Паркс предположил, что скорбь является неизбежным следствием формирования наших привязанностей^[65]. Боулби и Паркс объясняли, что тревога как реакция на разлуку генетически выработалась в отношении всего, что критически связано с выживанием индивида (маленький ребенок зависит от родителей, которые его защищают и кормят), и с передачей генетического материала потомству (в этом смысле родители зависят от ребенка). Арчер высказывает предположение о том, что с точки зрения эволюции человек лишь недавно научился распознавать смерть, и у нас было недостаточно времени, чтобы выработать разные реакции на разлуку, где воссоединение возможно, и на разлуку необратимую, например смерть.

Арчер описывает исследования, целью которых было свести всё разнообразие реакций скорби к одной переменной. (Вы серьезно? И кому такое могло прийти в голову?) С помощью статистического метода под названием «факторный анализ» (весьма занимательный инструмент, нечто из разряда магии; если вас не пугает статистика и немного математики, поинтересуйтесь этой темой) ученые попытались собрать воедино разнообразные проявления скорби. Результаты оказались не слишком убедительны. Из этого я сделал вывод, что скорбь по сути является высокоразмерным феноменом.

В своем мозгу мы создаем сложные модели тех, кого любим, и эти модели встраиваются в нашу собственную модель, модель самих себя, становясь ее частью. Когда из внешней среды поступают сигналы, что что-то не так – например, что тот, кого мы любим, куда-то пропал, – включается страх разлуки. Мы пытаемся найти соответствие между внешними сигналами и сконструированными ожиданиями. И когда это не получается, нам приходится корректировать свою собственную модель. Это требует времени и определенных усилий.

Первое подробное исследование психологии скорби содержится в «законах горя» Александра Шенда^[66]. За неимением экспериментальных данных, Шенд, для иллюстрации своих идей, обратился к поэзии и литературе. Но даже при наличии экспериментальных данных искусство предоставляет нам примеры живых эмоций более непосредственно, чем любые психологические исследования.

Принято считать, что скорбь имеет несколько стадий или фаз^[67]. Правда, Арчер пишет: «Фазовому подходу очевидно не хватает опытного подтверждения», тем не менее он «представляет собой попытку передать динамический характер процесса скорби». Одно из перечислений этих стадий содержится в одиннадцатом эпизоде второго сезона «Симпсонов» под названием «Одна рыба, две рыбы, рыба-собака, голубая рыба». В японском ресторане Гомер съел суши с ядом рыбы-фугу. В больнице доктор Хибберт осматривает Гомера и заявляет, что тот умрет в течение дня:

Хибберт: По-видимому, вы пройдете через пять стадий. Первая – отрицание.

Гомер: Я вовсе не умираю.

Хибберт: Вторая – злость.

Гомер: Проклятие!

Хибберт: И потом – страх.

Гомер: А что, что после страха?

Хиббберт: Торг.

Гомер: Док, спасите меня, я хорошо заплачу.

Хибберт: И наконец, принятие.

Гомер: Мы все когда-нибудь умрем.

Хибберт: Мистер Симпсон, ваш прогресс удивляет меня.

На самом деле, эти стадии совсем не отражают те чувства, которые испытывает большинство людей. Но, надеюсь, вы согласитесь, что диалог забавный.

Скрытый смысл может придавать словам новые значения. «Исцеление» от скорби подразумевает возвращение к тому, что было до утраты, а это невозможно. Почивший человек по-прежнему мертв. «Перенастройка» означает подгонку нашей модели мира, чтобы включить в нее это отсутствие; при этом мы изменяем все аспекты модели, касающейся того человека, которого больше нет. Жизнь продолжается, но она не станет и не может стать такой же, как прежде. Я не могу смотреть на печенье, не вспоминая при этом маму, которая пекла его по особым случаям к завтраку. Тепло кухни, наполненной ароматом печенья, выбор варенья, процесс накрывания на стол – эти воспоминания вызывали боль на протяжении примерно года после смерти мамы. Теперь те же самые воспоминания вызывают грусть, нежность, и еще более глубокое понимание того, насколько мне повезло быть ребенком Мэри Эрроувуд. Сладкое печенье для меня то же, что для Марселя Пруста пирожное «мадлен». Я не исцелился, но перенастроился.

Один из традиционных методов справиться с тяжелой утратой, так называемая работа горя, состоит из четырех компонентов: принятия того, что утрата реальна; работы над тем, чтобы уменьшить боль утраты; изменения себя, чтобы приспособиться к утрате; и эмоционального отделения себя от человека, который умер. Хотя некоторое время назад гипотеза работы горя была весьма популярна, теперь она встречает определенное сопротивление^[68].

Модель двойного процесса (МДП), созданная Маргарет Штрёбе^[69] и Хенком Шатом^[70], говорит о существовании двух процессов: ориентированного на потерю, когда человек борется со своей скорбью, и ориентированного на восстановление, когда человек раскрывает для себя другие стороны жизни^[71]. Перенастройка подразумевает «колебание» между этими двумя процессами. Это помогает пересмотреть нашу модель мира и модель самих себя. Например, завязывание новых отношений взамен тех, что разрушены смертью близкого, согласно гипотезе работы горя не помогает избавиться от скорби, а согласно модели двойного процесса – помогает. Поможет ли вдове или вдовцу новый брак?

Является ли скорбь результатом эволюции? В книге «Природа скорби» Арчер пишет, что скорбь – это следствие нашей потребности в установлении связей, главной из которых является связь между родителем и ребенком, хотя у социальных животных (в том числе у людей) формируются и другие значимые привязанности. Многие из этих привязанностей важны для выживания, поэтому разрушение связей может представлять угрозу для жизни. Если ребенок разлучен со своими родителями, он оказывается в опасности, поскольку лишен их защиты, кроме того, это ставит под угрозу усилия родителей по передаче своего генетического материала потомству. Важным шагом в развитии теории привязанности является понятие «родственного отбора», предложенное биологом-эволюционистом Уильямом Дональдом Гамильтоном (не путать с математиком Уильямом Роуэном Гамильтоном). Родственный отбор – это эволюционный процесс, благоприятствующий репродуктивному успеху близких сородичей, пусть даже порой в ущерб репродуктивному успеху самой особи^[72]. Гамильтон выводит формулу родственной связи, при которой родственный отбор является эффективным:

степень родства, помноженная на пользу, получаемую родственником, должна превышать ущерб, нанесенный конкретной особи.

Таким образом, привязанность и разлука обладают определенной взаимной симметрией. Гормоны стресса, побуждающие человека к тому, чтобы избегать разлуки и связанных с ней рисков, возникли в результате мутаций, а затем усилились благодаря естественному отбору.

Это справедливо не только в отношении людей: животные тоже могут испытывать страх разлуки и скорбь. У нас во дворе живет уличная кошка, которую мы назвали Пэтч^[73] за серое пятно вокруг правого глаза. Несколько лет назад она родила четырех котят на стройке неподалеку от нашего дома. Рабочие принесли нам котят в коробке, а мы отвезли их в соседний городок, в приют, где животных не усыпляют. Насколько нам известно, привезенных нами котят разобрали по домам четверо работников приюта. Котята были необычайно милые. Всю следующую неделю Пэтч бродила по двору и звала своих детей. В ее криках явно сквозило отчаяние; она почти ничего не ела и только искала котят. Похоже, это был наглядный пример скорби как реакции на разлуку. В конце концов она перестала искать и начала есть более регулярно.

Пэтч часто проводит время в компании Слинки^[74], уличного кота, прозванного так за то, что он крадучись смывается, когда кто-то к нему подходит, а не за его манеру спускаться с лестницы, как предположил мой брат. Мы считаем, что Слинки и Пэтч – брат и сестра из одного помета. Мы с Джин поймали их – сначала одного, потом другого, – чтобы стерилизовать и сделать прививки. Когда один оказывался пойман, другой бродил по клетке и плакал. Едва мы приносили пленника от ветеринара и выпускали его, другой тут же подходил к нему. Они терлись друг о друга головами и уходили парой. Даже теперь, много лет спустя, они неразлучны. По правде говоря, в тот самый момент, когда я пишу эти строки, из окна кабинета мне видно, как они, свернувшись рядом калачиком, лежат у нас во дворе.

Интересно, в тот день, когда Слинки исчез, боялась ли Пэтч, что он не вернется? С моей точки зрения, она вела себя как безумная, совсем как тогда, когда потеряла котят, но я не знаю точно, что творится в голове у кошки. Мне казалось, что оба, Слинки и Пэтч, испытывали скорбь. Но способна ли кошка понимать необратимость? Применимы ли мои критерии скорби ко всем животным?

И всё же вернемся к эволюционной гипотезе возникновения скорби. Разлука активирует гормоны стресса. Сам по себе стресс не обеспечивает выживание, но усилия, направленные на снижение стресса – на то, чтобы найти утраченного партнера, – в случае успеха способствуют выживанию. Однако в ситуации, когда партнер умер, а значит, его нельзя найти, скорбь при всех ее негативных последствиях, похоже, никак не способствует выживанию. Арчер утверждает – дело не в том, что скорбь каким-то образом способствует выживанию, а в том, что это побочный продукт нашей способности чувствовать привязанность, то есть вторичное следствие отбора, в результате которого возник механизм привязанности.

Таким образом, с точки зрения эволюции скорбь – это гормоны стресса от разлуки вкупе с пониманием того, что человек, которого нет, никогда, никогда, НИКОГДА больше не вернется. Очень трудно писать об этом. Время словно сжимается, и множество призраков роится в моей голове. Родители, дедушки, бабушки, тети и дяди, близкие друзья, ученики. (Как ученик может умереть раньше учителя? Когда такое происходит, что-то серьезно ломается в этом мире. Адам, у нас впереди было столько проектов. Какого черта ты курил сигареты? Интересно, что еще нам удалось бы открыть с помощью твоего программирования и моей математики?)А сколько кошек мы потеряли. Никогда больше мой милый маленький Боппер не свернется над моей головой на подушке и не убаюкает своим мурлыканьем.

Мы можем продвинуться дальше в этом направлении, познакомившись с книгой Барбары Кинг «Как животные скорбят», хотя, надо сказать, мне было трудно ее читать^[75]. Для людей, которые любят животных, это эмоционально тяжелая тема. Кинг – талантливый и мощный автор, бо́льшую часть своего материала она подает в виде историй конкретных животных. Такой подход помогает нам понять, что животные способны любить, они способны испытывать скорбь.

Нас ведь не удивляет, что шимпанзе или слоны испытывают скорбь; в конце концов, и те и другие могут пользоваться орудиями и включаться в игру, демонстрируя тем самым достаточно высокий уровень сложности сознания. А по опыту общения со своими питомцами – собаками и кошками – мы много раз убеждались в том, что они способны чувствовать скорбь. А как же дельфины и киты? Черепахи? Курицы, кролики, свиньи, утки, гуси, обезьяны, аисты, воро́ны и во́роны, лошади, козлы, быки? И они все – тоже.

Скорбь у животных основана на чувстве любви. Опираясь на работы Джейн Гудолл^[76], Синтии Мосс^[77], Марка Бекоффа^[78], Питера Фэшинга и других, а также на собственные полевые исследования в Кении, Кинг предлагает такое описание любви у животных:

Когда животное чувствует любовь к другому животному, оно будет из кожи вон лезть, чтобы быть рядом и позитивно взаимодействовать с любимым по причинам, которые не только включают, но и выходят за рамки целей выживания, таких как добыча пищи, защита от хищников, спаривание и размножение.

И:

Если животные не могут больше проводить время вместе (одной из возможных причин этому является смерть одного из партнеров), животное, которое любит, будет открыто выражать признаки страдания. Оно может отказываться от пищи, терять в весе, заболеть, вести себя импульсивно, стать вялым или всем своим видом показывать грусть или подавленность.

То есть Кинг считает способность испытывать скорбь одним из компонентов любви. На самом деле, она называет это достаточным условием для любви. А как же необратимость, которая, по моему мнению, является основным компонентом скорби? Кинг пишет, что «скорбь у животных не обусловлена сознательным представлением о смерти». С каждым примером автор подкрепляет идею о том, будто животные интуитивно чувствуют, что утрата вследствие смерти является окончательной.

Кинг приводит множество случаев, когда после исчезновения брата, сестры или партнера кошки бродят в поисках пропавшего. Часто их поиски сопровождаются жалобным воем, пронзительными криками, причитаниями. Трудно представить, что это еще может так проявляться, кроме скорби.

Известно, что люди скорбят по-разному, иногда другие этого даже не видят. Памятуя об этом, Кинг призывает шире смотреть на то, что мы наблюдаем: «Не стоит требовать от каждой собаки реакции скорби, чтобы поверить в то, что некоторые собаки способны скорбеть».

Животные также скорбят по-разному. Кони водят «лошадиный хоровод» вокруг павшего члена табуна. Подобное же поведение наблюдается и у коров. Что касается слонов, то к умершему члену стада подходят и явным образом оплакивают его не только кровные родичи, но и слоны из других семей.

Издавна существует мнение, что животные, в отличие от людей, живут только в настоящем времени, то есть у них нет понятия ни о прошлом, ни о будущем, а потому чувство необратимости им недоступно. Однако растут свидетельства того, что многие животные обладают эпизодической памятью (особыми воспоминаниями о каком-либо событии, присущими только данному индивиду) и, возможно, автобиографической памятью (воспоминаниями об истории собственной личности)^[79]. Кроме того Кинг описывает шимпанзе Брута, который во время охоты демонстрировал двойное предвидение: он угадывал не только передвижение добычи, но и передвижения остальных шимпанзе в охотничьей стае^[80]. Кинг сделала вывод, что Брут «мог анализировать психическое состояние других шимпанзе», что у него была модель психического состояния сородича.

Идея о том, что человеческому сознанию доступен широкий спектр возможностей восприятия, недоступный животным, по-видимому, подпитывается не столько фактами, сколько людской гордыней. Возможно, нам не стоит безоглядно полагать, что предвидение будущего является исключительно человеческой чертой. Равно как и чувство необратимости, хотя я пока не до конца уверен, к чему в нашем рассуждении следует отнести описанный Кинг феномен, когда некоторые самки обезьян по нескольку дней носят своих умерших детенышей^[81]. Может быть, матери надеются, что их малыши вернутся к жизни? Или они так выражают свою скорбь? У нас гораздо больше вопросов, чем ответов.

Животные могут реагировать на смерть самыми разнообразными способами. Книга Барбары Кинг «Как животные скорбят» откроет вам много нового, только запаситесь носовыми платочками, когда будете ее читать.

А вот другая великолепная книга – «„Я“ значит „ястреб“»^[82] – Хелен Макдональд ставит в центр внимания не скорбь, а ви́дение мира глазами представителя другого вида, ястреба-тетеревятника по имени Мэйбл. Особенно меня очаровали описания того, как Хелен и Мэйбл играют. Играют собаки и кошки, я видел что-то похожее на игру у белок, но не знал, что птицы тоже могут играть. А если это так, то я бы скорее приписал подобное умение воробьям, крапивникам или вьюркам, чем кровавым хищникам. Для меня это стало открытием.

Должно быть, нам даже проще увидеть мир глазами представителя другого вида, нежели глазами другого человека. То, что видит другой человек, всегда проходит через фильтр нашего собственного видения, попадает в контекст наших собственных представлений. Чтобы увидеть мир глазами ястреба, нам надо всё это отбросить. Начать с чистого листа и путем долгого, пристального наблюдения (а это самое трудное, это сотни или даже тысячи часов, проведенных вместе с птицей, часов наблюдений за ее реакциями, совместных занятий) выстроить частичку мира, которая не видна большинству из нас. Прочтите, например:

…я одновременно и ястреб на кустах, и охотник под ними. Такое странное раздвоение заставляет меня чувствовать себя человеком, идущим под самим собой, а иногда и от самого себя. Затем на мгновение всё превращается в пунктирные линии – и я, и фазан, и ястреб. Мы становимся данными в задачке по тригонометрии, где каждый обозначен своей буквой, выписанной изящным курсивом^[83].

«„Я“ значит „ястреб“» – личная история писательницы о том, как жить с ястребом и как его тренировать; но это также история ее скорби об умершем отце. Неудивительно, что она подходит к ней с иной точки зрения.

С тех пор как умер папа, у меня не раз случались такие приступы дереализации, то есть расстройства восприятия окружающего, странные состояния, когда перестаешь узнавать мир^[84].

(В четвертой главе я буду говорить о примерно таком же опыте, который мы испытали с братом. Там было ключевое слово «собака».)

Археология печали всегда в беспорядке. Ты копаешь землю, и лопата вдруг поднимает на поверхность давно забытые вещи. На свет божий извлекается нечто удивительное: не просто воспоминания, но образ мыслей, эмоции, твой прежний взгляд на мир^[85]

Если вы еще не читали эту книгу, прочитайте ее как можно скорее. Что-то вам покажется печальным, что-то – прекрасным.

Врач и ученый Рэндольф Несси опубликовал проникновенное исследование «Эволюционная теория как основа для понимания скорби»^[86]. А совместно с эволюционным биологом Джорджем Уильямсом он написал блестящую книгу «Отчего мы болеем: эволюционная медицина как новая наука»^[87]. Авторы рассматривают болезнь с точки зрения эволюции; их выводы раскрывают нам глаза. Вот краткий пример: обычно немного повышенная температура не причиняет вреда организму, не считая того, что она сжигает немного больше ресурсов. Однако повышение температуры тела даже на пару градусов может существенно замедлить рост патогенов и дает адаптивной иммунной системе время, чтобы идентифицировать атакующие клетки и увеличить выработку соответствующих антител. Сбивать небольшую температуру аспирином крайне вредно. Прочтите эту захватывающую работу тоже. Как видите, я неудержим в своих книжных рекомендациях.

Подход Несси идеальным образом позволяет ему провести тонкий анализ скорби с точки зрения эволюции. Его исследование сосредоточено на следующем вопросе: «Как естественный отбор сформировал механизмы сознания, приводящие к возникновению чувства скорби?» В результате естественного отбора появились процессы, производящие эмоции путем физиологической регуляции. Например, когда наши предки в эпоху плейстоцена замечали вдалеке хищника, они начинали тревожиться, и эта тревожность помогала им ускользнуть от хищника. Отрицательные эмоции могут быть весьма разрушительны, поэтому, если они не способствуют выживанию, то в репродуктивном периоде не выдерживают естественного отбора. Грусть возникает после утраты близкого, и она вызывает у нас несколько ответных реакций: попытаться вернуть утраченное, попытаться предотвратить утраты в будущем, предупредить других о грозящей опасности. Когда утрата необратима и грусть плавно переходит в скорбь, эта разрушительная эмоция может мешать воспроизводству. Однако поступки, совершаемые нами, чтобы подобное не повторилось, способны повысить вероятность выживания потомства.

Не могу не упомянуть вопрос, поставленный Несси: «Является ли скорбь особой разновидностью грусти, предназначенной для того, чтобы справляться с трудностями привыкания к утрате родственника или возлюбленного?» Автор считает, что реальность это доказывает. Однако его подход в основном опровергает эпифеноменологическое толкование, предложенное Арчером. У Несси понятие «грусти» кажется шире, нежели мое.

То, как люди переживают и выражают скорбь, как они подстраиваются, чтобы справиться с утратой, является одной из самых интимных сторон человеческой жизни. В этом нет ничего удивительного: скорбь связана с любовью, а любовь – самое интимное из переживаний. Следовательно, после утраты близкого разные люди ведут себя по-разному.

Моя приятельница, драматург Андреа Слоан Пинк, описала несколько ситуаций, которые случились с ней после смерти матери. Каждый переживает утрату и скорбь у себя внутри. Мы слышим слова скорбящего человека, пытаемся понять его душевную боль, но нам это не удается. Дайте ему высказаться, но не надо утешать. Если можете, предложите ему помощь с повседневными делами. Так друзья часто приносят еду семье, потерявшей близкого человека. В остальном, выслушать – это лучшее, что мы можем. Выслушайте, что говорит Андреа:

Онемение и жгучая боль. Два долгих физических ощущения, вызванные смертью матери, пылали у меня под кожей, а внутри горел нестерпимо яркий свет, более мучительный, чем фонарик офтальмолога. Наконец, эти странные неврологические симптомы ослабли, но я не совсем уверена, что это хорошо. Я не хочу, чтобы кто-то уговаривал меня жить как прежде, снова «радоваться» тому, что не доставляет никакой радости.

Одной из мыслей, поразивших меня после смерти матери, была идея о невероятной расточительности мироздания. Как Вселенная может позволить, чтобы ум, владеющий пятью языками, вдруг в одночасье исчез? Вся накопленная польза, все усилия пускаются на ветер.

Скорбь ослепительным светом озарила всю мою жизнь, высветив ее несуразности. В ней оказалось так много неправильного. Теперь этот свет потускнел, но я помню кое-что из тех уроков, которые бросились мне в глаза.

3. Красота

Украшения в васильковых тонах.

Красота – мостик между скорбью и геометрией. Но чтобы показать это, придется потрудиться.

Барбара Кинг представляет доказательство того, что скорбь связана с любовью. Она сформулировала его для животных:

Скорбь расцветает, потому что два животных привязаны друг к другу, они заботятся друг о друге, может, даже любят друг друга – потому что в душе они уверены, что присутствие другого необходимо, как воздух^[88].

То, что это применимо и к человеку, не требует иных доказательств помимо нашего жизненного опыта. В этой главе мы свяжем скорбь с другим сильным чувством – нашим откликом на красоту.

Выше мы уже связывали геометрию с красотой: некоторые разделы геометрии настолько прекрасны, что у меня захватывает дух. Теперь же я утверждаю, что красота и скорбь – ближайшие соседи, а может даже, скорбь есть мрачное отражение красоты.

В одном это утверждение кажется очевидным: и красота, и скорбь заставляют наши дыхательные пути сжиматься, парализуют диафрагму. Однако от любых сильных переживаний у человека может перехватывать дыхание, так что само по себе удушье не служит связующим звеном между скорбью и красотой. Для этого нам надо заглянуть немного глубже.

О скорби мы уже поговорили и нашли некоторые ее характерные черты, теперь, чтобы обнаружить связь между красотой и скорбью, нам следует раскрыть некоторые свойства красоты. Так же, как мы провели грань между скорбью и грустью, мы должны отделить красоту от красивости. Я начну с воспоминания из своего детства и надеюсь, оно позволит вам провести собственные памятные параллели.

Бывало, что вечерами незадолго до Рождества мы все забирались в машину, и папа вез нас через окрестные села в Сент-Олбанс посмотреть на праздничные украшения. Множество деревьев были обвиты разноцветными гирляндами, вспыхивавшими красными, зелеными, синими и желтыми огнями. Их мама называла «красивенькими». А некоторые были украшены одноцветными – только синими или только белыми огоньками, – их мама называла «красивыми». Я был любопытным ребенком и, конечно, просил маму объяснить, чем отличается «красивое» от «красивенького». К сожалению, я не помню ее ответ, что, впрочем, неудивительно, поскольку дело было в конце 1950-х годов. Мама уже давно умерла, так что теперь у нее не спросишь; но я попытаюсь представить, что она могла мне сказать.

В западной философии учение о прекрасном уходит корнями в Древнюю Грецию и даже глубже^[89]. Наше нехитрое исследование не нуждается во всеобъемлющей теории эстетики. В качестве ориентира я лучше назову трех авторов: Дэниел Берлин, Денис Даттон и Ричард Прам.

В своей книге «Эстетика и психобиология» экспериментальный психолог Дэниел Берлин пишет, что для получения эстетического удовольствия (причем это касается не только красоты, но и красивости) требуются две характеристики: новизна и узнаваемость^[90]. Новизна придает элемент неожиданности. Когда кто-то раз за разом играет гаммы, это не несет новизны; слушать гаммы неинтересно, они не доставляют эстетического наслаждения. С другой стороны, узнаваемость нужна для того, чтобы был некий контекст: если не путь к пониманию композиторского замысла, то хотя бы ориентир, помогающий вместить пьесу в рамки нашего опыта. Радиопомехи не дают эстетического наслаждения, поскольку не обладают распознаваемой формой, в них нет знакомых звуков. Поэтому и красота, и красивость должны проявляться не только как нечто новое, но и как нечто знакомое.

Эта тема впервые появляется в работе Берлина «Теория человеческого любопытства», основанной на его докторской диссертации, которую он защитил в Йельском университете. Берлин заключает, что наибольшее любопытство вызывают объекты со средним уровнем узнаваемости. В основе его исследования лежит представление о конфликте возможных реакций, когда степень любопытства коррелирует со степенью данного конфликта. Слишком незнакомые объекты не дают той реакции, которая способна породить сильный конфликт, тогда как слишком знакомые объекты не порождают конфликт вовсе, поскольку объект ожидаем. Любопытство сильнее всего возникает в наиболее благоприятной зоне между новизной и узнаваемостью.

Теорию Берлина о балансе между новизной и узнаваемостью можно рассматривать как продолжение теории Джорджа Сантаяны о том, что переживание прекрасного вытекает из тонкого баланса между чистотой и разнообразием^[91]. Эта мысль высказана Сантаяной в работе о чувстве прекрасного, посвященной звуку, но он утверждает, что его исследование – «наглядный пример принципиального конфликта, который проявляется повсюду в эстетике». Вот как баланс Берлина описан у Сантаяны:

Поскольку ноту мы слышим лишь тогда, когда в хаосе звука можно различить набор регулярных колебаний, получается, что восприятие и ценность этого эстетического элемента зависит от всех элементов, которые не подчиняются простому закону. Это можно назвать принципом чистоты. Но если бы работал только этот принцип, то самой прекрасной музыкой был бы звук камертона. <…> Принцип чистоты должен сочетаться с другим принципом, который можно назвать принципом интереса. Объект должен обладать достаточной степенью разнообразия и выразительности, чтобы удержать наше внимание и широко взбудоражить нашу натуру.

Сантаяна не упоминается в книге Берлина «Эстетика и психобиология». Это говорит о том, что понятие новизны и узнаваемости (или чистоты и разнообразия) как необходимого условия эстетического восприятия было уже общепринятым, когда Берлин писал свою книгу. Оно просто «витало в воздухе».

Позднее в книге «Инстинкт искусства: красота, удовольствие и эволюция человека» философ Денис Даттон представил теорию эволюционного происхождения понятия о красоте^[92]. Даттон выступает против общепринятой теории о том, что эстетическое чувство культурно обусловлено. Даже минутное размышление показывает, что чувство прекрасного не сводится к нашей культуре. Как, по-вашему, воздушные битвы среди бамбуковых зарослей в фильме «Крадущийся тигр, затаившийся дракон» Энга Ли – это красиво?^[93] Накал и изящество танца Ли Мубая и Цзень Юй; медленно разлетающийся бамбук и молниеносные удары мечей; далекие раскаты грома и виолончель Йо Йо Ма.

Разве на последних страницах романа Жозе Сарамаго «Перебои в смерти» у вас не захватывает дух?^[94] У Сарамаго суть книги никогда не кроется в ее сюжете; главное – фантазия, чувства и особенно язык автора. Роман начинается с фразы: «На следующий день никто не умер». Такое отсутствие смертей продолжается некоторое время, и, хотя вам может показаться, что это благодать, всё оказывается наоборот. Люди по-прежнему болеют и получают увечья; только они не умирают. Возникает множество проблем. Наконец, смерть снова принимается за работу, но теперь люди, привыкшие к отсутствию смерти, жалуются, что не успевают к ней подготовиться. Тогда смерть начинает рассылать в лиловых конвертах письма, где сообщается, что человек умрет ровно через семь дней. Но людям и это не нравится. Однажды одно из писем возвращается обратно. Смерть посылает его вновь и вновь, но оно снова возвращается. Тогда она принимает человеческое обличье и находит того, чьи письма возвращаются ей. Он оказывается виолончелистом. Познакомившись с ним, смерть в конце концов влюбляется, и они спят вместе в его квартире.

Он заснул, а она – нет. И она, смерть, поднялась, открыла сумку, оставленную в гостиной, вытащила письмо в лиловом конверте. Оглянулась по сторонам, будто прикидывая, куда бы его положить – на рояль, между струнами виолончели или же вернуться в спальню и сунуть под подушку, на которой покоилась голова мужчины. Не положила никуда. Вышла на кухню, чиркнула спичкой – это она-то, способная одним взглядом испепелить эту бумажку, обратить ее в неосязаемый прах, воспламенить одним прикосновением пальцев, – и вот обыкновенная спичка, заурядная, жалкая, повседневная спичка подожгла письмо смерти, которое лишь сама смерть и могла уничтожить. И пепла не осталось. Смерть вернулась в постель, обняла спящего и, не понимая, что происходит, ибо смерть не спит никогда, – почувствовала вдруг, как сон мягко смыкает ей веки. На следующий день никто не умер^[95].

В первый раз, когда я читал этот отрывок, меня поразило повторяющееся описание спички, не играющее никакой сюжетной роли. И, хотя, перечитывая этот пассаж позже, я уже не испытывал такого накала, мне открылась вся гениальность замысла Сарамаго. И если вы мне скажете, что этот роман – лишь продолжение одного из эпизодов сериала «Сумеречная зона» начала 1960-х, я пожалею вас за отсутствие воображения.

А как насчет расписных лубочных тканей племен мбути, или анималистической скульптуры инуитов, или наскальных рисунков в пещере Ласко, или мозаик Мескиты (см. наброски на следующей странице)?^[96] Таких примеров множество. Искусство любой культуры может восприниматься людьми любой культуры, так что, если даже восприятие искусства культурно обусловлено, эта обусловленность является незначительной.

Мой отец не был человеком образованным. Он бросил школу и устроился работать на верфях в Ньюпорт-Ньюс, а во время Второй мировой войны, в семнадцать лет, пошел служить на флот. Он был умелым плотником и слесарем, но не очень понимал искусство. Когда на телевизионном экране мелькало изображение какой-нибудь модернистской картины, отец обычно говорил: «Пятилетний ребенок и то мог бы нарисовать лучше». Как-то я показал ему репродукции из книги о Пауле Клее^[97]. Какое-то время он молча их разглядывал, а затем, присвистнув, сказал: «Ну, пожалуй, пятилетний ребенок так бы не нарисовал». И потом он задал вопрос, который несет в себе ключевую проблему понимания красоты: «Как картина может быть такой прекрасной и при этом ничего не изображать?» Перед ним было изображение не какого-либо узнаваемого предмета или знакомой сцены, и всё же оно его зацепило. Отец вырос в Роздейле, в Западной Виргинии, во времена Великой депрессии. Он не любил школу, хотя говорил мне, что ему нравилась математика. Наверное, чтобы меня не обидеть. Во время Второй мировой он служил на Тихом океане. После войны устроился в компанию «Юнион Карбайд» – сначала разнорабочим, затем рабочим силовой станции, потом насосной и, наконец, слесарем в механическом цехе, о чем всегда мечтал. За эти годы он женился на моей маме, и они вырастили троих детей. Сомневаюсь, что он когда-либо переступал порог музея искусств или картинной галереи. И всё же картины Клее вызвали в нем чувства, которые он сам не мог объяснить. Да, восприятие искусства – вещь тонкая.

Эволюционный подход в общем случае основан на отборе, однако Дарвин выделял два главных принципа отбора. Самый известный – естественный отбор, представленный в книге «Происхождение видов»^[98]. Любой признак, увеличивающий вероятность выживания в репродуктивный период, имеет больше шансов передаться потомству, поэтому доля популяции, обладающей этим признаком, растет. Случайные мутации способствуют развитию многих признаков; те, что вредны, отсеиваются естественным отбором. Вот такая простая и элегантная идея. Неудивительно, что люди сразу были ею очарованы.

Второй принцип – половой отбор, предложенный Дарвином во второй книге, «Происхождение человека». В общих чертах, естественный отбор основан на том, что самки выбирают партнеров по определенным признакам, просто потому, что эти признаки кажутся им эстетически привлекательными. Применив теорию Дарвина к восприятию красоты, Даттон пытается объяснить, почему искусство воспринимаемо вне зависимости от культурной принадлежности. «Красота – это природный способ воздействия на расстоянии», – говорит Даттон. То есть восприятие красоты вытекает из удовольствия, получаемого при рассматривании чего-либо, а не при его поедании: разумеется, это лучший выбор, если объектом является ваш партнер или отпрыск. Исследуя глубины нашей истории, философ замечает, что каменные топоры, в изобилии изготовляемые человеком прямоходящим (Homo erectus), которых было избыточно много и большинство из них даже не использовались, похоже, не являлись инструментами для разделки туш. Даттон полагает, что это были предметы самого раннего искусства, «они привлекали не только своей изящной формой, но и искусной выделкой». И тут вступает в действие половой отбор, поскольку умелость является желательным признаком при выборе партнера.

Наконец, орнитолог и эволюционный биолог Ричард Прам выдвигает идею, обратную идее Даттона. В книге «Эволюция красоты» Прам подчеркивает, что изначально концепция Дарвина об осуществлении полового отбора через выбор самкой полового партнера была встречена в штыки: мысль о том, что женщина играет главную роль в выборе партнера, была слишком феминистской для викторианской Англии^[99]. Альфред Уоллес^[100], ярый сторонник дарвиновской теории естественного отбора, был также ярым критиком его теории полового отбора. Уоллес утверждал, что всё можно объяснить одной теорией естественного отбора.

Идея эстетического отбора прошла к своему признанию сложный путь, поэтому мы лишь наметим некоторые этапы. Прам около сорока лет наблюдал за брачными ритуалами птиц, чтобы доказать значимость полового отбора. В одной из лекций об эстетическом отборе для будущих студентов факультета естествознания Йельского университета Прам показывал видеосъемки некоторых ритуалов. Особенно забавным (это можно было бы назвать и более нейтральным словом – «интересным») был танец самца чудной райской птицы. (Посмотрите ролик на «Ютубе»; я не могу подобрать адекватные слова для его описания.) Во время, отведенное для вопросов после лекции, координатор обсуждения, астрофизик Мэг Урри, спросила, почему, посмотрев этот спектакль, самка чудной райской птицы не свалилась со смеху с ветки. Убедительного ответа так и не последовало.

В 1915 году статистик и генетик Рональд Фишер объяснил возникновение половой окраски в ходе эволюции, заметив, что орнаментальная окраска должна была изменяться в соответствии с усредненными предпочтениями^[101]. Но каким образом она эволюционирует? Фишер предложил двухэтапную модель. Изначально орнаментальная окраска указывала на крепкое здоровье или иной признак, реально значимый для выживания. Когда предпочтение (половой отбор), основанное на такой окраске, становится устойчивым (примером может служить всем известный петушиный хвост), орнамент перестает быть признаком выживаемости и выбирается просто потому, что потенциальные партнерши находят его привлекательным.

Последователь и продолжатель идей Уоллеса биолог-эволюционист Амоц Захави в 1975 году предложил принцип «гандикапа», согласно которому окраска – это препятствие для выживаемости, и его существование показывает, что ярко окрашенная особь имеет преимущество перед другими, поскольку сумела выжить, несмотря на такой недостаток^[102]. Многие биологи сочли данный аргумент убедительным. Многие согласны с ним до сих пор.

В 1986 году эволюционный биолог Марк Киркпатрик доказал, что, если неблагоприятный аспект окраски для выживания прямо пропорционален его благоприятствованию для размножения, то ни окраска, ни половое предпочтение не будут развиваться в ходе эволюции^[103]. Следовательно, за счет отбора признак не получит расширения в популяции. Затем в 1990 году еще один эволюционный биолог, Алан Графен, показал, что при нелинейном соотношении между неблагоприятным аспектом яркой окраски и половым предпочтением принцип «гандикапа» может объяснить развитие такой окраски^[104]. Заметьте: «может», но не «должен». Научный спор продолжается.

Накопленные данные Прам интерпретирует в поддержку идеи о том, что окраска и предпочтения коэволюционируют вне действия естественного отбора, то есть и эстетический, и естественный отбор являются двигателями эволюции. Эстетический отбор порождает исторически обусловленные вариации; они каждым элементом зависят от последовательности событий и могут развиваться весьма замысловатыми путями. Фраза Прама «Красота – дело случая» говорит в пользу великого разнообразия форм и кажется неоспоримой, ведь в мире существует около десяти тысяч видов различных птиц. Сложность этих вопросов показывает, как непросто исследовать роль эстетического отбора.

Итак, красота обладает знакомыми и незнакомыми чертами, а эволюция и красота связаны весьма замысловатыми узами. Эволюционный подход поможет нам увидеть, как соотносятся между собой красота и скорбь.

Во-первых, эволюция отчасти проливает свет на различия между красотой и красивостью. Напомню историю про рождественские гирлянды. Красивость – это то, что мы видим на поверхности, а красота затрагивает какие-то трансцендентные глубины сознания. Огни и деревья – настолько разные миры, что само их сочетание подразумевает новизну. (Заметим, что сочетание несвязанных между собой объектов не всегда бывает красивым. Рождественская гирлянда на миске с попкорном вряд ли кому-то покажется красивой.) Узнаваемость исходит из того, что оба предмета являются частью нашей повседневности. Возможно, теория Берлина объясняет тот факт, что разноцветные огоньки вызывают меньший эмоциональный отклик: «…слишком незнакомые модели [обилие разноцветных огней] не вызовут отклика, достаточного для возникновения большого конфликта». Вероятно, это так, но мы лучше посмотрим, что пишет Прам в работе о шалашах, которые строят самцы шалашника. Шалаш – две параллельные стены, сплетенные из веточек (погуглите картинку, это вас впечатлит), возводимые для приманивания самки. Как объясняет Прам: «Самец атласного шалашника собирает предметы для украшения шалаша исключительно василькового цвета и складывает их на соломенной подстилке, располагаемой на участке прямо перед шалашом. <…> В большинстве популяций большого серого шалашника самцы собирают и выставляют напоказ перед своими шалашами светлые камешки, косточки и раковины улиток»^[105]. Эстетический отбор показывает, что композиция из веточек в сочетании с монохромными предметами – это красиво.

Почти наверняка мама объясняла свой эстетический выбор, не руководствуясь брачными ритуалами шалашников. Что бы она подумала, если бы ее десятилетний сын рассказал ей об ухаживаниях птиц? Наверное, она сказала тогда, что красивенькие гирлянды были слишком «суетными», чтобы быть красивыми. Красота должна быть чище и проще. Мир во всей его запутанности и хаосе может быть красивеньким. Мама, конечно, не стала бы использовать слово «трансцендентный», хотя, несомненно, она его знала, поскольку много читала. Но я полагаю, что именно это она пыталась описать: ее собственное понимание того, что отделяет красоту от красивости.

Наша ветвь филогенетического древа отделилась от ветви птиц более трехсот миллионов лет назад. Стоит ли сделать вывод о том, что монохромное ощущение красоты генетически передалось людям и птицам от общего предка? Пока мы не знаем, как работает бо́льшая часть нашего генетического кода, вряд ли идея наследования чувства прекрасного может быть убедительной. Скорее всего, это чувство возникало отдельно и независимо на нескольких эволюционных ветвях. Если вы считаете, что такого не может быть, вспомните, что глаза возникали – отдельно и независимо, – быть может, сорок раз в течение всей истории жизни на планете.

Выработалось ли у других видов восприятие монохромной красоты? Монохромны многие цветы, хотя, конечно, не все. Многие, хотя, разумеется, не все, птицы окрашены лишь в несколько цветов, а в оперении превалирует только один цвет. Например, многие лебеди почти полностью белые, а многие самцы кардиналов почти полностью красные. Похоже, половой отбор приходил к такому решению множество раз. Но почему? По-видимому, в абстрактном перцептивном пространстве оно располагается на локальной вершине, если мы позаимствуем понятие адаптивного ландшафта у генетика Сьюалла Райта^[106]. Для многих видов понятие о красоте является (в настоящий момент) адаптивной доминантой. Но нет ничего фиксированного, поскольку каждый вид развивается на фоне эволюции других видов. Если взглянуть шире, эволюция являет собой коэволюцию: мы эволюционируем все вместе.

Трансцендентность красоты – последняя деталь, необходимая, чтобы понять взаимосвязи между скорбью и красотой, а также между красотой и геометрией. Переживание как скорби, так и прекрасного связано с необычайно сильными эмоциями, которые необратимо меняют наше бытие. Кроме того, в ощущениях скорби и красоты присутствует трансцендентность. Увидеть нечто прекрасное означает заглянуть в некую глубину; скорбеть значит ощущать утрату, от которой мы не сможем оправиться долгие годы, а может, всю жизнь.

Красота геометрии также подразумевает большое эмоциональное напряжение, она необратимо меняет наше восприятие, и она трансцендентна. Ибо мы не видим всю геометрию – только ее частичку, намек, тень чего-то более глубокого. Наши мысли о прекрасном – это зеркало, только с помощью которого и можно увидеть общие черты геометрии и скорби.

Впрочем, довольно пространных рассуждений. Я проиллюстрирую эти связи на примере сюжетов из жизни. Не потому, что я считаю свою жизнь какой-то особенной, а потому, что тонкие понятия порой гораздо эффективнее передаются через конкретные сюжеты, чем через абстрактные слова. А еще я надеюсь, что мои истории из жизни заставят вас вспомнить свои собственные. Вряд ли ваш внутренний мир во всём совпадает с моим. Надеюсь, что из своих воспоминаний вы сделаете иные выводы, нежели я. Но, если мы начнем понимать, насколько у всех разные модели мира, каждый из нас сможет усовершенствовать свою модель.

Геометрия в десятом классе была для меня чем-то удивительным. Все обрывки этой науки, которые я изучал на уроках математики прежде или читал в книгах, сложились в единое целое. Строгость и динамика доказательства теоремы – прекрасна, кристальна и чиста. (Да, признаю, что не все одноклассники считали доказательство теорем таким уж наслаждением; некоторым ребятам оно казалось ужасным занудством. Им я скажу: вы многое потеряли.) А потом возникли вопросы. Древние греки определяли число π как отношение длины окружности к ее диаметру. Но почему это отношение одинаково для всех окружностей? На данный вопрос есть ответ, и весьма элегантный, но для любопытного десятиклассника это была восхитительная загадка. Вечером, сидя за столом в своей комнате и делая домашние задания или читая, я иногда глядел в окно. Небо постепенно темнело, становясь из пурпурного темно-синим и черным, появлялись редкие звезды, и я думал о том, что, может, у некоторых из этих звезд есть планеты, где живут существа, способные созерцать мир. И если бы они представили свой мир в виде абстрактных геометрических форм, это была бы, как мне казалось, та же знакомая мне геометрия. Это ощущение универсальности было потрясающим.

Долгие раздумья, а также несколько весьма интересных бесед с моим учителем привели меня к одному выводу: в геометрии зашифрованы факты, касающиеся устройства пространства и времени. Эти идеи сочетались друг с другом настолько ясно, настолько безупречно. Когда у меня в голове полностью оформилось доказательство, когда я понял, что происходит на каждом его этапе и почему, я впервые почувствовал вкус утонченной радости, выходящей за пределы всякой обыденности.

Вдобавок у меня был учитель геометрии, мистер Гриффит. Еще молодой, но уже лысеющий и беззаветно влюбленный в геометрию. И этой любовью он заразил меня. Понимаете теперь, почему я заболел геометрией, когда мне было пятнадцать? И сейчас, в свои шестьдесят девять, я по-прежнему влюблен в нее, как тогда.

В те годы учителям платили немного: впрочем, с тех пор их положение не слишком изменилось к лучшему, и это возмутительно. Мистер Гриффит по вечерам работал на полставки оператором ЭВМ в Дорожной комиссии штата Западная Виргиния. Он пригласил меня в свой компьютерный центр, и однажды вечером дедушка отвез меня в офис Дорожной комиссии в Чарльстоне. Я запомнил огромный зал, заставленный компьютерами величиной с холодильную установку, бобины с магнитной лентой, мигающие лампочки пультов. Мистер Гриффит объяснил, что это за машины и что они делают. Он рассказал, какие задачи решает компьютер: он моделирует транспортный поток на платной магистрали Западной Виргинии. Это была математика в действии, решение реальной задачи в реальном времени. Я уже имел представление о такого рода работе. В конце концов, орбитальный полет астронавта Джона Гленна состоялся, когда я еще ходил в начальную школу. (В ту пору я не знал, что математик Кэтрин Джонсон, которая внесла большой вклад в расчеты НАСА для запуска и приземления ракеты, за много лет до меня ходила в школу за рекой Канова, напротив моего дома^[107].) Зато теперь я смог пощупать всё наяву: увидеть эти машины, даже потрогать их. Математика стала для меня осязаемой вещью.

Где-то в конце весеннего семестра у нас с мистером Гриффитом состоялся разговор о том, какие эмоции вызывает изучение геометрии. К тому времени мы уже проходили более сложные приемы. Доказательства становились более длинными, более изощренными и – по всем параметрам, какие я только мог себе представить, – более красивыми. Но они уже не доставляли столько радости, как те, что мы изучали в начале осеннего семестра. Мы назвали несколько возможных причин такой перемены, включая то, что длинные доказательства гораздо труднее сразу уложить в голове. Но тут мистер Гриффит немного отклонился от темы и спросил, какое у меня любимое музыкальное произведение. Первое, что мне пришло на ум, был Бранденбургский концерт № 5 Баха. Сколько раз я его слушал? Десятки раз точно. Помню ли я, когда впервые его услышал? Да, конечно, это было в доме моего друга Гари Уинтера. Что я чувствовал, слушая звуки этой музыки? Я никогда не слышал ничего подобного, у меня по спине бежали мурашки, это было так прекрасно. Чувствую ли я то же самое, когда слушаю эту музыку сейчас? Не совсем: я улавливаю больше мелодических вариаций, но тот шок, который случился со мной в самый первый раз, больше не повторялся.

«То-то и оно, – сказал мистер Гриффит. – Первый раз, когда ты слышишь или видишь что-то прекрасное, поражает сильнее всего. Иногда кажется, что твое чувство к чему-то угасает после первого же раза. У тебя есть всего один шанс, чтобы увидеть доказательство теоремы Пифагора в первый раз».

Эта мысль преследовала меня годами и даже усилилась, когда я начал изучать логику, программирование, квантовую механику, общую теорию относительности, дифференциальную топологию, динамические системы и, совсем недавно, математическую биологию. И в каждой из дисциплин был свой «первый раз». Например, когда вы начинаете изучать нумерацию Гёделя, то присваиваете номера переменным и логическим операциям, а затем утверждениям^[108]. Если делать всё аккуратно (а Гёдель был весьма аккуратен), у вас получаются утверждения, отсылающие к их собственным номерам. Так возникает рекурсия, с помощью которой Гёдель доказал свою теорему о неполноте. Сама гениальность идеи, удивление от того, что она работает, может вызвать лишь одну реакцию: «…дрожь бежит по спине, перехватывает горло, и появляется чувство, слабое, как смутное воспоминание, будто падаешь с высоты»^[109]. Проверяя доказательство, всматриваясь в него снова и снова, вы можете обнаружить нюансы, которые не заметили в первый раз, но уже никогда не повторится то абсолютное ощущение трепета перед этой красотой.

Когда я вижу нечто прекрасное, мое первое ощущение всегда окрашено скорбью, поскольку я знаю, что никогда больше не испытаю к этому предмету столь же сильного чувства. Когда я вижу нечто красивенькое, у меня не спирает дыхание, как бывает при первом взгляде на красоту. Впоследствии, когда вы снова видите красивенькую вещь, вы испытываете практически те же приятные чувства. Но вы не ощущаете скорби, потому что ваше первое впечатление можно повторить.

Отчасти скорбь геометрии возникает именно отсюда: первый же взгляд на прекрасную геометрическую конструкцию выстраивает наши мысли таким образом, что вернуть их прежний порядок уже невозможно. Нельзя во второй раз посмотреть на нее, как в первый.

Приведу другой пример такого же толкования скорби, снова обратившись к фрактальной геометрии. Все двадцать лет, что я вел этот курс в Йельском университете, моя первая лекция неизменно была посвящена обзору основного понятия – самоподобия. Еще в первой главе мы сказали, что треугольник Серпинского состоит из трех частей – левой нижней, правой нижней и левой верхней, – как показывает рисунок на следующей странице. Каждая из частей подобна всей фигуре в целом, поэтому она называется самоподобной фигурой. Впоследствии я приведу вам еще массу примеров из мира природы: папоротники, деревья, бассейны рек, береговые линии, горные хребты, облака на Земле, облака на Юпитере, звездные туманности, наши легкие, кровеносная и нервная системы, некоторые стихотворения Уоллеса Стивенса, множество (довольно длинных) музыкальных произведений и так далее и так далее. Тема самоподобия выявляет симметрию – симметрию увеличения, – которая дает ключ к иному пониманию многих форм в природе.

Вторая лекция фокусировала внимание слушателей на нахождении простых правил, по которым генерируются фрактальные изображения. Мы снова начинаем с треугольника Серпинского.

Затем сокращаем его масштаб наполовину и ставим этот уменьшенный треугольник на место левого нижнего треугольника изначальной фигуры. Потом вставляем такой же уменьшенный треугольник на место правого нижнего треугольника нижней фигуры (средний рисунок). И, наконец, снова сокращаем изначальный треугольник наполовину и вставляем на место левого верхнего треугольника (рисунок справа). Применив эти три правила к треугольнику Серпинского, вы получите треугольник Серпинского. На самом деле, треугольник и есть та единственная форма, что осталась неизменной в результате применения данных правил^[110]. Если применить их к любой другой фигуре, у вас не получится та же самая фигура. Попробуйте, например, применить эти три правила к рисунку кота (см. ниже). После первой итерации мы получаем трех котов поменьше. Потом девять котов еще меньше. Если так продолжать, то в конце концов вся эта стая котов превратится в треугольник Серпинского.

И сколько бы раз вы ни повторяли ту же операцию, картинка всё так же будет состоять из множества крохотных котов. Фигурой, возникающей в итоге, всегда будет треугольник Серпинского. Однако сам треугольник будет задан именно последовательностью из нарисованных котов.

Когда я показывал на экране проектора эти рисунки один за другим, все студенты смотрели с изумлением, многие даже открыв рот. Я слышал ахи и даже грубые возгласы. Как это происходит? Им хотелось узнать. Затем мы вводили более общие преобразования, комбинировали поворот и отражение со смещением и масштабированием. Когда вы уже набили руку, то запросто находите правила для построения и более сложных фракталов, вроде того, который показан на следующей странице. Тем не менее каждый год с десяток студентов говорили мне, что умение находить правила мешало им получать удовольствие от самих фигур. Стоило научиться раскладывать фракталы на составляющие, и фигуры отчасти утрачивали свою красоту.

Необратимость здесь налицо, но можно ли назвать это скорбью? Мои студенты точно бы так не сказали. Если они и описывали свои чувства, то обычно говорили, что им грустно; некоторые заявляли, что испытывают досаду от того, что прежнее ощущение тайны сменилось стремлением найти отражения, повороты и смещения. Эти прекрасные фракталы превратились в геометрические задачки. Скорбь тут ни при чем.

Для скорби нужна не просто необратимость. Скорбь – это необратимость вкупе с эмоциональным переживанием утраты и трансцендентностью. Если утрата не имеет для вас огромного значения, вы не почувствуете никакой скорби. Немногие из моих студентов (если таковые вообще есть) считают геометрию одной из важнейших сторон своей жизни.

Но для меня она именно такова. Каждый раз, когда я узнаю еще один небольшой кусочек геометрии, каждый раз, когда в пространстве моего восприятия открывается новая дверь, остальные двери тут же закрываются. Постепенно я осознал, что каждая из этих закрытых дверей навсегда отрезает меня от целого мира возможностей; я не могу взглянуть на новую задачу взглядом, не замутненным уже имеющимися у меня знаниями. Мой взгляд не может быть иным: каждый шаг в познании геометрии, конечно, позволяет мне увидеть связи, которые иначе я никогда не увидел бы, однако он же не позволяет мне увидеть те связи, которые я бы увидел, не имея этого знания. И я действительно скорблю об утрате этих возможных миров. Конечно, не так, как я скорбел об утрате родных или о моих умерших котах, и всё же чувство утраты меня гложет, оно свербит, и утрата эта необратима.

Если вы не помешаны геометрии, как я, вам подобные доводы могут показаться смехотворными. И для вас они именно таковы. Но моя цель – помочь вам найти нечто подобное в своей жизни. Размышление о потенциальной потере, о потенциальной скорби может помочь вам лучше понять, как разобраться с реальной скорбью в реальной ситуации. Приведу пример.

Многие годы я заканчивал свой курс фрактальной геометрии рассказом о Генри Гурвице. В начале 1990-х я преподавал в Юнион-колледже в Скенектади, штат Нью-Йорк. Там я разработал лекции по математике во фрактальной геометрии и в теории хаотических динамических систем для студентов младших и средних курсов. Дэйв Пик с физического факультета придумал похожий цикл лекций, но с меньшим упором на математику, чтобы познакомить студентов-гуманитариев с квантитативным мышлением. Его курс мы обдумали и разработали вместе. Позднее, когда мы оба покинули Юнион-колледж, я перенес свои лекции в Йельский университет, а Дэйв – в Университет штата Юта. Мы развивали свои курсы независимо друг от друга, но корни у них были общие. Годы, когда мы с Дэйвом работали вместе, были одними из самых счастливых в моей жизни. Интересно, как бы сложилась жизнь, если бы мы остались в Юнион-колледже и еще лет двадцать проработали вместе. Я скорблю об этой потере. Очень.

Разумеется, самым известным преподавателем в Юнион-колледже был Ральф Алфер. Ученик Георгия Гамова, Ральф провел несколько оригинальных вычислений, превративших модель Большого взрыва из завораживающей картинки в основательную космологическую теорию с проверяемыми расчетами. Ральф сначала работал в исследовательской лаборатории «Дженерал Электрик» в Скенектади и в конце концов стал преподавать в Юнион-колледже.

Генри Гурвиц был физиком-ядерщиком в «Дженерал Электрик», где и познакомился с Ральфом. Уйдя на пенсию, Генри понял, что ядерная физика – это не хобби, которым можно продолжать заниматься дома, поэтому он купил персональный компьютер IBM и начал подыскивать задачи, требующие решения. В предустановленном пакете была программа, которая генерирует изображение множества Мандельброта, показанного на следующей странице^[111]. А не взяться ли ему за какую-нибудь задачу, связанную с множеством Мандельброта? Генри спросил у Ральфа, а Ральф отослал Генри ко мне. С множеством Мандельброта связано несколько очень хитрых задач, и одна из них до сих пор остается нерешенной, несмотря на годы усиленного труда гениальных математиков. Но мне была известна другая задача: вывести доказательство закономерности, зафиксированной в числовом выражении моим студентом Адамом Робуччи (которого я упоминал на с. 99). Генри заинтересовался этой задачей и в течение пары месяцев регулярно появлялся у меня в кабинете. Особенно меня радовало, что к нашим дискуссиям присоединился Дэйв Пик. Каждую неделю Генри сообщал, что сделал за последнее время. Мы закидывали его вопросами, предлагали варианты, и Генри возвращался домой. В течение недели мы с Дэйвом обсуждали задачу в его кабинете, в моем кабинете и в коридорах между нашими кабинетами. Это было здорово.

Однажды Ральф пришел ко мне и спросил, как продвигается работа у Генри. Я сказал, что он достиг больших успехов, но пока не нашел ключевой идеи. Ральф спросил, можем ли мы немного ускориться.

– Почему мы должны ускориться?

– Потому что у Генри обнаружили рак в терминальной стадии. Ему осталось жить всего несколько месяцев.

– Это ужасно. И что он будет делать?

– По дороге от врача домой Генри купил более быстрый компьютер.

Черт возьми. Только теперь я понял, насколько Генри любил решать задачи. Мы с Дэйвом стали прилагать еще больше усилий. Генри по-прежнему приходил ко мне каждую неделю. Он не говорил о своей болезни, поэтому и мы о ней не упоминали. И кусочки решения задачи начали вставать на свои места.

Когда Ральф снова заглянул ко мне в кабинет и спросил по поводу проекта, я сказал ему, что мы очертили основные идеи доказательства. Оставалось несколько деталей, но я был уверен, что мы с этим справимся. Ральф сказал, что Генри не протянет до следующей недели. Дети приехали к Генри и его жене, чтобы побыть с ними в последние дни жизни отца. Для Генри было важно знать, что мы с Дэйвом завершим наш общий проект. Должен ли я ему это сказать? Конечно, да.

Ральф ушел, а я подумал: «Как же я ему теперь скажу?» Я встречался с Генри только в своем кабинете. Я не мог просто прийти к нему домой и, когда его жена откроет дверь, сказать: «Мне очень жаль, что Генри скоро умрет, но я пришел поговорить с ним о математике». Примерно по той же причине и звонить было неудобно. В то время еще не все пользовались электронной почтой, да и в любом случае это было бы слишком безлико. И я написал письмо. Я написал Генри, как нам с Дэйвом нравилось работать с ним, и пообещал, что мы доведем решение задачи до конца. (И мы сделали это.)^[112] Я отправил письмо во вторник. А в следующий понедельник мне позвонила вдова Генри. Он получил письмо в четверг, прочел его, подумал немного и заявил, что не верит, будто нам с Дэйвом удастся найти решение. Он перестал принимать обезболивающие и продолжил работать над задачей, набрасывая контур всех недостающих шагов. Вдова Генри сказала, что в последние дни он находился в своей лучшей форме, он работал над задачей. Делал то, что любил больше всего на свете. Не хочу ли я выступить на его вечере памяти?

Я вышел на сцену вместе с Ральфом и Айваром Джайевером, нобелевским лауреатом из Политехнического института Ренсселера, также работавшим с Генри в «Дженерал Электрик». То, что я сказал тогда на вечере памяти и повторял потом в конце своего курса, звучало так: «Я многому научился у Генри, но главное, что я понял, наблюдая, как Генри работает: надо заниматься тем, что любишь. Если ты всю жизнь проводишь на ненавистной работе, только чтобы заработать кучу денег, ты просто генетический мусор. Генри любил решать задачи. Я люблю преподавать. Истинная цель обучения в том, чтобы перепробовать множество областей знаний и найти то, что тебе действительно по душе».

Когда в конце концов я стал преподавателем, я не мог дать студентам иного совета, чем просто наблюдать за собой, чтобы найти то, что любишь: я понятия не имел, как это сделать. Теперь я это знаю. Представьте, что вас навсегда отлучили от работы в вашей области. Будете ли вы горевать? Не просто грустить, а по-настоящему скорбеть? Вот так можно узнать, любите ли вы свое дело.

Весной 2016 года я оставил преподавание. Здоровье уже не позволяло мне вести занятия на высоком уровне, которого заслуживали мои студенты, и вместо того, чтобы делать свою работу вполсилы, я ушел. Для меня это был даже не удар бейсбольной битой по голове, а удар кувалдой. Я скорбел. И по-прежнему скорблю.

И всё же, когда в очередной раз я чувствовал скорбную горечь, проснувшись ото сна, в котором снова стоял на кафедре учебной аудитории, это лишь доказывало, что я провел сорок два года своей жизни, занимаясь любимым делом. Пусть моя работа была незначительна, но это то, чем мне следовало заниматься. Геометрия, преподавание и коты. Преподавать я больше не могу, и геометрия с каждым днем выветривается из моей головы. Одна дверь уже навсегда закрыта, другая тоже начинает закрываться. И каждый день я плачу о них. Но мы с моей женой по-прежнему можем наслаждаться весенними зорями и осенними вечерами. Мы все так же можем заботиться о своих котах и наслаждаться их компанией.

Скорбь о геометрии понятна в основном геометрам, хотя, надеюсь, моя история поможет вам увидеть в своей жизни те области, которые так же важны для вас, как геометрия для меня.

Впрочем, в следующей главе я надеюсь убедить вас в том, что геометрия скорби имеет отношение к каждому.

4. Повествование

Тень изломанной тропинки.

Каждый из нас переживает скорбь по-своему, она скроена по нашей мерке и занесена в скрижали исключительно для наших глаз. Тем не менее я утверждаю, что геометрия может помочь нам понять свою собственную манеру скорбеть. Это не пошаговая схема, а совокупность тропок или путей, идущих через абстрактное пространство. Сначала мы увидим, как это происходит, а затем разберем, почему.

Абстрактное пространство – не только пространство эмоции. И не только бесконечно разветвляющиеся временны́е пути, о которых говорится в рассказе Хорхе Луиса Борхеса «Сад расходящихся тропок», где каждый сделанный нами выбор вел лишь по одной из всех возможных ветвей будущей жизни^[113]. Пространство, которое я называю пространством повествования (story space), чрезвычайно многомерно, быть может, у него бесконечное количество измерений. В нем есть отдельное измерение для каждого независимого компонента мироздания, способного повлиять на вашу жизнь. Казалось бы, слишком общие слова: вряд ли они нам помогут. Никто, даже самый бдительный морпех, не может отследить всё, что творится вокруг него. Благодаря пространству повествования меняется наш фокус восприятия. В каждый момент мы способны осознавать, наверное, меньше десятка аспектов внутри и вокруг нас, которые влияют на наши действия. Но с течением времени и по мере изменения ситуации меняются и аспекты – измерения, имеющие большое значение. Наш путь через пространство повествования – расплывчатая траектория, ограниченная подпространством малой размерности этого пространства. Но и подпространство, и его измерения меняют течение нашей жизни.

Идея пространства повествования несколько десятилетий вытанцовывалась где-то на периферии моих размышлений и часто всплывала в качестве побочной темы, когда мы с поэтессой и журналисткой Амелией Урри обсуждали примеры фракталов в литературе для четвертой главы «Фрактальных миров».

Мы будем использовать модель пространства повествования «жизнь как путь», хотя возможны и другие варианты. В одном из них время не является независимой переменной: наши воспоминания и фантазии переносят нас назад и вперед во времени, давая некоторое повествовательное выражение представлению о том, что время – некое стихийно возникающее явление. Мы помним прошлое, но не будущее, потому что для воспоминания требуется собрать воедино данные, полученные извне; мы не способны воспринять и обработать достаточно деталей, чтобы вспомнить будущее. Это весьма хитроумная идея, отлично изложенная в замечательных книгах физика Карло Ровелли^[114].

Некоторые писатели разрабатывали иные геометрические модели сюжетов. Забавный пример представляет «Урок литературного творчества» Курта Воннегута^[115]. Джон Макфи^[116] дает любопытный очерк сходства между структурой повествования и географическим рельефом^[117]. Как ни крути, но нас повсюду окружает геометрия. Она влияет на наше восприятие и упорядочивает мысли, создавая многочисленные категории. Геометрия может помочь нам найти связи, которых мы раньше не замечали.

В каких измерениях может существовать пространство повествования? В каждом конкретном случае мы сосредоточимся лишь на нескольких аспектах, но давайте начнем с более широкого перечисления. Перечислим несколько возможных измерений пространства повествования:

• физическое положение;

• эмоциональное состояние;

• физическое окружение;

• люди вокруг;

• текущее содержимое вашей краткосрочной памяти;

• задачи, которые вы видите перед собой;

• пространство действий (событийные сценарии).

Это лишь общие категории: каждую из них можно подразделить на более независимые координаты. Например, эмоциональное состояние можно описать точкой на оси страх-безмятежность. И, независимо от нее, точкой на оси спокойствие-гнев. А еще существует много других осей. Они независимы друг от друга, поскольку чувство страха или расслабленности никак не влияет на ваше чувство спокойствия или гнева.

Серьезно? Можно ли одновременно быть безмятежным и рассерженным? По своему личному опыту, твердо скажу: да. Я учился в седьмом классе. Школа была примерно в трех километрах от дома, я любил ходить туда пешком. Однажды, возвращаясь пешком после занятий, я увидел, как какой-то девятиклассник (ростом гораздо выше меня) вытаскивает из кустов кота и достает из кармана баллон со светящейся краской. Не успел он открыть крышку баллона, как я бросился вперед и всей массой тела ударил его под колени. Кот, невредимый, удрал прочь, а я хорошенько навалял тому парню. Я вовсе не горжусь ни своим поступком, ни своими чувствами по этому поводу, но я на самом деле одновременно ощутил тогда и гнев на этого парня, и безмятежное удовлетворение от того, что спас кота. Не могу подробнее разобрать свои тогдашние чувства, скрытые за завесой шести десятков лет.

Кроме того, эмоциональное состояние подразумевает наличие точки на оси грустный-радостный и на многих других осях, какие только может создать наша фантазия. Я читал, что у нас существует восемь основных эмоциональных состояний; другой источник называет десять, третий – двадцать. Остановимся на том, что их «много». Глядя на разные перечни состояний, вы заметите, что они включают в себя разные наборы эмоций. Если вас это сбивает с толку, скажем просто: сложные эмоциональные состояния можно разложить на составляющие различными способами.

Приведем рисунок, чтобы нагляднее проиллюстрировать такую декомпозицию, представляемую нами в виде точки на различных системах координат.

Слева мы видим, что положение каждой точки на плоскости определяется расстоянием по оси x (жирная черточка на оси x) и расстоянием по оси y (толстая штрихованная линия на оси y). Справа мы видим, что та же самая точка может быть определена расстоянием по оси u (жирная черточка на оси u) и расстоянием по оси v (толстая штрихованная линия на оси v). То же самое можно сделать для любой пары осей u и v при условии, что они не параллельны.

В качестве физического примера я могу описать свое (приблизительное) местоположение в терминах широты и долготы, или просто указав свой адрес. И то и другое дает примерно одну и ту же информацию, однако используются совершенно разные системы координат.

Аналогичные построения можно произвести и в более многомерных пространствах, но нарисовать их будет немного сложнее. Чтобы получить об этом более широкое представление, правильнее обратиться к разделу математики под названием «линейная алгебра».

Полезным замечанием, которое мы назовем принципом ограниченного внимания, будет то, что в каждый конкретный момент мы имеем доступ лишь к нескольким координатам нашей точки в пространстве повествования. Наше точное местоположение всегда определенно, но мы сознательно принимаем во внимание только проекцию, или тень, этой точки в подпространстве, очерченном небольшим количеством координат. Что такое подпространство? Это то, что получается, если не принимать во внимание некоторые из координат. Например, плоскость x-y – это подпространство трехмерного пространства.

Представленный нами краткий перечень измерений – лишь начало. Разберем его на незначительном (даже пустячковом) примере. На протяжении долгого пути по лесу Билл и Стив ощущают себя довольно безмятежно: Стив в большей степени, чем Билл. Билл слышит шум: возможно, это медведь, – поэтому Биллу становится тревожнее. Но вскоре он видит, что шум вызван оленем; тревога рассеивается, и Билл снова безмятежно идет по лесу, хотя и менее беззаботно, чем до того, как он услышал шум. В конце концов, в следующий раз это может быть и медведь. (См. рисунок на следующей странице.)

Стив не так хорошо знает лес, поэтому он обращает внимание на шум (то есть обрабатывает его) несколько позже, чем Билл. Следовательно, тревожность Стива начинает возрастать позднее и достигает более высокого пика, нежели тревожность Билла. Поскольку Стив также замечает оленя позже, чем Билл, его тревога всё еще растет, в то время как у Билла она уже снижается. В конце концов, тревожность Стива снижается, но какое-то время после встречи с оленем она балансирует на грани.

На двумерной схеме, где горизонтальная ось – это время, а вертикальная – ось тревожность-безмятежность, мы видим, что линии Билла и Стива пересекаются в одной точке. Как показано на нашем простом чертеже, в какой-то момент психическое состояние у Билла и Стива одинаковое.

Теперь добавим другое измерение, ось спокойствие-гнев. Предположим, что в период переживания тревоги по поводу медведя Стив находится в нулевой точке данной оси. То есть его линия остается в плоскости, обозначенной осями тревожность-безмятежность и время. Пересечения кривых и прямых линий помогут нам вычленить третье измерение, изображенное на рисунке.

Давайте предположим, что Билл вначале несколько рассержен: наверно, потому, что Стив выкинул значительную часть их запасов. (Если это кажется вам абсурдом, почитайте забавную книгу Билла Брайсона «Прогулка по лесам», из которой я взял этот пример^[118].)

Надписи на рисунках:

Тревожность, Билл, Стив, время, безмятежность.

Тревожность, гнев, спокойствие, время, безмятежность.

С течением времени гнев Билла уменьшается, но всё же он еще немного сердится. Как мы видим на нижнем рисунке, душевное состояние Билла, развивающееся в трех измерениях, никогда не совпадает с состоянием Стива.

Этот простой пример показывает: добавляя измерения, мы можем увидеть, что линии, которые, казалось бы, пересекаются, на самом деле не пересекаются. И наоборот, убирая измерения (то есть проецируя, рассматривая тень), мы можем сделать так, что непересекающиеся линии будут казаться пересекающимися. Слово «казаться» не совсем правильное: в том подпространстве, на которое они проецируются, данные линии действительно пересекаются.

Почему для нас это важно? Я собираюсь доказать, что в пространстве повествования скорбь являет собой разрыв, скачок, слом траектории. Затем, если мы спроецируем две части разорванной траектории правильным образом, то тени этих частей сойдутся. То есть в этом мире теней скорбь исчезнет.

Может ли это сработать? Может ли геометрия действительно остудить раскаленную добела скорбь необратимой утраты?

Начнем с соотношения между скорбью и разрывом траектории. На уроках школьной алгебры мы научились отличать прерывистые линии от непрерывных. Здесь нам не нужны математические определения, достаточно одной интуиции. Траектория непрерывна, если можно начертить ее график, не отрывая карандаш от бумаги. Если карандаш приходится отрывать от бумаги, то скачок между одной частью кривой к другой части будет являться разрывом.

Отчего в пространстве повествования возникают прерывистые траектории? Скорбь – это выражение необратимой потери. Чтобы проиллюстрировать, как она отображается в геометрии пространства повествования, я приведу в пример смерть моей матери. Пространство повествования, описывающее меня и мою семью, разделено на несвязанные друг с другом подпространства, «мир, где есть мама» и «мир без мамы». Когда мама умерла, траектории каждого члена моей семьи перескочили из подпространства «мир, где есть мама» в подпространство «мир без мамы». (Если вы знакомы с подпространствами из линейной алгебры, вы увидите, что здесь я допускаю некоторые вольности. Считайте, что я использую термин «подпространство» метафорически, или просто замените термин «подпространство» на «подмногообразие».) Теперь касательно данной конструкции стоит отметить два момента:

Скачок от «мира, где есть мама» к «миру без мамы» необратим. Ни одна жизненная траектория не совершает обратный скачок: от «мира без мамы» к «миру, где есть мама».

Пространство повествования каждого человека содержит невероятное количество разрывов. Но лишь те разрывы, которые связаны с большим эмоциональным всплеском, становятся важными составляющими нашей индивидуальной жизненной траектории.

Надписи на рисунке:

Страдание; мир, где есть мама; мир без мамы; время; все остальные координаты

Является ли скорбь единственной причиной разрывов? Или любая необратимость должна выражаться в прерывистости? Как насчет необратимости, возникающей, когда вы в первый раз посмотрели фильм «Будучи там» с Питером Селлерсом^[119]? Невозможно пережить заново удивление от финальной сцены. По правде говоря, каждый раз, когда вы будете смотреть любой другой фильм с участием Питера Селлерса, вы будете видеть садовника Чэнса, идущего по воде, а затем погружающего в воду зонтик по самую рукоятку под нарастающие звуки музыки и распевный голос Джека Уордена: «Жизнь – это состояние души». На соответствующей оси – например, на оси «Является ли садовник Чэнс богом?» – этот момент может обозначать разрыв. Но действительно ли данная ось играет большую роль в вашей жизни, в вашем образе мыслей? Очевидно, гораздо меньшую, чем ось «мама жива?». Для скорби необходим разрыв по оси, несущей большую эмоциональную нагрузку.

А что, если не учитывать ось времени? Можно ли найти разрывы, меняя положение вдоль оси, которая представляет что-то кроме времени? Это интересный вопрос. Дам вам немного поразмышлять над ним. Геометрия пространства повествования предлагает массу возможностей для исследования.

Мы закончим эту главу простым примером того, как знакомство с пространством повествования помогает снизить накал скорби. Прежде чем мы перейдем к примеру, я должен подчеркнуть, что я не могу и не стану давать никаких общих советов о том, как уменьшить боль утраты. Я приведу вам пример, но сможете ли вы уменьшить свою боль и как вы это сделаете, зависит от тонких градаций той значимости, какую вы придаете осям вашего пространства повествования.

Я не буду приводить в качестве примера смерть кого-то из моих родственников, а лучше расскажу о смерти нашего самого первого кота, потрепанного бродяжки, которого Джин назвала Скраффи. У нашего соседа в Скенектади были свои коты, и он подкармливал еще и уличных, поэтому коты часто приходили к нам во двор. Джин любила котов. Я тоже, но у меня была на них ужасная аллергия. У нас во дворе стал подолгу задерживаться один маленький черный котик. Он ждал, пока Джин вернется со своей работы в медцентре Олбани, подбегал к ней и терся о ее ноги. Джин ласкала Скраффи, а когда она садилась на скамейку у нас на заднем дворе, Скраффи запрыгивал к ней на колени и засыпал, свернувшись калачиком. Так прошло несколько недель, и Джин отнесла Скраффи к ветеринару, чтобы сделать прививки. Я остался работать дома. Через полчаса Джин позвонила мне вся в слезах и сказала, что у Скраффи обнаружили кошачий лейкоз. Хотя от него есть вакцина, после заражения болезнь уже неизлечима, смертельна и невероятно заразна. Скраффи надо было усыплять. Не хочу ли я прийти в клинику, чтобы попрощаться с ним? «Не то чтобы хочу, но по твоему голосу я чувствую, тебе нужна поддержка. Через пару минут приду», – ответил я.

Ветеринарная клиника находилась в пяти кварталах от нашего дома. Я зашагал туда. И тут подумал: «Скраффи такой милый котик, такой ласковый и дружелюбный. Почему бы нам не поселить его внизу? Я мог бы переехать наверх. Да, так и сделаем». Потом я задумался: «А как усыпляют кошек? Наверное, ветеринар делает укол. А что, если он уже готовит шприц?» И я побежал. За всю свою жизнь я, наверное, не пробежал и мили. А тут побежал. И вот я уже в клинике. Где Джин? В первом кабинете. Бегом в первый кабинет. Джин держит на руках Скраффи, а врач готовит шприцы. (Нужно два укола.) Я говорю – гораздо громче, чем обычно: «Стойте, стойте! Пусть Скраффи живет у нас внизу». «А как же твоя аллергия?» – спрашивает Джин. «К черту аллергию! – снова слишком громко говорю я. – Мы не станем убивать кота из-за какой-то моей аллергии». «Вы очень добры, – говорит ветеринар. – Но Скраффи осталось жить всего полгода». «Неважно. Мы будем заботиться о нем до конца его жизни».

И Скраффи переехал к нам в полуподвал, а я полгода не заходил туда, постоянно мыл руки и бесконечно пил антигистаминные. Через полгода мы стали днем выпускать Скраффи побегать по дому, а на ночь уносили вниз. И снова мытье рук, снова антигистаминные. Через год после того, как взяли кота к себе, мы разрешили ему бегать по дому всё время. В первую же ночь, оказавшись вне полуподвала, Скраффи запрыгнул на кровать, зарылся под одеяло и свернулся калачиком у Джин на плече. И так он спал с ней на протяжении почти шести лет. Любовь не может остановить болезнь, но может значительно замедлить ее развитие.

Мы поняли, когда для Скраффи наступили последние дни. Кошачий лейкоз спровоцировал настоящий лейкоз. И я, и Джин уже теряли родных из-за этой болезни, поэтому мы были знакомы с общей эмоциональной механикой, сопровождающей осознание того, что до конца осталось совсем немного. Но опыт не притупил боль этого ожидания. Необратимость поразила меня уже тогда, почти двадцать лет назад. Скраффи умрет и никогда уже не возродится, а я ничего не могу с этим поделать.

Мы отвезли кота к ветеринару. Тот сделал первый, успокоительный, укол, а потом оставил нас наедине, чтобы мы попрощались со Скраффи. Он сидел на столе. Мы ласкали его и разговаривали с ним. Он мурлыкал и смотрел на нас. Затем передние лапы перестали его держать. Мы позвали ветеринара. Он сделал второй укол, и Скраффи не стало. Мир наполнился тьмой и слезами.

С тех пор мы подобрали много уличных котов. На сегодняшний день мы уже потеряли Крамплс, Динки, Чесси, Дасти, Боппера, Лео и Фаззи. Все они умерли в местной ветеринарной клинике, все от рака, и каждый раз их смерть разбивала нам сердце. Я не знаю ничего, абсолютно ничего на свете, что могло бы как-то облегчить или пустить в иное русло ту мгновенную боль, возникающую в ответ на необратимый переход от «Боппер жив» к «Боппер мертв». На мгновение вы оказываетесь в свободном падении. Земля уходит из-под ног, и вы летите вниз. От этих первых мгновений невыносимой скорби никуда не деться. Но, начиная со Скраффи, я нашел способ уменьшить остаточную боль, когда пройдут эти самые первые мгновения.

Нам не нужно избавляться от боли совсем, ведь переживание скорби очень интимным и сложным образом связано с сопереживанием другому. Я пишу эти строки весной 2020 года, глядя, как главы исполнительной власти американского правительства совершают ошибку за ошибкой в своих изначально неверных потугах «обуздать» пандемию COVID-19, и я мог бы свести многие, если не все эти ошибочные шаги к двум проблемам: первая – это непонимание, что такое наука, и нежелание прислушиваться к ученым; а вторая – отсутствие сопереживания простым людям, чья жизнь резко перевернулась или даже оборвалась из-за этого вируса или его последствий. Отсутствие эмпатии – одна из основных причин нашей неспособности эффективно решать мировые проблемы. В удивительной книге Лесли Джеймисон «Экзамены по эмпатии» рассматриваются многие аспекты этой темы^[120]. То есть наша цель состоит в том, чтобы уменьшить боль и страдания от скорби, но не устранить ее полностью.

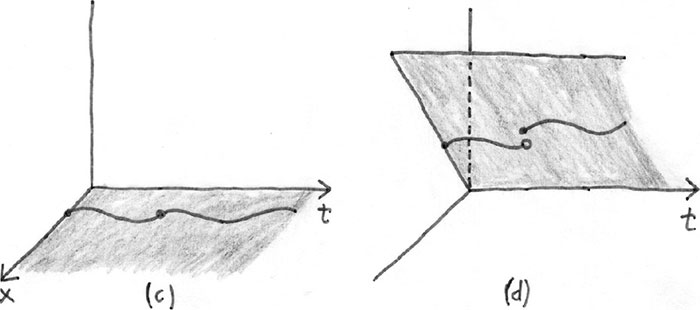
Нам потребуется наглядно показать это в пространстве повествования. Для начала рассмотрим проекции как тени. При ярком свете солнца или лампы вытяните руку вперед и растопырьте пальцы так, чтобы отбрасываемые ими на дорожке или на полу тени как можно дальше отстояли друг от друга. Затем поворачивайте руку, наблюдая за тем, как сближаются тени ваших пальцев. Попробуйте уменьшить расстояние между тенями, но не настолько, чтобы они наложились друг на друга. (Еще более удивительный пример такой игры вы найдете, если погуглите книгу «Гёдель, Эшер, Бах»^[121]. На обложке изображена тень от двух деревянных резных фигурок, висящих одна над другой и освещенных с трех сторон. На одной вертикальной плоскости фигурки отбрасывают тени в виде G над E, на перпендикулярной ей вертикальной плоскости – в виде E над G, а на горизонтальной плоскости – в виде буквы B).

Перейдем к нашей модели, представленной в серии из четырех рисунков (см. на предыдущей странице). На первом рисунке (а) мы видим траекторию, проходящую через трехмерное пространство, где оси x и y обозначают величины, значимые для пространства повествования, а t обозначает время. Отметим, что в точке разрыва происходит скачок траектории относительно оси y, тогда как значение по оси x остается постоянным.

На рисунке (b) мы видим проекцию (или тень) траектории на затененной плоскости y-t, то есть на плоскости со значением x = 0. Так как скачок, изображенный на рисунке (а), происходил лишь в направлении оси y, проекция на рисунке (b) демонстрирует скачок такой же величины, что и на рисунке (а).

На рисунке (с) изображена проекция траектории на плоскости x-t, то есть плоскости со значением y = 0. Поскольку при скачке величина x оставалась постоянной, эта проекция не показывает никакого скачка. Поэтому мы называем ее нулевой проекцией. Скачкообразное изменение произошло лишь для значения y, а в данной проекции эта переменная отсутствует. Такая проекция вряд ли нужна.

На рисунке (d) изображена проекция траектории на плоскости, где y = x. Здесь видно, что величина разрыва уменьшилась. На самом деле, регулируя наклон плоскости (то есть значение m на плоскости, выраженное как y = mx), мы можем получить разрывы разной величины. Чтобы изменение наклона m имело смысл, у нас должна быть возможность назначать масштабы осей, чтобы их можно было сравнивать. Если величину скачка соотнести со степенью душевного страдания, такая проекция способна навести нас на мысль о том, как сосредоточить наше внимание на нескольких факторах, чтобы уменьшить свою боль от необратимой утраты.

Попытаюсь привести пример. Чтобы успокоить душевную боль после смерти нашего кота Скраффи, некоторое время я пытался действовать так же, как при физической боли. Вместо того чтобы игнорировать неприятные чувства, я сосредотачивался на них, отметая всё остальное, пока не оставалась лишь боль. Иногда, хотя не всегда, боль становилась неузнаваемой, чужой, она переставала быть моей проблемой. Я не знаю, как это происходит, почему мои чувства отделяются от самого ощущения боли. Можно ли данный подход применить в отношении скорби?

(Этот метод уменьшения боли, который, признаться, имел всегда лишь ограниченный – хотя и ненулевой – успех, был навеян одним случаем из детства. Мы с братом Стивом спали в одной комнате, которую отец устроил, расширив чердак нашего дома. Однажды летом посреди ночи окна резко распахнулись от ветра. Залаяла собака. Стив спросил, что это за звук. Думаю, он хотел спросить, чья собака залаяла. Но я воспринял вопрос буквально и ответил: «Это просто собака». Стив повторил: «Собака». Я отозвался: «Собааака». И так мы перекидывались этим словом десятки раз. Наконец, мы оба заметили, какое это странное слово – «собака». Мы перестали видеть связь между звуками, составляющими слово «собака», и одомашненным дальним родственником волков. Благодаря многократному повторению и фокусированию внимания на звуке семантическое значение слова стерлось. Я полагаю, так бывает всегда, когда необычно странная последовательность звуков, обозначающих знакомый класс предметов, вдруг заслоняет собой привычное понятие.)

Хотя сосредоточенность на чем-либо и отбрасывание всего остального позволяет играть словами и звуками, это не помогло мне справиться с болью от потери Скраффи. Нужен был другой подход. Может быть, если отвлечься, это поможет, хотя сама идея мне не нравилась. Казалось, что, отвлекаясь от скорбных мыслей, мы отрицаем или, по крайней мере, приуменьшаем значимость Скраффи для нас. Я стал вспоминать о мелких эпизодах из жизни Скраффи: как он запрыгивал с пола к нам на плечи; как садился у открытого окна и, глядя через защитную сетку, мяукал, издавая звуки, похожие на щебет птиц; как забирался на полку в полуподвале и мочился на стопку старых научных журналов; а когда я растягивался на диване, ломая голову над очередной геометрической задачей, он устраивался у меня на груди, засунув голову под мой подбородок. У меня в голове проносились десятки подобных воспоминаний. Сами по себе эти воспоминания (даже то, как он мочился на журналы) лишь усугубляли ощущение необратимой утраты. Такой способ не работал. Но тут я стал думать о других котах, в основном соседских – о Билле и Уэйде. О том, что они, бывало, выделывали у меня на глазах. Рози привлекал запах печенья, и она терпеливо сидела на кухне в ожидании кусочка свежеприготовленного теплого лакомства. Принцесса и ее братик Вильгельм любили гоняться за шариком из алюминиевой фольги, они хватали его и приносили к нашим ногам, чтобы мы бросили его снова. И хотя все коты разные, эти штрихи перекидывали мостик над бездной, открывшейся с исчезновением Скраффи. Его больше нет; я могу видеть его лишь в своих воспоминаниях, которые, я знаю, со временем будут стираться. В этом смысле я буду терять его снова и снова. Но многое, что я любил в нем, я могу любить – и люблю – в других котах. Благодаря годам, проведенным со Скраффи, я стал гораздо лучше и несколько по-другому понимать кошек, а возможно, и людей тоже. Эти узы не устранили скорбь, которая камнем легла на мое сердце после его смерти, но они показали мне, насколько годы, проведенные со Скраффи, изменили мой образ мыслей. Одна дверь закрывается, другая открывается.

Теперь я думаю, что, благодаря счастливой случайности или моему чутью (скорее, всё же случайности), я спроецировал боль от потери Скраффи в пространство его повседневных проделок и проделок других котов. Хотя я не знал на тот момент, почему так вышло, но это помогло. Теперь у меня есть теория.

Прежде чем применить идею проекции, необходимо проработать как минимум три аспекта.

• Неединственность. Уменьшить боль утраты, вероятно, можно с помощью проекций на множество разных подпространств, сочетая множество разных эмоций. Представьте тень от карандаша, который держат перпендикулярно поверхности стола. Если источник света находится практически на оси карандаша, тень будет короткой. Если понемногу двигать источник света вокруг карандаша, он будет отбрасывать короткие тени в разных направлениях. Из множества доступных для проекции подпространств выбирайте самое привычное для вас.

• Движущаяся мишень. Подумайте о том, насколько ваша внутренняя модель внешнего мира изменилась за последний год. Подумайте, как она изменилась даже за сегодняшний день. Что стало важным для вас теперь и не было важным раньше? Что казалось раньше весомым, а теперь кажется ерундой? Насколько мне известно, заранее спланировать проекции невозможно. Их надо создавать в реальном времени.

• Калибровка. После того как вы выбрали подпространство, на которое будете проецировать свою скорбь, чтобы в заданной степени уменьшить боль утраты, как узнать, сколько следует уделить внимания категориям, определяющим это подпространство? В конце данной главы я приведу пример возможного подхода к этому вопросу. В пространстве повествования имеет значение наклон плоскости (или ее более многомерного аналога), на которую осуществляется проекция.

Не знаю, может ли мой подход помочь людям, не обладающим преимущественно геометрическим или визуальным мышлением. Однако мысленное проецирование на другие плоскости помогло мне создать свой способ для уменьшения боли утраты. Первые два аспекта вам следует проработать самостоятельно. Я призываю вас зримо представить, как различные факторы связаны между собой. Мысленно повращайте эти фигуры. Поначалу будет трудно, но я убежден, что в плане ясности и свободы геометрическое мышление не имеет себе равных.

Бенуа Мандельброт, с которым я проработал двадцать лет и который содействовал моему переходу из Юнион-колледжа в Йельский университет, обладал удивительной способностью к геометрическому мышлению. Он рассказывал, как во Франции на вступительном экзамене в университет ему попалась особенно трудная задача на тройной интеграл. Когда оценки были выставлены и Бенуа получил возможность поступить в любой французский вуз по своему выбору, школьный учитель математики сказал ему, что во всей стране только один ученик решил эту трудную задачу, и этот ученик был из его класса. Он (учитель) не смог вычислить этот тройной интеграл за отведенное время. Удалось ли это Бенуа? Да. Но как? Бенуа сказал: «Я покрутил в уме эту фигуру и заметил, что при определенном изменении координат тройной интеграл сводился к объему сферы, а объем сферы я знал».

Надписи на рисунке:

Игры Скраффи; игры других котов.

Когда Бенуа впервые рассказал мне эту историю, я еще больше почувствовал свое ничтожество, хотя Бенуа и его жена Алиетт всегда были неизменно добры ко мне и к моей Джин. Но в итоге я признал – для того, чтобы заниматься геометрией, мне необязательно владеть ею на том же уровне, что и Бенуа. У каждого из нас разные способности. Развивайте свои.

В следующей главе мы рассмотрим подход к моему третьему аспекту, калибровке, основанной на выборе масштаба. А пока я дам вам простой пример обычного выбора шкалы. На рисунке с предыдущей страницы вертикальная ось, обозначенная как «игры Скраффи», отражает удовольствие, которое я испытываю, глядя на хитроумные проделки Скраффи. Ось, обозначенная как «игры других котов», отражает удовольствие, которое я испытываю, глядя на изобретательные игры других котов. В подпространстве плоскости «игры Скраффи»-время t в моей траектории образовался большой разрыв, когда Скраффи умер. После его смерти ощущение радости не упало до нуля, поскольку воспоминания всё же доставляют некоторое удовольствие.

В подпространстве «игры других котов»-время t мое чувство радости остается неизменным, не столь сильным, как удовольствие от наблюдения за играми Скраффи, но несомненно более сильным, чем от моих воспоминаний о проделках Скраффи. Заштрихованная плоскость – это подпространство, где я иногда думаю об играх других котов, а иногда вспоминаю об играх Скраффи. Следовательно, падение настроения после смерти Скраффи здесь не такое значительное, как было в подпространстве «игры Скраффи»-время^[122].

Точная калибровка может оказаться трудной задачей. Нужно придумать, как сравнить величину моей радости от наблюдения за Скраффи и другими котами. В любом случае практическое применение требует каким-то образом определить эти шкалы. Можно просто подменить шкалу подсчетом относительного количества раз, когда я вспоминал игры Скраффи, и количества раз, когда я наблюдал за играми других котов. Следует подчеркнуть, что наблюдение за другими котами не отвлекает меня от воспоминаний о Скраффи, а, наоборот, напоминает о нем, поскольку некоторые его повадки свойственны и другим котам. Но я не хочу забывать Скраффи, поэтому стараюсь, чтобы время, когда я вспоминаю о Скраффи, не было слишком мало по сравнению со временем, когда я наблюдаю за игрой других котов. При таком мысленном подходе калибровка происходит сама собой.

Чтобы применить эти идеи к более сложным отношениям, к людям, которых мы потеряли, потребуется гораздо более сложный подход. Здесь приведен лишь простой пример того, как работает калибровка.

Я использовал геометрию, потому что хорошо ее знаю, за шесть десятков лет она прочно впечаталась в мое сознание. Поэтому игра различными геометрическими формами легла в основу подхода, который поможет вам найти свои комбинации ощущений. Вы можете достичь той же цели и иными путями. Возможно, ваше восприятие мира более слуховое или тактильное. Или вашу жизнь постоянно сопровождают отрывки мелодий. Тогда музыка может помочь вам найти то, что соответствует моим проекциям.

Или литература, или кино, или шахматы, или кулинария, или танцы, или бесконечное времяпрепровождение в компании котиков. Всё, что важно для вас, может навести на ту проекцию, которая уменьшит вашу скорбь. Однако это сработает, только если у вас есть настоящая страсть к своему делу. Вы можете найти способы, которые я даже не могу представить, чтобы открыть для себя комбинации ощущений, позволяющие уменьшить остроту скорби.

5. Фрактал

Один день – это лаборатория жизни.

Мы уже рассмотрели самоподобие некоторых фигур, в частности треугольника Серпинского. Правильный равнобедренный треугольник, изображенный вверху следующей страницы, состоит из трех частей – нижней левой, нижней правой и верхней левой, – каждая из которых является копией целого треугольника, уменьшенной в масштабе 1/2. Таким образом запускается процесс, который можно продолжать до бесконечности: каждая из трех частей будет состоять из трех меньших частей, из которых каждая, в свою очередь, будет состоять из трех еще меньших частей и так далее. Фигуры, обладающие таким типом симметрии – симметрии кратного увеличения, – были известны художникам и создавались ими на протяжении по меньшей мере тысячи лет.

Более естественные фракталы можно получить с помощью процесса декалькомании (см. изображение внизу слева на следующей странице). Краска сплющивается между двумя поверхностями; когда поверхности разворачиваются, меж них проникает воздух и создает замысловатые разветвляющиеся узоры. Эта техника известна уже как минимум несколько столетий, но наибольшее распространение получила лишь в начале XX века, в частности в работах Макса Эрнста, Оскара Домингеса, Бориса Марго и Ханса Беллмера. Сложные разветвления придавали их картинам сюрреалистический, сновиденческий характер.

Природа изобилует естественными фракталами. Облака, горные хребты, береговые линии, речные системы – все они лишены натурального масштаба. Не имея иных ориентиров, невозможно сказать, видите ли вы перед собой, например, маленькое облако вблизи или большое вдали. Подобные структуры встречаются на многих уровнях. На нижнем фото слева мы не видим масштаба, а на втором фото зажимы выдают размеры устройства: мы вырастили фрактальный дендрит, пропустив слабый электрический ток через раствор сульфата цинка.

Фракталы встречаются и в литературе. Например, Жозе Сарамаго так определяет геометрию кладбища, описанного в его романе «Книга имен»:

Был в моей жизни момент, когда я, сам того не замечая, оказался глубоко погружен в такую таинственную область, как фрактальная геометрия, о которой, уж простите мое невежество, до той поры совсем ничего не знал^[123].

Сарамаго описывает расположение надгробий в виде разветвленного дерева: самые старые могилы ближе к стволу, наиболее новые – на концах ветвей. В 1999 году испанский математик Хуан Мануэль Гарсия-Руис обратил внимание Сарамаго на фрактальную геометрию этого кладбища. И действительно, фрактальная геометрия – это огромная научная область^[124].

Мы приводим данные примеры, чтобы показать широкую палитру фрактальности, и чтобы вы, глядя на (неизбежно неправильные по форме) природные фракталы, не говорили: «Постойте, но это совсем не похоже на треугольник Серпинского». Мы ищем мотивы, которые приблизительно повторяются при изменении масштаба в пространстве, во времени или в каких-то более абстрактных координатах.

Вот вам примеры подобных структур в масштабах времени:

Возьмем день. Вы просыпаетесь засветло, думаете о предстоящих делах. Утром вы уже вовсю трудитесь; вечером вы заканчиваете работу и мысленно подводите итог сделанному за день. День закончен, вы ложитесь спать.

Возьмем год. Во тьме зимы вы думаете о том, что будете делать в этом году. Весной вы уже вовсю работаете над своим годовым проектом; осенью бо́льшая часть работы выполнена, и вы подводите итог сделанному за год. Наступает зима, год закончен, вы отдыхаете.

Возьмем жизнь. В детстве и юности мы осваиваем навыки для работы в будущем. В молодости вы вовсю включаетесь в работу; в старости выходите на пенсию и подводите итог сделанному за свою жизнь. Жизнь заканчивается, вы погружаетесь в сон небытия.

Конечно, этот грубый набросок не отражает всего богатства и разнообразия жизни, но он позволяет увидеть мотивы, повторяющиеся в различных временны́х масштабах. Почему мы обращаем на это внимание помимо того, что мы просто от природы склонны искать повсюду мотивы? Потому что день становится лабораторией года и целой жизни. Чтобы повлиять на траектории в более долгих временны́х масштабах, попробуйте, в качестве эксперимента, что-то изменить в масштабе одного дня. Как вам такая аналогия? Эксперименты в краткосрочном масштабе прекрасны тем, что можно попробовать много разных изменений и увидеть их краткосрочные последствия. Фрактальность предлагает условия для проверки гипотез в малом масштабе с последующим переносом в более крупный масштаб.

Я постараюсь доказать, что скорбь бывает разных масштабов, как по длительности во времени, так и по силе страдания. Если мы поймем, как справиться со скорбью в малых масштабах, может быть, это поможет справиться и со скорбью больших масштабов?

На самом деле, мы уже говорили об опытной лаборатории по работе со скорбью: в третьей главе такой лабораторией стала геометрия (вы можете заменить геометрию на область, наиболее интересную вам). Это был новый для вас раздел. В третьей главе я использовал фрактальную геометрию, потому что немногие детально знакомы с этим предметом. Это наиболее зрелищная часть геометрии, которая может преподнести сюрпризы практически каждому. (На самом деле, просто каждому. Когда кто-то показывал Бенуа Мандельброту новые вычисления, эксперимент или наблюдение, связанные с фракталами, на его лице был написан восторг. Этот обычно сдержанный человек, гений на пике своей карьеры, превращался в маленького ребенка, увидевшего в ночном небе метеор – яркую световую черточку там, где мгновение назад была тьма.) Мы продолжим разговор о фрактальной геометрии и сделаем вывод, который у многих вызывает удивление: размерность не всегда выражается целым числом.

Возьмем, к примеру, отрезок прямой, треугольник Серпинского и заштрихованный квадрат (см. ниже). Если в два раза увеличить высоту и ширину каждой фигуры, мы получим, соответственно, две, три и четыре копии изначальной фигуры. Отрезок – одномерная фигура, а квадрат – двумерная, и когда мы увеличиваем высоту и ширину этих фигур, получаем, соответственно, 2 = 2¹ копии линейного отрезка и 4 = 2² копии заштрихованного квадрата. Для этих, как и для всех самоподобных фигур, размерность является экспонентой. Поэтому размерность d треугольника Серпинского определяется как 3 = 2^d. Итак, 2 = 2¹, а 4 = 2², значит, размерность треугольника больше единицы, но меньше двойки. По мере увеличения треугольник растет быстрее, чем одномерный отрезок, но медленнее, чем двумерный заштрихованный квадрат^[125].

Треугольник Серпинского находится где-то между одномерностью и двумерностью. Пытаясь понять это явление, некоторые из моих студентов вначале думали, что между одномерностью и двумерностью может быть узкая полоска на плоскости. Полоска не занимает всю плоскость, поэтому, рассуждали ученики, она меньше, чем двумерная. Но она толще линии, а значит, более чем одномерная. Второе утверждение близко к истине благодаря так называемой монотонности размерности: размерность одной части не может быть выше размерности целого. А вот первое утверждение более проблематично, поскольку любая фигура, имеющая площадь, является двумерной. Узкая полоска на плоскости двумерна. Но треугольник Серпинского обладает бесконечным количеством отверстий, и площадь этих отверстий добавляется к площади большого треугольника, поэтому площадь треугольника Серпинского равна нулю^[126].

Фрактальная размерность применяется во многих областях, в первую очередь при многократном измерении неровностей природных объектов. Расширение понятия размерности на области психологии или чувственного восприятия – задача непростая, однако вот вам финальный довод, или, скорее, догадка, или даже пожелание. Самоподобие скорби подразумевает, что на малых жизненных утратах мы можем испытать способы адаптации к большим утратам. Можно ли определить размерность проекции и, основываясь на этом, измерить, пусть и приблизительно, насколько прочно связаны между собой большие и малые утраты? Пока что я этого не знаю. Но, возможно, когда-нибудь узнаю.

Предварительно ответим на такой вопрос: «Если бы вы жили в мире, где размерность пространства выражается нецелым числом, как бы выглядело всё вокруг?»^[127] А что, если размерность времени не выражается целым числом?

Вопросов больше, чем ответов, да и то это не совсем вопросы, скорее – фантазии.

Когда вы впервые сталкиваетесь с идеей фрактальной размерности и осознаёте, к чему она может привести, ваш взгляд на мир переворачивается. Едва мои студенты улавливали ее суть, я видел, как по аудитории проходили волны изумления (так реагировало большинство) или головокружения (так реагировали немногие).

Вот почему преподавание было для меня таким удивительным занятием и почему я оставил его, только оказавшись в больнице. Даже сейчас, по прошествии пяти лет после ухода из преподавания, я по-прежнему мечтаю о нем. Проснувшись утром, я думаю о том, что совершил ужасную, страшную ошибку, когда ушел на пенсию.

Сложность визуальных образов, шероховатость древесной коры, пушистость облаков, густота ветвей или листьев папоротника – всё это теперь представляется вам в виде числа. Осознав это впервые, вы говорите себе: «В жизни бы не подумал, что существует вот такое понимание сложности мира». А теперь вы узнали новый способ измерить эту сложность. Но со временем чувство удивления тускнеет, первый шок открытия уже не повторится, а от того благоговейного трепета, когда вы впервые посмотрели на мир новыми глазами, остается лишь горечь необратимой утраты.

Можно ли восстановить отзвук того первого ощущения? Вероятно. Можно спроецировать наше удивление от открытия нецелочисленных размерностей на множество разных ситуаций. Распространить простую формулу, в которой все части фрактала одинаковы по размеру, на самоподобные фигуры с различными масштабирующими множителями, на фракталы, для которых разрешены лишь некоторые сочетания преобразований (мы видели такой пример в первой главе, на с. 46, 47), на фракталы, где масштабирующий множитель выбирается случайным образом, на фракталы, где масштабирование является нелинейным, и так далее. Простую формулу фрактальной размерности (приведенную в Приложении) можно распространять на всё большее количество областей, и эти версии будут нести на себе отпечаток изначальной формулы. Каждое из таких расширений становится маленьким сюрпризом и дает толчок, напоминающий тот первый шок, который вы испытали, узнав о нецелочисленных размерностях.

По мере того как у нас накапливаются эти похожие формулы, мы видим, что все они – тени одной большой картины. Проецируя в различные пространства скорбь утраты нашего первого сильного впечатления от встречи с нецелочисленными размерностями, мы сможем немного облегчить эту боль, испытывая нечто отдаленно похожее на то, первое удивление. Посмотрите, что произошло в нашем примере: совокупность проекций показала, что существует некий более глубокий общий мотив. Можно ли такой обратный ход перенести на другие случаи скорби – от потери близкого человека или домашнего животного?

Насколько мне известно, все формы скорби одинаковы: для них характерна необратимая утрата чего-то или кого-то необычайно дорогого вашему сердцу и в то же время некий налет трансцендентности. Эти чувства, разумеется, могут быть весьма неодинаковы по своей силе. Горечь от того, что нельзя заново пережить тот момент перестройки сознания, который сопровождал ваше знакомство с нецелочисленной размерностью, менее глубока, чем скорбь от потери домашнего животного, а она, в свою очередь, менее глубока, чем скорбь от утраты близкого человека. Скорбь может различаться по степени интенсивности, но по своей сути – нет. По крайней мере, мне так кажется.

И здесь мы приходим к еще одному моменту: любая скорбь состоит из множества своих подвидов, более мелких скорбей. Теряя близкого человека, мы также теряем возможность снова увидеть его реакции, его действия. Каждое действие складывается из более мелких действий, из многих мелочей, и мы теряем возможность снова увидеть каждую из них. И так далее. Если все мелкие скорби одинаковы, значит, скорбь самоподобна. Признав это самоподобие, мы определим те проекции, которые помогут нам умерить скорбь. Всё это слишком абстрактно. Давайте проиллюстрируем основную идею на более интуитивном примере, нежели вычисления размерностей для череды всё более неправильных форм фракталов.

Вернусь к универсальному примеру скорби – утрате родного человека. На сей раз расскажу о смерти отца. Мама умерла неожиданно: ударил инсульт – и ее не стало. После маминой смерти папа прожил еще семь лет. У него были проблемы со здоровьем: диабет, коронарное шунтирование, эмфизема и асбестоз. Последние две болезни он заработал на верфях Ньюпорт-Ньюс в начале Второй мировой войны: поначалу в его обязанности входило распыление асбеста между стенами складов с корабельными боеприпасами. В конце он уже стал помощником электрика, и многие из посадочных огней на авианосце «Йорктаун» были установлены его руками. Однако работа с асбестовой изоляцией, которая в конце смены превращала его в снежного человека, причем без респиратора, – она его всё же доконала. Ну и полувековой стаж курения тоже.

Пять лет после маминой смерти отец прожил в том же доме, бо́льшую часть которого он построил и переделал сам. Он немного научился готовить, стирать и прибирать. Зависимость от кислородного баллона не давала ему далеко уезжать. Отец попросил мою сестру подобрать для него какое-нибудь занятие, и она записала его в секцию оздоровительной гимнастики. Он стал передвигаться на машине только по городу. Сент-Олбанс – городок небольшой, поэтому далеко он не ездил. Но здоровье его становилось всё хуже. Отец начал путаться, не всегда узнавал знакомых людей, включая меня. Потом он стал бояться жить один и на ночь клал под подушку пистолет. Однажды ночью отец проснулся от какого-то шума, доносящегося с задней террасы. Встав с кровати, он взял из-под подушки пистолет и, пройдя через весь дом, подошел к задней двери. Он включил свет на террасе, открыл первую, деревянную, дверь и сквозь вторую, стеклянную, увидел голого человека с пистолетом. Отец поднял пистолет, человек на террасе тоже поднял пистолет. И тут отец понял, что едва не выстрелил в собственное отражение. (О том, что мой отец спит голым, я узнал, только когда он рассказал мне эту историю.) Вскоре после этого он попросил перевезти его в дом престарелых. Моя сестра нашла для него хороший приют. Папа продал дом и переехал в то место, которое выбрала ему Линда.

Там он прожил полтора года. Приезжая к нему, другие члены семьи выполняли его мелкие поручения или привозили старых друзей. Поскольку я так и не научился водить машину, то просто сидел рядом с папой: он – в своем кресле-качалке, я – на диване. Обычно он ставил какой-нибудь ковбойский фильм на DVD, хотя иногда я подсовывал ему кино с Джимми Стюартом или старый фильм Альфреда Хичкока. Мы немного болтали. Вскоре отец засыпал. Насколько я мог судить, он всё время пересматривал одни и те же фильмы. Если кто-то его спрашивал почему, он отвечал, что каждый раз видит в них что-то новое. Возможно, он каждый раз просыпался на разных эпизодах. Я просил отца рассказать о его детстве в Роздейле (Западная Виргиния) в период Великой депрессии, или о том, как он служил на Тихоокеанском флоте во время Второй мировой, или о первых послевоенных годах, когда он еще ухаживал за мамой. У него было две дюжины любимых историй, и, когда я приезжал, он обычно рассказывал что-нибудь из своих хитов. Иногда я слышал что-то новенькое, но как правило – нет.

В начале 2016 года отцу резко стало хуже. Несколько недель он провел в больнице, затем в хосписе, а потом умер. В последние дни перед уходом он жил в какой-то иной реальности, нежели все окружающие. Он сказал Линде, что однажды ночью разговаривал со своей женой (семь лет как покойной), рассказывал ей, как хорошо о нем заботятся дети. По его словам, мама ответила: «Ну, а как же иначе?» Так он прожил еще несколько дней, и однажды утром его не стало.

Поскольку отец был ветераном флота, ему полагались военные почести. Я и раньше бывал на военных похоронах, поэтому знал процедуру. Поскольку после маминой смерти Линда так много сделала для папы, так заботилась о нем, особенно в его последние годы жизни, мы со Стивом попросили женщину – флотского капеллана передать флаг Линде. Я держался, пока капеллан читала «Молитву о моряке» и когда моряки необычайно аккуратно и торжественно складывали флаг, покрывавший гроб отца. Я держался, когда один из моряков, преклонив колено, подал флаг Линде. Она этого не ожидала и расплакалась. Я думал, что за последние дни выплакал все свои слезы, но, когда капеллан произнесла: «Закройте уши, сейчас будет громко», – я понял, что ошибался. Семеро отставных моряков и солдат сделали по три выстрела, затем горнист сыграл «Отбой» – самую печальную музыку на свете. У меня перехватило дыхание, потоки горячих слез полились из обоих глаз, а мой плач походил скорее на писк.

Оправившись немного, я поблагодарил капеллана. Она сказала, что иногда ей бывает трудно найти семь человек для ружейного салюта, но, поскольку отец был ветераном Второй мировой войны, желающих было полно. «Если вы никогда не служили, вам не понять, какая это честь – выказать уважение человеку, реально участвовавшему во Второй мировой. Ваш отец был героем». Для меня, для Линды, для Стива отец всегда был героем, но я никогда не думал, что он может быть героем для кого-то еще. И отчего-то у меня снова полились слезы. Да что же это такое? Неужели, когда я не плачу, у меня внутри столько воды?

Возвращаясь в Коннектикут, мы с Джин много вспоминали о времени, проведенном с отцом. О том, как много в нашем доме было сделано его руками; о том, как вскоре после нашей свадьбы мои родители прокатили нас по всей Западной Виргинии, чтобы Джин, которая выросла на Верхнем полуострове Мичигана, «познакомилась» с нашим штатом; о том, как вечерами, уже после смерти мамы, отец сидел на задней террасе и смотрел, как зажигаются в небе звезды, а под ними летают светлячки; о том, как в один из таких вечеров мы заговорили о мечтах, о сожалениях, о призрачности прошлого и будущего. От этих воспоминаний становится легче. И вот мы уже снова вместе с папой чиним электрический щиток у нас в доме; или проезжаем вместе с ним, мамой и Джин мимо радиотелескопа Грин-Бэнк; или наслаждаемся первой прохладой летнего вечера и удивляемся, как это мой старый отец вдруг смог понять и обсудить с нами идеи на три порядка более глубокие, чем те, что мы обычно с ним обсуждали. Может, я недостаточно понимал его в эти последние шестьдесят пять лет?

Воспоминания дарили облегчение на пару минут, но слишком быстро улетучивались. И всё же вскоре после душераздирающих папиных похорон боль утраты немного отступила. Почему? Разумеется, я любил папу не меньше, чем маму, а мамина смерть жгла меня долгие годы. Думаю, разница в том, что я успел привыкнуть к папиному уходу. Он не исчез так внезапно, как мама. В последние годы своей жизни папа уходил постепенно.

Сначала трудности с дыханием вынудили его оставить работу в мастерской. В какой-то момент он понял, что больше туда не войдет. Я тоже это понимал и страдал от необратимости такой ситуации. В этой мастерской мы с папой создали сотни разных вещей. Пока я не поступил в колледж, у меня была лаборатория в углу той мастерской. Когда я понял, что больше он не будет ничего мастерить, я вспомнил, чем мы с ним занимались: чинили соседскую газонокосилку, строгали рамки для картин и ящички, делали деревянные пазлы и машинки для соседских детишек. Я сосредоточился на поступках, а не на чувствах, представлял, как другие люди так же помогают соседям. Я увидел сделанное руками отца (иногда при моем участии) частью более широкой картины. И хотя отец уже никогда ничего не смастерит, движение «сосед помогает соседу», сама эта идея, которая была близка моему отцу, продолжает жить. Проекция в пространство «добрососедской помощи» облегчила мою скорбь, когда отец закрыл свою мастерскую.

Похожая, но более сильная боль поразила меня, когда отец продал дом. Мы с Линдой и Стивом там выросли. Он хранил столько чудесных воспоминаний. Вечерами трое детишек, как щенки, собирались вокруг матери; мама читала книжки, папа чистил и разрезал яблоки, а потом раздавал их по кругу. Море смеха, порой споры, иногда слезы. Сколько было историй, совместных ужинов, разговоров. И дом рос вместе с нами. Папа добавил к нему одну комнату, затем другую. Мама шила занавески и копалась в саду. Сама форма комнат, геометрия пространств была оболочкой нашей жизни. Потом мама умерла. А папа переехал в пансионат и продал дом. И это тоже было необратимо. Мы больше никогда не будем в нем жить. И эта утрата стала источником скорби. Пара, купившая дом, ждала своего первого ребенка. Они предложили цену сразу, как только впервые пришли на просмотр. Улучшения, сделанные моим отцом, были продуманными и надежными; отец был рад, ему польстило, что он так быстро получил хорошее предложение. Когда я разговаривал с папой сразу после продажи, он сказал, что дому нужна семья и что он счастлив от того, что в нем будет снова расти ребенок. Он был прав. Дабы умерить скорбь от потери нашего дома, надо спроецировать маленькие детали нашей жизни на жизнь другой семьи.

После папиной смерти, когда закончились душераздирающие похороны и отгремел двадцать первый выстрел салюта, исторгший из моих глаз невообразимые потоки горячих слез, я вспомнил о том, как мы справились со своей скорбью после потери мастерской, а потом и дома. Мы спроецировали ту скорбь в пространство мелких деталей и взаимодействий с другими людьми. Всё, что отец делал для других людей – помогал соседям с ремонтом, помогал в строительстве дома своим родным и друзьям, всегда был рад выслушать других и поделиться своими рассказами, – оставило отпечаток не только на тех людях, которым он помогал. Его дела, а также то, что мама готовила и шила для других, являли образец доброты и душевной щедрости. И всё это понемножку оказывало свое влияние на мир. Это и есть истинное наследие моих родителей. Их больше нет. Я никогда их больше не увижу, никогда не поговорю с ними. Но их неспешный, терпеливый и надежный труд помог людям найти верный путь. «Двигайся маленькими шажками», – говорил мне отец, когда я упирался в какую-либо проблему. Совершая маленькие шажки, они сделали мир прекраснее, чем он был до них. В самом деле, это лучшее, на что способен практически любой из нас.

Такие проекции, вероятно, помогут не каждому. Я пока не нашел универсальной проекции для всех. Может быть, ее не существует, а может быть, я недостаточно гениален для этого. В моем нынешнем понимании, применение данного подхода зависит от человека. Самая тяжелая работа ложится на ваши плечи. Геометрическое выражение проекции – наглядный инструмент, который помог лично мне. Но если вы поняли мою идею и при этом далеки от геометрии, наглядность необязательна. Если вам удастся найти примеры скорби в уменьшенном масштабе, превратите их в лабораторию для поисков эффективных проекций. Затем, применив метод самоподобия, увеличьте масштаб. Если ваши малые примеры окажутся составными частями большой скорби, как это было в моем случае, то вы легко поймете, почему я говорю о самоподобии скорби. Надеюсь, вам удастся адаптировать мой подход к своим обстоятельствам.

Лара Санторо, журналистка и писательница, которая много лет рассказывала об эпидемии ВИЧ/СПИД в Африке, а значит, видела больше скорби, чем многие из нас, нашла способ избегать выгорания. Она называет это методом «широкого объектива». Вместо того чтобы полностью погружаться в момент, накрепко связывая себя с тем, что она видит, слышит и чувствует, Лара мысленно делает шаг назад и видит себя посреди всего этого безбрежного горя. Такой дополнительный уровень осознания накладывает особый фильтр на чувство сопереживания, которое иначе могло бы обостриться до предела. Да, ее по-прежнему окружает море отчаяния, и она могла бы сама погрузиться в него, но, глядя на себя как бы со стороны, она понимает, что это отчаяние не составляет всей картины. И этого достаточно. Боль осталась – ужасная боль, – но теперь ее можно вытерпеть. Лара позаимствовала эту идею у Спинозы, который говорил, что боль прекращается, или, по крайней мере, притупляется, как только мы ясно обрисовываем ее в своем воображении.

Метод проекции, который советую я, в основном связан с поиском уровней внутри скорби, ее подструктур. Взгляд Лары устремлен скорее вовне, нежели внутрь. Ее подход лишь внешне несколько похож на мой, требующий находить глубоко лежащий мотив в различных формах размерности. Я никогда не выхожу за рамки мира идей, тогда как Лара привносит в данный процесс что-то личное, сознание самой себя. Ее подход просто гениален.

Это вновь возвращает нас к сюжетам. Мне не хотелось бы заканчивать на пессимистической ноте, но, поскольку впереди еще одна глава, здесь я могу предостеречь вас, призвать к тому, чтобы вы поступили лучше, чем я, чтобы, оглянувшись назад на прожитую жизнь и найдя лишь горький пепел сожаления, вы навсегда не разбили свое сердце. Когда я начал писать эту книгу, то не был уверен, что вставлю эти слова. Теперь они кажутся мне абсолютно необходимыми. Если я передумаю, вы об этом никогда не узнаете.

И всё же сначала прочтите, что говорит Хелен Макдональд о том, как жизнь порой оборачивается иначе, чем ожидалось:

В жизни человека бывает такой период, когда кажется, что в вашу жизнь постоянно входит что-то новое. Но потом в один прекрасный день наступает прозрение, и вы понимаете, что так будет далеко не всегда. Вы замечаете, что жизнь превращается в существование, полное пустот. Лишений. Потерь. Совсем недавно нечто было вполне реальным – и вот его уже нет. А еще вы понимаете, что надо выстраивать свое бытие среди этих утрат, хотя можно протянуть руку туда, где находились ваши пропажи, и почувствовать напряженную, сияющую беззвучность пространства, заполненного воспоминаниями^[128].

На каждом этапе своей жизни я всегда делал удобный мне выбор. Мама хотела, чтобы я стал ученым-врачом, но я не пошел по этому пути, ведь он трудный и весьма беспокойный. Я знал, что у меня недостаточно способностей для великих открытий, но я всё же мог принести какую-то пользу. Вместо медицины я занялся физикой и математикой, постарался убедить себя, что абстрактная наука в некотором смысле «лучше», чем прикладная. Чепуха: это лишь способ спрятаться от ответственности. Если бы я занялся биомедициной, мои ошибки могли бы навредить людям, причем даже серьезно. Но если бы, изучая высшую математику, в третьем семестре я ошибся в доказательстве теоремы Грина, никто бы не умер.

Я был достаточно умен, чтобы овладеть математикой, но не для того, чтобы заниматься сколько-нибудь значимыми исследованиями. Поэтому я решил преподавать. А так как я и сам вечно путаюсь, то всегда хорошо понимал недоумение студентов. Как правило, я его замечал и успевал исправиться прежде, чем они доходили до стадии под названием «пора задать вопрос». И я убедил себя, что преподаю, дабы помочь своим студентам. Возможно, так оно и было. По правде сказать, преподавание – благородная стезя. Моя сестра преподавала во втором-третьем классах сельской школы Огайо. Она – герой, а я ленивая скотина.

Вся моя энергия ушла на оттачивание преподавательских навыков. Когда мне было под шестьдесят, у меня появились первые когнитивные нарушения. Я больше не мог так же четко ориентироваться в идеях, порхающих в аудитории. Даже перед занятиями, которые я вел более десяти лет – и для которых мне раньше хватало пяти минут, чтобы заглянуть в свои записи и просмотреть, какие примеры, какие теоремы и какие практические задачи я представлю, – я стал ловить себя на том, что за час до лекции снова и снова просматриваю эти записи, надеясь хоть что-то удержать в голове. Иногда мне это удавалось, иногда – нет. Преподавание – единственное, что я хоть как-то умел делать, и теперь этот навык стал медленно исчезать у меня на глазах. Нейропсихологические тесты и томограмма вскрыли серьезные проблемы. Это была не просто возрастная усталость: я стал истончаться, чтобы однажды окончательно исчезнуть.

В этот печальный период жизнь подкинула мне несколько ироничных сюрпризов. Я упомяну лишь о двух, так как не стоит слишком утомлять вас рассказами о моих болячках. В 2014 году меня пригласили прочесть в рамках «Сектора нестандартного мышления» лекцию о фрактальной геометрии и сложном устройстве живых организмов на аспирантском симпозиуме в Венском биоцентре. Несколькими годами ранее, когда я еще был уверен, что смогу достойно выступить, я был бы счастлив поехать туда. Я никогда не посещал Вену, да и вообще Европу. Для меня это была бы отличная возможность. Но к 2014 году мой разум уже начал исчезать. С превеликой грустью я отказался и рекомендовал другого лектора, работавшего в тех же областях науки.

И, наконец, главная ирония судьбы: вернувшись домой после того, как я прочел последнюю в моей преподавательской карьере лекцию, я нашел в ящике своей электронной почты письмо от Математической ассоциации Америки с просьбой выступить в качестве приглашенного докладчика на «МатФест-2017» в Чикаго. Я обдумывал это всю ночь. Нам с Джин нравился Чикаго, и я довольно хорошо знал этот город, хотя к тому времени мы уже несколько лет там не бывали. Но в мае 2016 года я уже не мог быть уверен в том, что через год буду на что-то годен, поэтому опять с превеликой грустью отклонил предложение.

Скорблю ли я об утрате навыков, которые оттачивал десятилетиями? О том, что мне пришлось отказаться от приглашений, которые могли бы дать мне потрясающую возможность поделиться тем, чему я научился, работая с Бенуа Мандельбротом? Да и еще раз да.

В своем романе «Какой бы странной ни была эта погода» Энн Панкейк дает захватывающее описание скорби об утрате той жизни, которая могла сложиться иначе:

Я поняла, что значит оплакивать свою жизнь, которая еще не закончилась, и я поняла, что на свете мало бывает потерь горше этой. Эта скорбь абсолютно выходила за пределы моего воображения. Я до сих пор иногда ощущаю ее сухую шершавую вмятину. Хлесткий удар – и жгучая физическая боль^[129].

Самоподобие моего жизненного выбора – в малых, средних и больших вопросах я всегда выбирал безопасные, удобные для себя решения – породило самоподобие скорби: я сожалею о своем выборе в вопросах малого, среднего и большого масштабов. Пример малой скорби: зачем я выбрал второй цикл лекций по астрономии, а не пошел на генетику? Тут уже можно разглядеть зачатки скорби большего масштаба: ведь тогда я мог бы разрабатывать лекарства от болезней или лечить пациентов. Вместо этого я разрисовывал меловые доски диаграммами и уравнениями, пытаясь по кусочкам объяснить, как природа раскрывается в геометрии. Но тогда я даже не видел – и тем более не осознавал, – какие последствия будет иметь такое масштабирование.

Притупилась ли моя боль благодаря тому, что я сделал шаг назад и посмотрел на себя скорбящего со стороны? Да, немного. Такой взгляд, в общем, несколько облегчил мои страдания по поводу невыбранных дорог. Что бы я ни делал, моя карьера все равно рано или поздно завершилась бы, к тому же есть профессии, расставание с которыми приносит гораздо больше сожаления, нежели расставание с сорокалетней карьерой преподавателя.

Сделаете ли вы в своей жизни лучший выбор, чем я? Я этого не узнаю, но вы – непременно.

6. По ту сторону

Сияющая смелость доброты.

Джуда Перл

Как мы уже видели, понимание геометрии может помочь перенаправить наше восприятие, чтобы притупить невыносимую остроту скорби. Но закончим мы движением в ином направлении. Вместо того чтобы создавать проекции в различные подпространства наших ощущений, мы создадим проекцию в пространстве наших поступков. И также применим к ней масштабирование.

Прежде всего необходимо обратить внимание на индивидуальные различия. Когда мои родители умерли, сперва меня парализовала боль. Едва боль немного утихла, я стал то и дело получать удары наотмашь: когда, увидев что-то, что могло заинтересовать маму или папу, я уже начинал думать, как расскажу им об этом, и вдруг понимал: «Погоди, они же мертвы». Когда такие мысли перестали приходить ко мне на каждом шагу, я принялся заполнять огромные лакуны, оставшиеся в моем мире после ухода родителей. Но тут мама с папой стали являться ко мне во сне. Даже теперь они мне иногда снятся, обычно в каких-то обыденных ситуациях: то мы совершаем короткую поездку куда-нибудь, то я помогаю маме на кухне, то работаю с папой в мастерской. Просыпаясь, я заново осознаю, что их больше нет, и меня захлестывает краткая, но жгучая волна скорби, обычно сопровождаемая серией досадных ругательств.

Моей сестре Линде тоже снятся мама и папа, но она всегда просыпается радостной, ведь для нее такие сны – это способ повидаться с ними. Линда почти на два с половиной года моложе меня. У нас с ней много общего; мы оба стали преподавателями. Но мы совершенно по-разному реагируем на сны о наших покойных родителях. Вывод: нельзя ориентироваться на свои чувства, чтобы судить о чувствах других людей. Будьте беспристрастным наблюдателем.

Когда вы теряете близкого человека, окружающие из лучших побуждений могут сказать вам слова, которые вас расстроят или заденут. Большинство людей в такой ситуации способны произносить лишь банальности. Ненадолго спроецируйте себя в пространство поступков: даже если чьи-то слова вам не нравятся, будьте снисходительны. Им было бы больно услышать, что́ вы ощущаете на самом деле, поэтому постарайтесь сделать так, чтобы они почувствовали себя лучше. Конечно, скорбите именно вы, но обратите свое внимание вовне и помогите людям, пытающимся вас утешить. Если вам принесли еду, похвалите человека за заботу. Отчасти это вас отвлечет, но в целом вы почувствуете себя лучше, потому что помогать другим всегда приятно.

(Когда я говорю с человеком, только что потерявшим кого-то из близких, то всегда спрашиваю, могу ли я чем-нибудь помочь. Понаблюдайте и поймите, в чем человек нуждается. Я могу выполнить какое-то поручение? Позвонить куда-нибудь? Всегда лучше предложить что-то конкретное. А потом спросите, не хочет ли он рассказать что-нибудь о покойном. Возможно, всё это не поможет. На предложение помыть посуду он скажет: «Как ты можешь думать о посуде в такое время?» А просьба рассказать о покойном вызовет в ответ рыдания. Вспомните всё, что вы знаете о скорбящем человеке, чтобы понять, в чем он нуждается, а если не угадали, будьте готовы принять последствия своих действий.)

Скорбь дарит нам возможность спроецировать себя вовне, в поступки, которые могут помочь другим людям. Я привел в пример маленькие шажки, но даже они отчасти объясняют, почему групповой отбор способствует тем действиям, которые мы можем предпринять для переустройства своей жизни после утраты. Можно ли масштабировать эти скромные шажки? Существуют ли какие-то большие шаги?

На самом деле, иногда скорбь дарит нам возможность для совершения невероятно прекрасных поступков. Мои дедушки, бабушки, папа и мама умерли, и это были ужасные утраты. Но в сто раз хуже, когда родители теряют ребенка. У меня нет детей, поэтому я никогда не испытаю этого на себе. Скорее всего, я даже не могу представить себе чудовищную боль, когда ребенок погибает от болезни или в результате несчастного случая, а тем более в результате убийства или покушения. Сам вид такой скорби парализует, пусть даже я смотрю на нее лишь со стороны: я никогда не дарил любовь своим детям и не смогу узнать, каково их потерять. Но я могу представить, хотя и опосредованно, глубину подобного страдания.

Джуда Перл – гениальный ученый в области информатики; он разработал теорию каузального исчисления, описанную в его книгах «Каузальность» и «Почему? Новая наука о причинно-следственной связи»^[130]. Помимо прочего, каузальное исчисление объясняет загадочный клубок вычислений, называемый в статистике парадоксом Симпсона. Сын Джуды Перла, журналист Дэниел Перл, был похищен и убит в Афганистане в 2002 году. В ответ на это чудовищное, самое страшное событие, какое только может случиться с родителями, Джуда, его жена Рут, их родные и друзья создали Фонд Дэниела Перла, который способствует межкультурному взаимопониманию. Перед лицом столь невероятного зла это самый героический ответ, какой я могу себе представить.

В январе 2009 года ныне покойный кинокритик Роджер Эберт написал в своем дневнике, что он никогда не плачет во время грустных эпизодов в кино, зато плачет, когда показывается победа добра, в моменты душевного подъема, как он это называл, «возвышения»^[131]: «Меня трогает великодушие, сочувствие, храбрость и способность человека надеяться». В поступке Джуды и Рут вполне проявились все эти качества, и, когда я прочел об этом, у меня зачесались глаза, в горле появился комок и участилось дыхание. На следующий день, когда я кормил уличных котов, живущих в нашем дворе, меня сразила сила поступка семьи Перл. Я сел на ступени крыльца и зарыдал. Даже сейчас мне эмоционально трудно писать о сделанном ими выборе: столкнувшись с абсолютным ужасом, они решили прославить «сияющую смелость доброты» в жизни своего сына^[132].

Я не смогу описать путь, который привел семью Перл к такому поступку.

Лучше я дам свое толкование, опирающееся на разработанные нами здесь методики. Дэнни увлекался музыкой, значит, надо спроецировать утрату в пространство, включающее в себя его любовь к музыке. Музыка будет жить, стало быть, и влияние Дэнни, и его знания получат свой отклик. Эта утрата, которая всегда будет стоять перед глазами его родных, станет напоминать им подробности его жизни. У них больше не будет опыта общения с ним, но воспоминания о нем можно рассматривать с разных сторон и осознавать всё время по-новому. Если спроецировать память о Дэнни в пространство его поступков и интересов, эти воспоминания заиграют новыми красками. Но давайте посмотрим шире. К чему Дэнни стремился? Можем ли мы помочь людям, не знавшим его, почувствовать стремления Дэнни? Прекрасный и волнующий ответ, от которого перехватывает дыхание: да.

Смерть закрывает дверь к дальнейшему общению с теми, кого мы безвозвратно потеряли. Но скорбь открывает дверь – пусть даже крохотную щелочку – к тому, чтобы пересмотреть воспоминания и по-новому увидеть свои поступки. Давайте подумаем, какого поступка хотел бы от нас ушедший человек? За примерами далеко ходить не надо: «Вместо цветов семья просит сделать пожертвование туда-то». И это прекрасно, это замечательно. Дело, которым дорожил покойный, получает поддержку в память о нем. Он как будто всё еще с нами.

А некоторым людям скорбь распахивает двери храма и дарит возможность вернуться в мир и творить изумительное добро.

Появилась ли скорбь в процессе эволюции? Взглянем уровнем выше, с точки зрения эволюции общества: скорбь побуждает к поступкам, которые помогают многим людям.

Быть может, это лучший ответ на нашу боль: скорбь дает нам средство, чтобы сделать смелый шаг вперед.

Приложение: добавим математики

Заглянем под капот.

Здесь мы восполним некоторые детали, которые ранее не требовались, если в каких-то вопросах вы готовы были поверить мне на слово. Чтобы следить за моими рассуждениями, достаточно некоторого знакомства с математикой, по большей части с алгеброй из средней школы.

СКОЛЬКО КУБОВ ОГРАНИЧИВАЮТ ГИПЕРКУБ?

Единичный квадрат S на координатной плоскости xy состоит из всех точек (x, y), для которых 0 ≤ x ≤ 1 и 0 ≤ y ≤ 1. Чтобы найти все части границы квадрата S, зафиксируем одну из координат в своем крайнем значении 0 или 1, а вторая координата пусть изменяется в пределах интервала [0,1]. Таким образом, граница квадрата состоит из четырех ребер, каждое из которых является отрезком прямой.

(левое ребро) (правое ребро) (нижнее ребро) (верхнее ребро)

левое ребро x = 0, 0 ≤ y ≤ 1

правое ребро x = 1, 0 ≤ y ≤ 1

нижнее ребро y = 0, 0 ≤ x ≤ 1

верхнее ребро y = 1, 0 ≤ x ≤ 1

Единичный куб C в координатном пространстве xyz состоит из всех точек (x, y, z), для которых 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 и 0 ≤ z ≤ 1. Чтобы найти все части границы куба C, так же, как и в случае с квадратом, зафиксируем одну из координат в своем крайнем значении 0 или 1 и позволим оставшимся двум координатам изменяться на всем интервале [0,1]. Так мы видим, что граница куба состоит из шести граней, каждая из которых представляет собой квадрат.

левая грань x = 0, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1

правая грань x = 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1

нижняя грань y = 0, 0 ≤ x ≤ 1, 0 ≤ z ≤ 1

верхняя грань y = 1, 0 ≤ x ≤ 1, 0 ≤ z ≤ 1

передняя грань z = 1, 0 ≤ y ≤ 1, 0 ≤ x ≤ 1

задняя грань z = 0, 0 ≤ y ≤ 1, 0 ≤ x ≤ 1

Единичный гиперкуб H в координатном пространстве wxyz состоит из всех точек (w, x, y, z), для которых 0 ≤ w ≤ 1, 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 и 0 ≤ z ≤ 1. Чтобы найти все части границы гиперкуба H, зафиксируем одну из координат в своем крайнем значении, а оставшиеся три координаты пусть изменяются в пределах интервала [0,1]. К примеру, один из граничных кубов задается условиями:

w = 0, 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1.

У каждой координаты есть два крайних значения, поэтому наличие четырех координат означает, что граница гиперкуба состоит из восьми кубов. Эти восемь кубов представлены на рисунке ниже. На двух верхних изображениях мы затеняем два «очевидных» куба. Назовем затененный куб слева нижним кубом, а затененный куб справа – верхним кубом.

Каждый из остальных шести затененных кубов соединяет одну из граней нижнего куба с соответствующей гранью верхнего куба.

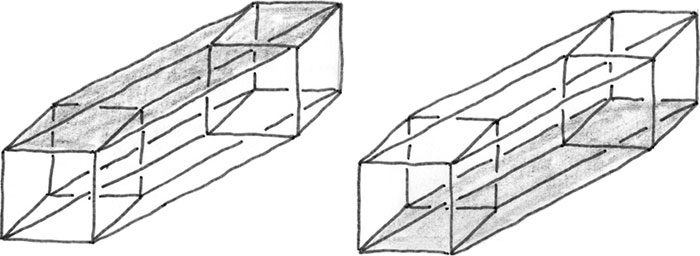
Например, левый затененный куб во втором ряду соединяет верхнюю грань нижнего куба с верхней гранью верхнего куба.

Из скольких гиперкубов состоит граница пятимерного куба?

ПОЧЕМУ √2 – ИРРАЦИОНАЛЬНОЕ ЧИСЛО?

Чтобы показать, что квадратный корень из 2 не является отношением двух целых чисел, мистер Гриффит рассуждал так. Предположим, что можно записать √2 в виде отношения целых чисел, скажем, √2 = a/b, и пусть эта дробь несократима (так, например, вместо ¹⁴/₁₀ мы возьмем 7/5). Теперь возведем обе части в квадрат и получим 2 = a²/b², откуда 2b² = a². Каким является число a², четным или нечетным? Оно четное, поскольку равно удвоенному числу b². Тогда каким является само число a, четным или нечетным? Ну раз квадрат четного числа всегда четен, а квадрат нечетного числа всегда нечетен, значит, число a должно быть четным. Это означает, что a = 2c для некоторого целого числа c. Теперь вернемся к равенству 2b² = a². Видите, в чем проблема? Хм, 2b² = a² = (2c)² = 4c². Теперь поделим эти равенства на 2. Что мы видим? Оказывается, b² = 2c², откуда b² – четное число, значит, и b – четное число, но в этом-то и проблема, что оба числа a и b – четные, а мы взяли несократимую дробь a/b. Ха, как здорово.

О ФРАКТАЛАХ МЕЛКИМ ШРИФТОМ

Когда мы говорим, что треугольник Серпинского – единственная фигура, не изменяемая при применении к ней правил треугольника, надо проявить некоторую осторожность. Треугольник Серпинского не является единственной такой фигурой. Например, если применить три правила треугольника ко всей плоскости, то в результате мы снова получим всю плоскость. Зато можно утверждать, что треугольник Серпинского – единственная замкнутая и ограниченная фигура, которая не изменяется при применении к ней всех трех правил треугольника.

Фигура называется замкнутой, если ее дополнение – открытая фигура, а открытой называется фигура, каждая точка которой является центром небольшого круга, лежащего целиком внутри этой фигуры. К примеру, фигура {(x, y): x² + y² < 1} является открытой, а {(x, y): x² + y² ≤ 1} таковой не является.

Фигура называется ограниченной, если ее можно заключить внутри окружности достаточно большого радиуса.

НЕМНОГО О ФРАКТАЛЬНОЙ РАЗМЕРНОСТИ

В этом разделе гораздо больше математики, чем в остальных главах книги. Здесь мы вкратце обрисуем геометрию размерностей, о которой уже говорилось в пятой главе. Не будем выходить за рамки простой геометрии; в реальном мире всё сложнее из-за присущей природе зашумленности. Мы начали говорить о размерности, задавшись вопросом: сколько копий некоторой фигуры возникнет, если удвоить ее ширину и высоту? Но будет еще проще обобщить другой, связанный с этим подход. Вместо того чтобы увеличивать фигуру, мы оставим ее прежние размеры и попытаемся разбить ее на более мелкие копии, подобные целой фигуре. Мы уже рассматривали такую декомпозицию для треугольника Серпинского: он состоит из трех своих копий, масштабированных с коэффициентом 1/2. Обозначим число копий как N, а коэффициент подобия – как r. Тогда фрактальная размерность d будет задаваться соотношением

N = (1/r)^d.

Почему здесь стоит 1/r? Потому что N больше 1, а r меньше 1, и, по крайней мере, в этих условиях d является положительным числом. Чтобы найти d, возьмем логарифм от обеих частей равенства, используем известную из алгебры формулу log((1/r)^d) = d log(1/r) и разрешим уравнение относительно d:

В основе этого вычисления лежит предположение о самоподобии фигуры, поэтому d называется размерностью подобия. Для треугольника Серпинского размерность подобия равна

Предположим, что фигура самоподобна, но коэффициенты подобия ее частей неодинаковы. Возможно, каждая из N частей имеет свой коэффициент подобия, r₁,…, r_N.

Формула для вычисления размерности подобия не позволяет включить более одного коэффициента подобия. Но мы можем записать выражение N = (1/r)^d в виде

Nr ^d = 1, то есть r ^d +… + r^d = 1,

где r ^d +… + r^d – это N слагаемых

Поскольку теперь у нас есть свое слагаемое для каждого коэффициента подобия, то в этом уравнении для размерности подобия найдется место для различных коэффициентов:

r₁d +… + r_Nd = 1.

Это так называемое уравнение Морана.

Например, здесь мы видим фрактал с различными коэффициентами подобия. Как показано на схематическом изображении справа, в этом фрактале

r₁ = r₂ = r₃ = 1/2,

r₄ = r₅ = 1/4,

и поэтому уравнение Морана принимает вид

3(1/2) ^d + 2(1/4) ^d = 1.

Можно подумать, что это уравнение необходимо решать численно, поскольку мы не можем разрешить его относительно d, взяв логарифм от обеих частей равенства. Но в данном случае есть другая возможность, поскольку (1/4) ^d = ((1/2)²) ^d = ((1/2) ^d)².

Путем введения обозначения (1/2) ^d = x уравнение Морана приводится к квадратному уравнению

3 x + 2 x ² = 1.

Применив формулу для корней квадратного уравнения, мы находим x = (−3 ± √17)/4. Поскольку x = (1/2) ^d – положительное число, мы берем x = (3 + √17)/4. Наконец, чтобы найти значение d, вычислим логарифм от обеих частей равенства

и найдем отсюда d:

Укажем здесь два видоизменения рассмотренной ситуации, хотя существуют и многие другие. Все результаты взяты из нескольких источников, все они собраны в шестой главе моей книги «Фрактальные миры: как их выращивать, выстраивать, воображать»^[133].

Сначала рассмотрим случайные фракталы. Это значит, что вместо применения одних и тех же коэффициентов подобия на каждой итерации построения фрактала каждый коэффициент подобия может теперь принимать одно из нескольких значений с заданными вероятностями. В этом случае уравнение Морана выглядит так:

E (r_i^d) +… + E (r_N^d) = 1,

где E (r_i^d) – среднее значение величины r_N^d – среднее значение величины. Назовем это стохастическим уравнением Морана.

На рисунке со следующей страницы – случайный фрактал, состоящий из N = 4 частей, каждая из которых имеет коэффициент подобия r = 1/2 с вероятностью 1/2 и r = ¼ с вероятностью 1/2. Тогда для каждой части среднее значение задается формулой

E (r_i^d) = 1/2 (1/2) ^d + 1/2 (1/4) ^d.

Снова введем обозначение x = (1/2) ^d, тогда

x² = (1/4) ^d. После чего стохастическое уравнение Морана превращается в квадратное уравнение 2x + 2x² = 1, откуда получаем размерность

Но что это за число? Разумеется, различные последовательности выбора коэффициентов 1/2 и ¼ дадут нам разные случайные фракталы. Вычисленная нами размерность является средним значением размерностей, которые мы могли бы получить, если бы по тому же алгоритму сгенерировали много фракталов.

Наконец, вернемся к фракталу, изображенному в первой главе. Он получен при помощи четырех преобразований с одинаковыми коэффициентами подобия r = 1/2, но при этом разрешены лишь некоторые их комбинации.

Чтобы это выразить, можно, например, обозначив квадранты фрактала метками 1 (нижний левый), 2 (нижний правый), 3 (верхний левый) и 4 (верхний правый). Разрешенные и запрещенные комбинации можно закодировать в виде матрицы. Порядковый номер строки задает квадрант, а порядковый номер столбца – субквадрант этого квадранта. Например, значение в первой строке и втором столбце соответствует нижнему правому субквадранту внутри нижнего левого квадранта. Число 0 в матрице означает, что соответствующий субквадрант не занят, а число 1 – занят. Тогда матрица, кодирующая показанный выше фрактал, имеет вид

Поскольку все коэффициенты подобия равны r = 1/2, мы получаем уравнение

(1/2) ^d ρ[M] = 1,

которое можно назвать уравнением Морана с памятью.

Множитель ρ[M] называется спектральным радиусом M. Это наибольшее собственное значение матрицы M. Мы не станем здесь объяснять, как вычисляются собственные значения.

Загляните в любую книгу по линейной алгебре или в Приложения А.83 и А.84 «Фрактальных миров». Для нашей матрицы M собственными значениями являются числа 1±√3, 1 и 1. Количество собственных значений равно числу строк (или столбцов) матрицы, при этом некоторые собственные значения могут повторяться, как в нашем примере собственное значение 1. Спектральный радиус равен ρ[M] = 1 + √3, и, решив уравнение Морана с памятью относительно d, мы получаем

Можно перечислить еще много видоизменений уравнения Морана. Например, есть версия уравнения Морана для случая, когда коэффициент подобия изменяется в зависимости от положения аргумента преобразования. Но нам пока этого достаточно.

Последнее замечание об уравнении Морана. В некоторых из наших примеров мы сводили его к квадратному уравнению. А что делать, если в результате решения квадратного уравнения мы получим комплексное число? Такого просто не может быть: уравнение Морана всегда имеет решение, причем только одно. См. Приложение А.76 «Фрактальных миров».

А теперь кое-что мелким шрифтом об измерении и размерности.

Если мы попытаемся найти меру фигуры при помощи некоторого объекта размерности меньше, чем размерность этой фигуры, то в ответе мы получим ∞; если же мы проводим измерение при помощи объекта размерности большей, чем размерность исходной фигуры, то в ответе получим 0. Расчеты здесь довольно сложные, но можно проиллюстрировать саму идею на следующем примере. Возьмем в качестве фигуры заполненный единичный квадрат – он, несомненно, двумерен.

Представьте, что для измерения его длины мы пытаемся покрыть квадрат бесконечно тонкой нитью. Такая нить любой конечной длины оставит много непокрытых участков, поэтому для покрытия квадрата нужна нить бесконечной длины.

С другой стороны, квадрат помещается в коробку с основанием в форме единичного квадрата и высотой h для любого h > 0. Объем такой коробки V = 1²h = h. По мере того как мы берем всё меньшие значения h, объем коробки приближается к нулю, поэтому объем квадрата равен 0.

А вот теперь то, что написано мелким шрифтом: мы будем рассматривать только ограниченные фигуры. Бесконечно длинная, но узкая полоса на плоскости имеет бесконечную площадь, но является двумерной. Получение бесконечного значения при измерении может быть обусловлено измерением при помощи объекта слишком малой размерности (этот случай нас интересует) или измерением неограниченной фигуры (этот случай нас не интересует). Поэтому остановимся на ограниченных фигурах.

Если пока всё описанное было слишком абстрактно, конкретизируем наши рассуждения на примере треугольника Серпинского. Предположим, что мы строим его на основе прямоугольного равнобедренного треугольника с основанием и высотой равными 1. Вспомним, что площадь треугольника равна 1/2 × основание × высоту, поэтому наш треугольник имеет площадь 1/2. Будем строить треугольник Серпинского другим способом – таким, который позволит легко подсчитать его площадь. Порядок таков: соединим середины сторон заполненного треугольника и удалим получившийся средний треугольник. В результате получим три заполненных треугольника, повторим эту процедуру для каждого из них и так далее.

Мы видим, что исходный (заполненный) треугольник представим в виде объединения треугольника Серпинского и семейства (заполненных) треугольников. Наибольший из этих удаленных треугольников имеет основание и высоту 1/2, поэтому его площадь равна ⅛. Следующие по величине удаленные нами треугольники (их три) имеют основание и высоту ¼, поэтому площадь каждого из них равна ¹/₃₂. Продолжая в том же ключе, мы можем вычислить сумму площадей всех удаленных треугольников:

Здесь в предпоследнем равенстве мы использовали формулу суммы геометрической прогрессии: для любого знаменателя r при |r| < 1 ряд 1 + r + r² + r³ + … сходится к величине 1/(1 – r). Площади удаленных треугольников в сумме равны 1/2, то есть площади исходного треугольника, поэтому площадь треугольника Серпинского равна 0.

Что мы можем понимать под длиной треугольника Серпинского? Первым делом стоит обратить внимание на сумму периметров треугольников. Периметр треугольника Серпинского, возможно, имеет части, которые мы не видим, а может быть, и нет, но давайте посмотрим, о чем нам говорят периметры видимых треугольников. Периметр большого прямоугольного треугольника равен 1 + 1 + √2 = p. Периметр первого удаленного треугольника равен p/2, периметры треугольников, удаленных во вторую очередь, равны p/4 и так далее. Тогда сумма этих периметров равна

Треугольник Серпинского является ограниченным множеством на плоскости с бесконечной длиной, поэтому его размерность > 1, а так как у него нулевая площадь, поэтому его размерность < 2. Поскольку размерность треугольника Серпинского лежит между двумя последовательными целыми числами, она сама не может являться целым числом. Вот так измерения могут сообщить нам что-то о размерности.

Благодарности

Любовь несомненно дороже, чем возможность утраты.

Прежде всего я должен поблагодарить мою тетю Рут Фрейм. Человек невероятно любопытный, она была тем взрослым, кто по-настоящему прислушивался к детским идеям. Она стала первой из тех, кого я потерял. Я был достаточно большим, чтобы понять, что произошло, но еще недостаточно, чтобы переварить слова взрослых о смерти. Когда она умерла, я почувствовал эту утрату в лоб, без прикрас. Это было чистое, парализующее чувство.

Но помимо боли утраты, то, что оказало гораздо большее влияние на выбор моего жизненного пути, была манера, с которой Рути будоражила мое любопытство, показывала мне, что наука – это дорога, на которой даже маленький ребенок может сделать первые шаги. Как бы я хотел, чтобы она увидела, какими стали ее племянницы и племянники. Как бы мне хотелось подарить ей свои книги «Хаос под контролем» и «Фрактальные миры» и сказать, что они стали итогом жизни, которую она когда-то мне показала^[134].

Мои родители, Мэри и Уолтер Фрейм; сестра и брат, Стив Фрейм и Линда Риффл, и их супруги Ким и Дэвид; мой племянник Скотт Лотес и его жена Морин Малдун; мой двоюродный брат Мэтт Эрроувуд, его жена Сьюзан и их сыновья Зейн и Уилл; а также я с моей женой Джин Маатта – все мы замысловатым образом сплели наши жизни воедино. Конечно, скорбь является частью жизни каждого из нас, но далеко не только она. Даже в самые плохие дни бывают светлые моменты. И даже в самые лучшие дни, эх…

Пространство повествования возникло в многочисленных беседах с Амелией Урри еще до того, как мы начали работу над «Фрактальными мирами». Восхитительное независимое исследование, проведенное совместно с Кэролайн Каннер и Кэролайн Сидни, заставило нас кое-что подправить в пространстве повествования и осветить множество других аспектов геометрии и литературы. Они стали основой наших рассуждений в четвертой главе.

Выстраиванию особых связей между пространством повествования и скорбью весьма способствовали содержательные и энергичные дискуссии с Ричем и Кайлой Мальюла. Рич – наш ветеринар. Он лечил и продолжает с удивительной заботой лечить наше кошачье семейство.

Мой племянник Скотт указал мне на геометрию сюжета в книге Джона Макфи «Черновик № 4»^[135]. Кроме того, мы со Скоттом много обсуждали книги Мураками. Два вдумчивых читателя с двумя разными подходами к любимому автору: я читаю его как геометр и преподаватель, а Скотт – как писатель, фотограф и издатель, – мы оба способны почерпнуть из сложного сюжета весьма несхожие, но одинаково ценные идеи.

Лара Санторо поделилась со мной своими мыслями о скорби. Поскольку она много лет работала иностранным корреспондентом, писала об эпидемии СПИДа в Найроби, ее непосредственный опыт скорби представляет большую ценность. В романе «Милосердие» она в художественной форме описывает эту часть своей жизни; а в романе «Мальчик» рассказывает об ином типе скорби, затрагивающем сложные нравственные темы^[136]. В нашей переписке и беседах Лара поведала о своем методе «широкого объектива», который помогает справляться со скорбью. Если вам удается посмотреть на собственные мысли как бы со стороны, скорбь несколько утрачивает свою силу. Эта идея изменила ход моих рассуждений в пятой главе.

В переписке с Андреа Слоун Пинк мы обсуждали жизненные истории, утраты и наше восприятие мира. Мы с Андреа начали обмениваться электронными письмами после того, как я обнаружил, что являюсь персонажем одной из ее пьес^[137]. Мать Андреа умерла вскоре после смерти моего отца. В беседах о том, как мы скорбим об утрате близкого человека, обнаружились некоторые различия в нашей манере скорбеть. Эта переписка была очень содержательной и, по крайней мере для меня, весьма утешительной.

Мой издатель Джо Каламия обрисовал идею этой книги на основе разговора, который состоялся между нами много лет назад. Это третий наш совместный проект; работа с Джо – ни с чем не сравнимое удовольствие. Данная книга – мой первый неакадемический текст. Джо деликатно, терпеливо и неутомимо подсказывал мне, как сделать книгу более понятной широкой аудитории. Благодаря Джоэлу Скору, который внимательно вычитал текст, и его обстоятельным замечаниям я смог увидеть свой поток идей в представлении читателя. Его мастерство – еще одна причина, почему мне нравится работать с издательством Университета Чикаго. Надеюсь, у нас втроем еще будут совместные проекты.

Моя двоюродная сестра Патти Рейд прочла рукопись, нашла пропущенные мной опечатки и сделала полезные замечания относительно моего тона. А еще она подарила мне фотографию, где мы сидим с ней за столом на кухне и травим байки: эта картинка держала меня на плаву в трудные времена. Да, семья – это важно. Кроме того, Патти познакомила меня со своими внуками Астериск (Астрид) и БитлБомб (Айра): их любопытство и умение радоваться миру – еще одно доказательство того, что любовь несомненно дороже, чем возможность утраты.

Майк Доналли, единственный из огромного числа моих соседских друзей детства, с кем мы поддерживаем связь, рассказал множество фактов о тех временах, которые улетучились из моей памяти. Спасибо, Майк.

Пол Данкл, некогда мой одноклассник, а теперь член семьи и друг, тоже сообщил мне несколько важных фактов о том времени. Спасибо, Пол.

Немаловажную техническую поддержку в подготовке этой и трех моих предыдущих книг оказал мне Энди Шимковяк. Спасибо, Энди.

В ноябре 2012 года я участвовал в одной секции с Лори Сантос. Секция, организованная группой студентов, началась с дискуссии о счастье, но вскоре под напором студенческих вопросов перекинулась и на другие темы. Когда кто-то из зала задал вопрос о депрессии, Лори предоставила слово мне, хотя, я уверен, она могла бы сказать что-то более интересное. Пока я отвечал на вопрос, у меня блеснула мысль, что геометрия может пролить свет на наши чувства. Идея этой книги выросла из той мимолетной мысли, которую я затем держал в голове во время разговора с Джо Каламия. Спасибо, Лори, за то, что предоставила мне возможность развить мысль, которая на тот момент едва проклевывалась.

Вдумчивые и подробные комментарии двух анонимных рецензентов привели к существенным улучшениям в плане организации и представления идей. Один из рецензентов указал мне на книгу Джона Аллена Паулоса «Математика и юмор», но не потому, что в скорби есть что-то смешное, а потому, что в пятой главе Паулос развивает геометрическую теорию юмора^[138]. Это помогло мне доработать некоторые аспекты своей геометрической теории скорби. Кроме того, ободряющие замечания обоих рецензентов помогли мне справиться с тревогой о том, будет ли моя книга кому-то интересна. Рецензенты могут оказать существенное влияние на продвижение автором своего проекта.

Беседы с моей женой Джин Маатта, ее доброта и терпение стали неоценимым вкладом в эту и другие написанные мной книги. Если я проживу еще тридцать лет (что маловероятно: вряд ли я дотяну до ста), то лишь тогда, вероятно, пойму, как мне повезло, что она согласилась выйти за меня замуж.

Потеря многих питомцев раскрыла передо мной новые масштабы скорби и помогла направить в нужное русло некоторые из идей данного проекта. Но в то же время тысячи часов, когда кот засыпал у меня на коленях, пока я работал, были для меня невероятно счастливыми. И я ни за что не променял бы это счастье ради того, чтобы не чувствовать боли от их утраты.

Скорбь – часть нашей жизни. Можно ли с помощью геометрии уменьшить нашу боль, вызванную скорбью? Как вы думаете?

* * *

Фотография Рут Фрейм в начале раздела со словами благодарности взята из старого семейного альбома. Все, кто могли помнить фотографа, давно умерли. Фотография Астериск и БитлБомб сделана Джоном Кимом.

Компьютерные изображения были созданы мной с помощью системы Mathematica. Даже если вам показалось, что рисунки от руки выполнены моим десятилетним родственником, увы, они сделаны мной. Что ж, ведь за последние шестьдесят лет мои навыки рисовальщика не совершенствовались. Всё это время я изучал математику, физику, программирование и немного биологию, но, к сожалению, не изобразительное искусство.

Примечания

1

1. «Хуже», ведь, во что бы вы ни верили, отрицание утраты порочит память о жизни покойного. Даже маленькие дети достойны того, чтобы с ними говорили честно, пусть эта честность будет немного отфильтрованной и смягченной, но всё же останется честностью. Скажите детям: печалиться – нормально; никогда не говорите им, что не бывает причин для грусти.

(обратно)

2

1* Здесь и далее цифрами обозначены примечания автора, астерисками – примечания редактора.

(обратно)

3

2* Этан Канин (род. 1960) – американский писатель, педагог и врач.

(обратно)

4

2. Моя дорогая приятельница Кристин Уолдрон подарила мне книгу Этана Канина «Альманах для сомневающихся» (Canin E. A Doubter’s Almanac. New York: Random House, 2016). Многие годы я читал работы Канина и восхищался ими. Кристин подвела меня к этой книге раньше, чем я сам бы до нее добрался – на самом деле, это случилось вскоре после смерти отца, которая, очевидно, повлияла на мое восприятие слов Канина.

(обратно)

5

3* Дословно: «Если бы не неудача, то и удачи

(обратно)

6

3. Книги Джона Арчера (Archer J. The Nature of Grief. New York: Taylor & Francis, 1999) и Барбары Кинг (King B. How Animals Grieve. Chicago: University of Chicago Press, 2014) являются прекрасной отправной точкой для глубоких размышлений на тему скорби. Книга Кинг более повествовательная, более личная; книга Арчера трактует тему более абстрактно. В этом смысле обе работы дополняют друг друга, обе познавательны. Во второй главе «Природы скорби» дан исторический обзор исследований по теме скорби. В своей статье «Эволюционные основы для понимания скорби» (Nesse R. An Evolutionary Framework for Understanding Grief / ed. D. Carr, R. Nesse, C. Wortman // Spousal Bereavement in Late Life. New York: Springer, 2005. P. 195–226) Рэндольф Несси дает нам четкое объяснение эволюционного происхождения скорби в контексте своей новаторской работы по эволюционной медицине, написанной совместно с Джорджем Уильямсом (см.: Nesse R., Williams G. Why We Get Sick: The New Science of Darwinian Medicine. New York: Random House, 1994).

(обратно)

7

4* Александр Шенд (1858–1936) – английский писатель, адвокат, один из основателей Британского психологического общества.

(обратно)

8

4. Книга Александра Шенда «Основы характера» (Shand A. The Foundations of Character. London: Macmillan, 1914) является первым систематическим исследованием скорби.

(обратно)

9

5. В третьей главе «Природы скорби» Арчер исследует скорбь сквозь призму искусства.

(обратно)

10

6. Эти книги Жан-Поля Сартра дали мне первое и самое ясное на сегодняшний день представление о литературе как о наиболее прямом пути к глубоким истинам. Сартр тщательно анализирует эту тему с точки зрения философии в книге «Бытие и ничто: опыт феноменологической онтологии». Правда, подзаголовок книги не слишком вдохновляет. В цикле романов «Дороги свободы» («Возраст зрелости», «Отсрочка» и «Смерть в душе») рассказы персонажей приводят к схожему пониманию. Их истории вызывают отклик.

(обратно)

11

7. Музыка придает звучание, чувство, кристально выверенное придыханием в голосе и подчеркнутое ритмом. Потом к ней иногда добавляется задумчивый фортепианный монолог, ансамблевые инструменты или сложная сеть людских голосов, наслаивающихся друг на друга. Порой звук взмывает ввысь, то дополняя, то заглушая поэзию текста. Благодаря музыке мы можем прочувствовать всю многокрасочность жизни более непосредственно и более многослойно, чем представляет нам текст. Вот несколько примеров: Натали Мерчант, «My Skin» с альбома «Ophelia» (Elektra, 1998) и «Beloved Wife» с альбома «Tiger Lily» (Elektra, 1995); Лорина Маккеннитт, «Dante’s Prayer» с альбома «The Book of Secrets» (Quinlan Road, 1997); Филип Гласс, «Сочленение № 5» из оперы «Эйнштейн на пляже» (Elektra, 1993). Я мог бы назвать еще десятки, если не сотни композиций. Как и вы. Интересно, чей список был бы длиннее?

(обратно)

12

5* Йо Йо Ма (род. 1955) – известный американский виолончелист китайского происхождения, композитор.

(обратно)

13

8. Великолепный фильм Энга Ли «Крадущийся тигр, затаившийся дракон» («Коламбия Пикчерз», 2000) завершается захватывающим (в буквальном смысле слова – во всяком случае, у меня перехватило дыхание, и, судя по приглушенным всхлипываниям, я был не один такой в зале) «Прощанием» в исполнении Йо Йо Ма.

(обратно)

14

9. Песня Сии «Breathe Me» из альбома «Color the Small One» (Astralwerks, 2006).

(обратно)

15

10. Родители не должны переживать своих детей. Задолго до смерти родителей младший брат моей мамы, Билл, умер от рака легкого – результат выкуривания двух пачек сигарет в день на протяжении сорока лет. Скорбь его родителей была еще горше, потому что они пытались держать себя в руках. Но кто в таком случае может держать себя в руках? В «Отцах и детях» Тургенев описывает скорбь родителей Евгения просто, без прикрас и трогательно. По-настоящему трогательно.

(обратно)

16

11. Первым широко известным исследованием на тему скорби стала статья Эриха Линдеманна «Клиника острого горя» (Lindemann E. Symptomatology and Management of Acute Grief // American Journal of Psychiatry. Vol. 101. 1944. P. 141–148. Рус. пер.: Линдеманн Э. Клиника острого горя [1944] / под ред. В. К. Вилюнаса, Ю. Б. Гиппенрейтер // Э. Линдеманн. Психология эмоций. М.: Изд-во Моск. ун-та, 1984). Линдеманн включил в свой анализ так называемое предвосхищающее горе, подразумевая эмоциональную реакцию того, кто боится потерять любимого человека. Это единственное исключение из строгого правила о необратимости скорби.

(обратно)

17

6* Бранко Грюнбаум (1929–2018) – израильский и американский математик, один из создателей теории абстрактных многогранников.

(обратно)

18

7* Джоффри Шепард (1927–2016) – английский математик, доктор философии Бирмингемского университета.

(обратно)

19

1. Grünbaum B., Shephard G. Tilings and Patterns. New York: Freeman, 1987.

(обратно)

20

2. Доказательство того, что существует ровно семнадцать групп орнаментов, было представлено в статье: Фёдоров Е. С. Симметрия на плоскости // Записки Императорского Санкт-Петербургского Минералогического общества. Т. 28. СПб.: Типография Императорской Академии Наук, 1891. С. 345–390. Зачем нам нужно это доказательство? Не будь его, оставалась бы вероятность, что существует некая восемнадцатая группа орнаментов (узор замощения, предлагающий новую форму мозаики), скрывающаяся где-то в складках геометрии и доселе оставшаяся незамеченной.

(обратно)

21

3. Собор Благовещения Святой Марии в городе Ананьи (Италия) был построен в 1104 году. Внутренняя мозаика, включая узор из треугольников Серпинского, показанный на рисунке в тексте, была добавлена столетием позже. Этьен Гийон и Юджин Стэнли (Guyon E., Stanley H. E. Fractal Forms. Haarlem: Elsevier, 1991) привлекли внимание к фрактальным элементам мозаики. См. фото на: https://commons.wikimedia.org/wiki/File: Anagni_katedrala_04.JPG

(обратно)

22

4. Лучшее изображение картины «Лицо войны» вы можете увидеть в Википедии (https://en.wikipedia.org/wiki/The_Face_of_War) или на с. 97 книги Робера Дешарна «Дали» (Descharnes R. Dalí. New York: Abrams, 1985), которая также включает предварительный анализ этой картины.

(обратно)

23

5. Видеоролик «Линейная перспектива: эксперимент Брунеллески» (https://www.youtube.com/watch?v=bkNMM8uiMww) демонстрирует данный эксперимент с зеркалом.

(обратно)

24

6. Книга Банхоффа «По ту сторону третьего измерения: геометрия, компьютерная графика и высокая размерность» (Banchoff T. Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions. New York: Freeman, 1990) могла бы называться «Тринадцать способов увидеть гиперкуб» (прошу прощения у Уоллеса Стивенса и у Генри Луиса Гейтса мл.).

(обратно)

25

7. Источники изображения картины Дали «Распятие. Гиперкубическое тело»: Википедия (https://en.wikipedia.org/wiki/Crucifixion_(Corpus_Hypercubus)); книга Банхоффа «По ту сторону третьего измерения», с. 105; и книга Дешарна «Дали», с. 119. В книге Банхоффа на с. 110 есть фотография, на которой Банхоффа разговаривает с Дали.

(обратно)

26

8. Хорошие работы по неевклидовой геометрии: Coxeter H. S. M. Non-Euclidean Geometry, 5^th ed. Toronto: University of Toronto Press, 1965; Greenberg M. Euclidean and Non-Euclidean Geometries: Development and History, 4^th ed. New York: Freeman, 2007. Статья в Википедии (https://en.wikipedia.org/wiki/Non-Euclidean_geometry) также может стать неплохой отправной точкой. А на странице https://brewminate.com/escher-and-coxeter-a-mathematical-conversation/ рассказывается о переписке Маурица Эшера и Гарольда Коксетера.

(обратно)

27

9. Репродукции «Предела круга III» Эшера можно найти на Википедии https://en.wikipedia.org/wiki/Circle_Limit_III и в книге Esher M. C. M. C. Esher: 29 Master Prints. New York: Abrams, 1983.

(обратно)

28

8* Гарольд Коксетер (1907–2003) – канадский математик британского происхождения. Считается одним из крупнейших геометров XX века.

(обратно)

29

9* Шон Кэрролл (род. 1966) – американский физик-теоретик и космолог. Специализируется на исследованиях темной энергии и общей теории относительности.

(обратно)

30

10. Carroll S. Something Deeply Hidden: Quantum Worlds and the Emergence of Spacetime. New York: Dutton, 2019. Рус. пер.: Кэрролл Ш. Квантовые миры и возникновение пространства-времени [2021] / пер. О. Сивченко. СПб.: Питер, 2022.

(обратно)

31

11. Некоторые подробности и дополнительные примеры фракталов, созданных с помощью памяти, приведены в разделе 2.5 книги Майкла Фрейма и Амелии Урри «Фрактальные миры» (Frame M., Urry A. Fractal Worlds: Grown, Built, and Imagined. New Haven, CT: Yale University Press, 2016).

(обратно)

32

12. Это доказательство, известное как «Теорема Гёделя о неполноте», было настолько неожиданным, а сама идея, лежащая в его основе, настолько гениальной, что Курт Гёдель и Альберт Эйнштейн стали часто прогуливаться вместе по территории Института перспективных исследований в Принстоне. Эйнштейн заметил, что стал чаще захаживать в свой кабинет «только ради чести прогуляться до дома с Куртом Гёделем». История их дружбы прекрасно рассказана в книге Джима Холта «Идеи с границы познания: Эйнштейн, Гёдель и философия науки» (Холт Дж. Идеи с границы познания: Эйнштейн, Гёдель и философия науки [2018] / пер. А. Бродоцкой. М.: АСТ, 2019. С. 13); именно из нее я процитировал слова Эйнштейна. Книга Эрнеста Нагеля и Джеймса Ньюмена «Теорема Гёделя» (Нагель Э., Ньюмен Дж. Теорема Гёделя [1958] / пер. Ю. А. Гастева. М.: КРАСАНД, 2009) дает ясное и компактное объяснение Теоремы Гёделя о неполноте. А поразительная книга Дугласа Хофштадтера «Гёдель, Эшер, Бах: эта бесконечная гирлянда» (Хофштадтер Д. Р. Гёдель, Эшер, Бах: эта бесконечная гирлянда [1979] / пер. М. А. Эскиной. Самара: Бахрах-М, 2001) представляет заметно более развернутое и невероятно увлекательное объяснение теоремы Гёделя, где каждая глава предваряется оригинальной притчей об Ахилле, черепахе и их друзьях.

(обратно)

33

13. Доказательство того, что эти три классические задачи греческой геометрии не могут быть решены, пользуется так называемой теорией Галуа: данный раздел математики наглядно представлен в книге Иэна Стюарта «Теория Галуа» (Stewart I. Galois Theory, 2^nd ed. London: Chapman and Hall, 1973). С помощью искусных аргументов эти три геометрические задачи превращаются в алгебраические конструкции, а затем показывается, что они невозможны. Как ни удивительно, но некоторые из этих задач могут быть решены в неевклидовой геометрии.

(обратно)

34

14. Последовательность рисунков, объясняющих, как кот превращается в треугольник Серпинского, показана на странице 133. Вы поймете, когда увидите.

(обратно)

35

10* Джон Мьюр (1838–1914) – американский естествоиспытатель, писатель, защитник дикой природы.

(обратно)

36

11* Рейчел Карсон (1907–1964) – американский биолог, деятельница в сфере охраны природы, писательница.

(обратно)

37

12* Эдвард Эбби (1927–1989) – американский писатель, эссеист, активист-эколог.

(обратно)

38

13* Мартин Гарднер (1914–2010) – американский математик-любитель, писатель, популяризатор науки.

(обратно)

39

15. Гарднер М. Есть идея! [1978] / пер. Ю. А. Данилова. М.: Мир, 1982.

(обратно)

40

16. Борхес Х. Л. Лабиринты / пер. В. Кулагиной-Ярцевой, Е. Лысенко, И. Петровского, Б. Дубина, В. Багно. М.: АСТ, 2016. Эта книга, по-моему, лучше всего вводит в мир темпераментной фантазии Борхеса.

(обратно)

41

17. Например, Борхес написал рецензию на книгу Эдварда Казнера и Джеймса Ньюмена «Математика и воображение» (см. пер. Б. Дубина в сборнике: Борхес Х. Л. Зеркало загадок / пер. К. Корконосенко, Б. Дубина, Б. Ковалева, В. Багно. М.: КоЛибри, 2022).

(обратно)

42

18. Рассказ «Вавилонская библиотека» Борхеса и эссе «Аватары черепахи» являются прекрасными образцами парадоксов и головоломок.

(обратно)

43

19. Арифметика бесконечных чисел описана Борхесом на первых страницах его эссе «Учение о циклах» (см. пер. Е. Лысенко в сборнике: Борхес Х. Л. Лабиринты / пер. В. Кулагиной-Ярцевой, Е. Лысенко, И. Петровского, Б. Дубина, В. Багно. М.: АСТ, 2016).

(обратно)

44

20. Интересные вариации Борхес представляет в первом рассказе из сборника «Лабиринты» «Тлён, Укбар, Орбис Терциус».

(обратно)

45

21. Этот круг не настолько очевиден, как в романе Жозе Сарамаго «Перебои в смерти» (Сарамаго Ж. Перебои в смерти [2005] / пер. А. Богдановского. СПб.: Азбука, 2015), но тем не менее это круг. Короткий роман Сарамаго является прекрасным образцом сюжетной геометрии, представляющей собой замкнутый круг. Подробнее мы рассмотрим данный роман в третьей главе.

(обратно)

46

22. Борхес Х. Л. Циклическое время [1941] / пер. И. Петровского // Лабиринты. М.: АСТ, 2016. С. 109–113.

(обратно)

47

14* Здесь и далее цитируется пер. М. Былинкиной.

(обратно)

48

15* Макс Тегмарк (род. 1967) – шведско-американский космолог и астрофизик.

(обратно)

49

23. Насколько велико число 10¹⁰¹¹⁸? Число 10¹¹⁸ – это единица и 118 нулей, значит, 10¹⁰¹¹⁸ – это единица и 10¹¹⁸ нулей. Так уж ли это много? Количество частиц в наблюдаемой Вселенной равно примерно 10⁸⁰, то есть 10¹¹⁸ (заметим, это только количество нулей в нашем числе) равно количеству частиц в 10³⁸ копий наблюдаемой Вселенной.

(обратно)

50

24. Немного космологии. См. статью Макса Тегмарка «Параллельные Вселенные» (Tegmark M. Parallel Universes // Scientific American. Vol. 288. May 2003. P. 40–51) и его книгу о математизации космологии (Тегмарк М. Наша математическая Вселенная: В поисках фундаментальной природы реальности [2014] / пер. А. Сергеева. М.: АСТ, 2017). Основные идеи таковы: «Существует внешняя физическая реальность, полностью независимая от нас, людей» и «Наша внешняя физическая реальность является математической структурой». Это очень интересная книга.

(обратно)

51

25. Первые вычисления относительно того, как модель Большого взрыва может объяснить наблюдаемое в космосе изобилие наиболее легких элементов, были представлены в статье Ральфа Альфера, Ханса Бете и Георгия Гамова «Происхождение химических элементов» (Alpher R., Bethe H., Gamow G. The Origin of Chemical Elements // Physical Review. Vol. 73. 1948. P. 803–804). (Гамов, известный шутник, добавил фамилию «Бете» в авторы статьи, чтобы на нее ссылались как на статью Альфера-Бете-Гамова (α-β-γ). Это правда.) Гораздо подробнее и на основе более свежих астрономических данных этот вопрос освещен в статье Альфера «Истоки первичного нуклеосинтеза и предсказание космического фонового излучения» (Alpher R. Origins of Primordial Nucleosynthesis and Prediction of Cosmic Background Radiation / ed. N. Hetherington // Encyclopedia of Cosmology: Historical, Philosophical, and Scientific Foundations of Modern Cosmology. New York: Garland. 1993. P. 453–475).

(обратно)

52

26. Кэрролл Ш. Вечность: В поисках окончательной теории времени [2010] / пер. Е. Шикаревой. СПб.: Питер, 2016. Это кристально ясное размышление об истоках направленности времени. Что касается подхода Больцмана к проблеме низкой энтропии ранней Вселенной, см. рисунки на с. 213 и 216, а также текст, относящийся к данным рисункам. В десятой главе «Повторяющиеся кошмары» Кэрролл высказывает свои возражения против подхода Больцмана, а в пятнадцатой главе «Прошлое сквозь будущее» дает очень красивое объяснение своей теории о зародышах новых вселенных.

(обратно)

53

27. В «Личных заметках» (Ллойд С. Программируя Вселенную: Квантовый компьютер и будущее науки [2006] / пер. А. Стативки. М.: Альпина нон-фикшн, 2019) Сет Ллойд описывает, как однажды, когда он лазал по горам со своим другом Хайнцем Пагельсом, тот поскользнулся и, упав с крутой скалы высотой в несколько сотен метров, погиб. Ллойд вспомнил о модели множественности миров и подумал, что в каких-то, возможно даже во многих, вселенных его друг не упал. Это не принесло Ллойду облегчения. Андреа Слоан Пинк напомнила мне об этом эпизоде и сказала, что она и ее дети согласны с Ллойдом. Правда, далее Ллойд пишет: «Утешение постепенно приходило из информации – от битов, как реальных, так и воображаемых». Человек ушел, но его идеи и наша память о том, каким он был, какое-то время живут. Кроме того, Ллойд вспоминает о том, что как-то в Кембридже он встретил Борхеса и спросил писателя, навеян ли его рассказ «Сад расходящихся тропок» моделью множественности миров. Борхес ответил: «Нет». И добавил, что его не удивляет, когда законы физики отражают идеи, описанные в художественной литературе: в конце концов, физики тоже читают книги.

(обратно)

54

1. Определение хаоса, которое придумал Пуанкаре, когда пытался выяснить вопрос устойчивости Солнечной системы, приведено в его книге «Новые методы небесной механики» (Пуанкаре А. Новые методы небесной механики [1892] / сост. И. Б. Погребысского // А. Пуанкаре. Избранные труды в трех томах. Соч. в 3 т. Т. 1, 2. М.: Наука, 1971, 1972). Джордж Биркгоф и Жак Адамар открыли хаос в движениях на седловидных поверхностях: Birkhoff G. Quelques théorèmes sur le movement des systèmes dynamiques // Bulletin de la Société Mathématique de France. Vol. 40. 1912. P. 305–323; Hadamard J. Les surfaces à courbures opposes et leurs lignes géodésiques // Journal des Mathématiques. Vol. 4. 1898. P. 27–73. Люси Картрайт и Джон Литлвуд обнаружили хаос в динамике радарных цепей: Cartwright L., Littlewood J. On Non-Linear Differential Equations of the Second Order I: The Equation y′′ + k(1 – y²) + y = bλk cos(λt + a), k large // Journal of the London Mathematical Society s1-20. 1942. P. 180–189. Эдвард Лоренц открыл хаос в ранних компьютерных экспериментах с моделями атмосферной конвекции: Lorenz E. Deterministic Non-Periodic Flows // Journal of the Atmospheric Sciences. Vol. 20. 1963. P. 130–141. Роберт Мэй обнаружил хаос в простых моделях популяционной динамики с ограниченными ресурсами: May R. Simple Mathematical Models with Very Complicated Dynamics // Nature. Vol. 261. 1976. P. 459–467. В своей статье Мэй проводит анализ огромного количества работ по экспериментальной математике. Книга Джеймса Глика «Хаос. Создание новой науки» (Глик Дж. Хаос. Создание новой науки [1987] / пер. М. С. Нахмансона, Е. М. Барашковой. М.: Corpus, 2020) в популярной форме рассказывает об открытии хаоса.

(обратно)

55

16* Пуанкаре А. Наука и метод [1902] // А. Пуанкаре. О науке. М.: Наука, 1983. С. 323.

(обратно)

56

2. В своей книге «Исследуя скорбь» [так назывался первый перевод, сделанный Н. Трауберг для самиздата в 1970-х, позднее были выпущены новые переводы под названиями «Боль утраты» и «Исследуя горе»; см.: Льюис К. С. Настигнут радостью. Исследуя горе [1961] / пер. Л. Б. Сумм, С. Б. Лихачевой. М.: АСТ, 2022. – Примеч. пер. ] Клайв Льюис рассказывает о своей скорби после смерти жены.

(обратно)

57

3. См.: Дидион Дж. Год магического мышления [2005] / пер. Л. Сумм. М.: Corpus, 2021; Дидион Дж. Синие ночи [2011] / пер. В. Арканова. М.: Corpus, 2013. Потеряв менее чем за два года мужа и дочь, Дидион пережила в короткий срок неимоверное горе. А потом, спустя почти два года после смерти дочери, ее настиг опоясывающий лишай. Сколько страданий выпало ей одной.

(обратно)

58

17* Цит. по: Дидион Дж. Год магического мышления [2005] / пер. Л. Сумм. М.: Corpus, 2021.

(обратно)

59

18* Там же. С. 185

(обратно)

60

19* Там же. С. 186.

(обратно)

61

4. Heller P. The Dog Stars. New York: Knopf, 2012.

(обратно)

62

5. Поэтому, когда Эрих Линдеманн (Линдеманн Э. Клиника острого горя [1944] / под ред. В. К. Вилюнаса, Ю. Б. Гиппенрейтер // Э. Линдеманн. Психология эмоций. М.: Изд-во Моск. ун-та, 1984) и Колин Паркс (Parkes C. Anticipatory Grief // British Journal of Psychiatry. Vol. 138. 1981. P. 183) говорят об упреждающей скорби, я делаю для них исключение.

(обратно)

63

6. Archer J. The Nature of Grief. New York: Taylor & Francis, 1999. В шестой главе Арчер описывает, как он пытался найти низкоразмерные модели скорби. Его замечания, касающиеся фазового видения скорби, приведены на с. 100.

(обратно)

64

7. Bowlby J. Attachment and Loss, volume 3, Loss: Sadness and Depression. London: Hogarth, 1980.

(обратно)

65

8. Parkes C. Bereavement: Studies of Grief in Adult Life. London: Tavistock, 1972.

(обратно)

66

9. Shand A. The Foundations of Character. London: Macmillan, 1914.

(обратно)

67

10. Некоторые доводы против разложения скорби на стадии или фазы представлены в книге Арчера «Природа скорби».

(обратно)

68

11. Некоторые возражения против гипотезы о работе горя представлены в книге Арчера «Природа скорби», а также в статье: Stroebe M., Schut H. Does ‘Grief Work’ Work? // Bereavement Care. Vol. 22. 2009. P. 3–5.

(обратно)

69

21* Маргарет Штрёбе (род. 1946) – профессор кафедры клинической психологии и психологии здоровья Утрехтского университета, а также кафедры клинической психологии и экспериментальной психопатологии Гронингенского университета.

(обратно)

70

22* Хенк Шат (род. 1957) – доцент кафедры клинической психологии Утрехтского университета.

(обратно)

71

12. Штрёбе и Шат написали огромное количество работ о скорби. Модель двойного процесса была представлена в трех докладах на конференциях: Stroebe M., Schut H. Differential Patterns of Coping with Bereavement between Widows and Widowers // British Psychological Society Social Psychology Section Conference. Oxford: Jesus College, 22–24 September 1993; Stroebe M., Schut H. The Dual Process Model of Coping with Bereavement // Fourth International Conference on Grief and Bereavement in Contemporary Society. Stockholm, 12–16 June 1994; Stroebe M., Schut H. The Dual Process Model of Coping with Loss // International Work Group on Death, Dying and Bereavement. Oxford: St. Catherine’s College, 26–29 June 1995. Последние изменения были внесены в статье: Stroebe M., Schut H. The Dual Process Model of Coping with Grief: A Decade On // Omega. Vol. 61. 2010. P. 237–289.

(обратно)

72

13. Подробнее о родственном отборе можно почитать в перечисленных источниках: Bahar S. The Essential Tension: Competition, Cooperation, and Multilevel Selection in Evolution. New York: Springer, 2018; Hamilton W. D. The Genetic Evolution of Social Behavior, I and II // Journal of Theoretical Biology. Vol. 7. 1964. P. 1–52; Harman O. The Price of Altruism: George Price and the Search for the Origins of Kindness. New York: Norton, 2010; Nowak M., Highfield R. Supercooperators: Altruism, Evolution, and Why We Need Each Other to Succeed. New York: Simon & Schuster, 2011; Prum R. The Evolution of Beauty: How Darwin’s Forgotten Theory of Mate Choice Shapes the Animal World – and Us. New York: Doubleday, 2017; или посмотреть выступление Ричарда Прама на TEDxYale: https://www.youtube.com/watch?v=128-i8ulC7o

(обратно)

73

23* Patch (англ.) – глазная повязка, пятно неправильной формы.

(обратно)

74

24* Slinky (англ.) – шагающая пружинка (игрушка); to slink – идти крадучись.

(обратно)

75

14. King B. How Animals Grieve. Chicago: University of Chicago Press, 2014.

(обратно)

76

25* Джейн Гудолл (род. 1934) – британский приматолог, этолог и антрополог, посол мира ООН.

(обратно)

77

26* Синтия Мосс (род. 1940) – американский этолог, защитник и исследователь дикой природы, писатель.

(обратно)

78

27* Марк Бекофф (род. 1945) – американский биолог, этолог, поведенческий эколог и писатель.

(обратно)

79

15. Доказательства того, что у животных есть эпизодическая и автобиографическая память, представлены в статье: Martin-Ordas G., Bernsten D., Call J. Memory for Distant Past Events in Chimpanzees and Orangutans // Current Biology. Vol. 23. 2013. P. 1438–1441.

(обратно)

80

16. См., например, в книге Барбары Кинг «Как животные скорбят».

(обратно)

81

17. Этот факт описан в шестой главе книги Барбары Кинг «Как животные скорбят».

(обратно)

82

18. Макдональд Х. «Я» значит «ястреб» [2017] / пер. Н. Жутовской. М.: АСТ, 2017.

(обратно)

83

28* Цит. по: Макдональд Х. «Я» значит «ястреб» [2017] / пер. Н. Жутовской. М.: АСТ, 2017. С. 227.

(обратно)

84

29* Там же. С. 158.

(обратно)

85

30* Там же. С. 246.

(обратно)

86

19. «Эволюционная теория как основа для понимания скорби» была представлена Рэндольфом Несси в книге: Nesse R. An Evolutionary Framework for Understanding Grief / ed. D. Carr, R. Nesse, C. Wortman // Spousal Bereavement in Late Life. New York: Springer, 2005. P. 195–226.

(обратно)

87

20. Медицинские проблемы сквозь призму эволюционной теории исследуются на множестве примеров в книге Рэндольфа Несси и Джорджа Уильямса «Отчего мы болеем: эволюционная медицина как новая наука» (Nesse R., Williams G. Why We Get Sick: The New Science of Darwinian Medicine. New York: Random House, 1994).

(обратно)

88

1. Цитата взята из уже упомянутой книги Барбары Кинг «Как животные скорбят».

(обратно)

89

2. Позднее теории о красоте выдвигали Хьюм, Кант, Шопенгауэр и в особенности Сантаяна. Эстетика Сантаяны представлена в книге, основанной на его гарвардских лекциях с 1892 по 1895 год, «Чувство красоты» (Santayana G. The Sense of Beauty: Being the Outlines of Aesthetic Theory. New York: Scribner, 1896). Джон Тиммерман (Timmerman J. Robert Frost: The Ethics of Ambiguity. Lewisburg, PA: Bucknell University Press, 2002. P. 174) рассказывает, что Сантаяна написал эту книгу, которую он называл «паршивой халтурой», только чтобы сохранить свою должность в Гарварде.

(обратно)

90

3. Берлин написал книгу по эстетике, в которой он представляет свой тезис о «новизне и узнаваемости» (Berlyne D. Aesthetics and Psychobiology. New York: Appleton-Century-Crofts, 1971), и статью о человеческом любопытстве (Berlyne D. A Theory of Human Curiosity // British Journal of Psychology. Vol. 45. 1954. P. 180–191).

(обратно)

91

4. Сантаяна представляет свои доводы в пользу баланса чистоты и разнообразия в главе 16 книги «Чувство красоты».

(обратно)

92

5. См. книгу Дениса Даттона: Dutton D. The Art Instinct: Beauty, Pleasure, and Human Evolution. New York: Bloomsbury, 2009; и его лекцию на канале TED: https://www.ted.com/talks/denis_dutton_a_darwinian_theory_of_beauty?language=ru

(обратно)

93

6. Фильм «Крадущийся тигр, затаившийся дракон», реж. Энг Ли (Коламбия Пикчерз, 2000).

(обратно)

94

7. См.: Сарамаго Ж. Перебои в смерти [2005] / пер. А. Богдановского. СПб.: Азбука, 2015.

(обратно)

95

31* Цит. по: Сарамаго Ж. Перебои в смерти [2005] / пер. А. Богдановского. СПб.: Азбука, 2015. С. 221.

(обратно)

96

8. В качестве образцов искусства, воспринимаемого как красивое вне зависимости от культурной принадлежности зрителя, мы приводим здесь лубочные ткани племен мбути, изображенные на рис. 4.3 в книге Рона Иглаша (Eglash R. African Fractals: Modern Computing and Indigenous Design. New Brunswick, NJ: Rutgers University Press, 1999); анималистическую скульптуру инуитов, показанную на рис. 133 в книге Бернадетт Дрисколл (Driscoll B. Uumajut: Animal Imagery in Inuit Art. Winnipeg, MB: Winnipeg Art Gallery, 1985); а также наскальные рисунки в пещере Ласко и мозаики из Мескиты (мечети Кордовы) в Испании, позаимствованные со страниц «Истории искусств» Х. В. Янсона (Janson H. W. History of Art, 4^th ed. New York: Abrams, 1991. Рус. пер.: Янсон Х. В. Основы истории искусств [1986] / пер. М. Абушика, Э. Андреевой, И. Комаровой, И. Разумовской, С. Самостреловой, Е. Табанюхиной, М. Тарасова, В. Фатеева, А. Черноглазова. СПб.: АОЗТ ИКАР, 1996).

(обратно)

97

9. Возможно, это была книга: Hall D. Klee. Oxford: Phaidon, 1977.

(обратно)

98

10. Darwin C. On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. London: John Murray, 1859; Darwin C. The Descent of Man, and Selection in Relation to Sex. London: John Murray, 1871. На русском см., например, издания: Дарвин Ч. Происхождение видов [1859] / пер. К. А. Тимирязева. М.: Эксмо, 2016; Дарвин Ч. Происхождение человека и половой отбор [1871] / пер. И. М. Сеченова // Ч. Дарвин. Соч. в 2 т. М.: Терра, 2009.

(обратно)

99

11. Результаты исследования эстетического отбора Ричарда Прама блестяще изложены его книге «Эволюция красоты» (Prum R. The Evolution of Beauty: How Darwin’s Forgotten Theory of Mate Choice Shapes the Animal World – and Us. New York: Doubleday, 2017) и в его лекции на TEDxYale: https://www.youtube.com/watch?v=128-i8ulC7o

(обратно)

100

32* Альфред Уоллес (1823–1913) – британский натуралист, путешественник, географ, биолог и антрополог.

(обратно)

101

12. Fisher R. The Evolution of Sexual Preference // Eugenics Review. Vol. 7. 1915. P. 184–191.

(обратно)

102

13. Zahavi A. Mate Selection: A Selection for a Handicap // Journal of Theoretical Biology. Vol. 53. 1975. P. 205–214.

(обратно)

103

14. Kirkpatrick M. The Handicap Mechanism of Sexual Selection Does Not Work // American Naturalist. Vol. 127. 1986. P. 222–240; Grafen A. Sexual Selection Unhandicapped by the Fischer Process // Journal of Theoretical Biology. Vol. 144. 1990. P. 473–516.

(обратно)

104

15. Функция y = f(x) является линейной, если y и x изменяются пропорционально, и нелинейной, если y и x изменяются непропорционально. Например, y = 5(x) – линейная функция, поскольку при любом изменении значения x значение y будет меняться пропорционально (в данном случае оно будет увеличиваться в пять раз). Зато y = x² – нелинейная функция, потому что если мы умножим x на 2, то y умножится на 4, а если умножим x на 3, то y умножится на 9: изменение y непропорционально изменению x.

(обратно)

105

16. Цит. по: Prum R. The Evolution of Beauty: How Darwin’s Forgotten Theory of Mate Choice Shapes the Animal World – and Us. New York: Doubleday, 2017. P. 186, 188.

(обратно)

106

17. Понятие адаптивного ландшафта описано Сьюаллом Райтом в его статьях: Wright S. Evolution in Mendelian populations // Genetics. Vol. 1. 1932. P. 97–159 и Wright S. The Role of Mutation, Inbreeding, Crossbreeding, and Selection in Evolution // Proceedings of the Sixth International Congress of Genetics. Vol. 1. 1932. P. 356–366.

(обратно)

107

18. Кэтрин Джонсон стала героиней великолепного фильма «Скрытые фигуры» («Двадцатый Век Фокс», 2016).

(обратно)

108

19. Нумерация Гёделя описана в книгах: Нагель Э., Ньюмен Дж. Теорема Гёделя [1958] / пер. Ю. А. Гастева. М.: КРАСАНД, 2009; Хофштадтер Д. Р. Гёдель, Эшер, Бах. Эта бесконечная гирлянда [1979] / пер. М. А. Эскиной. Самара: Бахрах-М, 2001.

(обратно)

109

20. Рус. пер.: Саган К. Космос [1980]. СПб.: Амфора, 2005. С. 25–26.

(обратно)

110

21. Утверждение о том, что треугольник Серпинского – единственная фигура, которая не изменяется в результате применения трех правил треугольника Серпинского, имеет некоторую оговорку. Об этой оговорке «мелким шрифтом» рассказано в Приложении.

(обратно)

111

22. Множество Мандельброта описано и проиллюстрировано в главе 19 книги: Мандельброт Б. Фрактальная геометрия природы [1982] / пер. А. Р. Логунова. М.: Институт компьютерных исследований, 2002. Широкая публика впервые узнала о множестве Мандельброта из статьи Dewdney A. K. Computer Recreations: Exploring the Mandelbrot Set // Scientific American. Vol. 253. August 1985. P. 16–21, 24; название статьи вынесено в заглавие журнального выпуска. Об открытии множества Мандельброта рассказывается в главе 25 воспоминаний Бенуа Мандельброта: Mandelbrot B. The Fractalist: Memoir of a Scientific Maverick. New York: Random House, 2012.

(обратно)

112

23. Статья, которую мы с Дэйвом Пиком написали по результатам нашей работы с Генри Гурвицем: Hurwitz H., Frame M., Peak D. Scaling Symmetries in Nonlinear Dynamics: A View from Parameter Space // Physica D. Vol. 81. 1995. P. 23–31.

(обратно)

113

1. Существует некоторая путаница, когда разветвления тропинок в борхесовском «Саду расходящихся тропок» (см. упомянутый в первой главе сборник) сравнивают с многомировой интерпретацией квантовой механики Хью Эверетта (см.: Everett H. The Many-Worlds Interpretation of Quantum Mechanics / ed. B. DeWitt, N. Graham. Princeton, NJ: Princeton University Press, 1973). Как замечательно объяснил Шон Кэрролл в своей книге «Квантовые миры и возникновение пространства-времени» (Кэрролл Ш. Квантовые миры и возникновение пространства-времени [2021] / пер. О. Сивченко. СПб.: Питер, 2022), в результате макроскопического выбора Вселенная не разветвляется надвое: разветвление происходит лишь на уровне измерений квантовых состояний, если применять к Вселенной многомировую модель.

(обратно)

114

2. Удивительные книги Карло Ровелли о природе времени и реальности с точки зрения современной квантовой физики и теории относительности: Ровелли К. Нереальная реальность: Путешествие по квантовой петле [2014] / пер. А. Сергеева. СПб.: Питер, 2020; и Ровелли К. Срок времени [2014] / пер. Д. Баюка. М.: Corpus, 2020.

(обратно)

115

3. «Урок литературного творчества» – это третья глава книги Курта Воннегута «Человек без страны» (Воннегут К. Человек без страны, или Америка разБУШевалась [2005] / пер. Т. Рожковой. М.: АСТ, 2010).

(обратно)

116

33* Джон Макфи (род. 1931) – американский журналист, писатель, много лет ведет курс писательского мастерства в Принстонском университете.

(обратно)

117

4. Джон Макфи проводит параллели между географическими и повествовательными структурами в главе «Structure» книги: McPhee J. Draft No. 4: On the Writing Process. New York: Farrar, Strauss and Giroux, 2017.

(обратно)

118

5. Брайсон Б. Прогулка по лесам [1998] / пер. Е. С. Тортуновой. М.: Эксмо-Пресс, 2016.

(обратно)

119

6. Фильм Хэла Эшби «Будучи там» («Юнайтед Артистс», 1979) основан на романе Ежи Косински «Садовник».

(обратно)

120

7. Jamison L. The Empathy Exams. Minneapolis: Graywolf Press, 2014.

(обратно)

121

34* Хофштадтер Д. Р. Гёдель, Эшер, Бах. Эта бесконечная гирлянда [1979] / пер. М. А. Эскиной. Самара: Бахрах-М, 2001.

(обратно)

122

8. Когда вы смотрите на рисунок, вам может показаться, что большой разрыв на плоскости «игры Скраффи»-t никак не может соответствовать маленькому разрыву на заштрихованной плоскости. Однако помните, что траектория на заштрихованной плоскости не является проекцией траектории на плоскости «игры Скраффи»-t. Они обе являются проекциями траектории, находящейся в пространстве более высокой размерности.

(обратно)

123

1. О фрактальной структуре кладбища, описанного в романе «Книга имен» (Сарамаго Ж. Книга имен [1997] / пер. А. С. Богдановского М.: Эксмо, 2010), Сарамаго пишет в своих «Записках» от 31 марта (Saramago J. The Notebook. London: Verso, 2010).

(обратно)

124

2. Первой обстоятельной книгой, манифестом фрактальной геометрии стала работа Бенуа Мандельброта «Фрактальная геометрия природы» (Мандельброт Б. Фрактальная геометрия природы [1982] / пер. А. Р. Логунова. М.: Институт компьютерных исследований, 2002). С момента ее выхода появилось много других книг о фракталах. Книга для детей: Campbell S., Campbell R. Mysterious Patterns: Finding Fractals in Nature. Honesdale, PA: Boyds Mills, 2014; для широкого круга читателей: Falconer K. Fractals: A Very Short Introduction. Oxford: Oxford University Press, 2013; для преподавателей: Frame M., Mandelbrot B. Fractals, Graphics, and Mathematics Education. Washington, DC: Mathematical Association of America, 2002; для студентов: Falconer K. Fractal Geometry: Mathematical Foundations and Applications, 3^rd ed. Chichester: Wiley, 2014; Frame M., Urry A. Fractal Worlds: Grown, Built, and Imagined. New Haven, CT: Yale University Press, 2016; Peak D., Frame M. Chaos under Control: The Art and Science of Complexity. New York: Freeman, 1994; Peitgen H.-O., Jürgens H., Saupe D. Chaos and Fractals: New Frontiers in Science, 2^nd ed. New York: Springer, 2004; а также Pesin Y., Climenhaga V. Lectures on Fractal Geometry and Dynamical Systems. Providence, RI: American Mathematical Society, 2009; для аспирантов: Falconer K. Techniques of Fractal Geometry. Chichester: Wiley, 1997; и множество, возможно, сотни, сборников докладов.

(обратно)

125

3. О вычислении размерности мы немного расскажем в Приложении.

(обратно)

126

4. Некоторые подробности, касающиеся вычислений длины и площади треугольника Серпинского, а также соотношения между размерностью и размерами, представлены в Приложении.

(обратно)

127

5. Простая гипотеза о жизни в нецелочисленных измерениях представлена в разделе 6.7 книги «Фрактальные миры» (Frame M., Urry A. Fractal Worlds: Grown, Built, and Imagined. New Haven, CT: Yale University Press, 2016).

(обратно)

128

6. Макдональд Х. «Я» значит «ястреб» [2017] / пер. Н. Жутовской. М.: АСТ, 2017.

(обратно)

129

7. Роман Энн Панкейк «Какой бы странной ни была эта погода» (Pancake A. Strange as This Weather Has Been. Berkeley, CA: Counterpoint, 2007) рассказывает о том, как природные катаклизмы, причиной которых стала открытая добыча угля на юге Западной Виргинии, повлияли на членов одной семьи. Она описывает примерно те места, где я вырос, и те времена, когда я взрослел. Книга нескучная и не нравоучительная. В ней говорится о непростых и неидеальных людях, страдающих от последствий нелепой жадности и глупости.

(обратно)

130

1. Perl J. Causality: Models, Reasoning, and Inference, 2^nd ed. Cambridge: Cambridge University Press, 2009; Pearl J., Mackenzie D. The Book of Why: The New Science of Cause and Effect. New York: Basic Books, 2018.

(обратно)

131

2. Roger Ebert’s Journal, 14 January 2009, https://www.rogerebert.com/rogers-journal/i-feel-good-i-knew-that-iwould

(обратно)

132

3. Из посвящения в книге Перла «Каузальность».

(обратно)

133

35* Frame M., Urry A. Fractal Worlds: Grown, Built, and Imagined. New Haven, CT: Yale University Press, 2016.

(обратно)

134

1. Мы с Дэйвом Пиком написали «Хаос под контролем» (Frame M., Peak D. Chaos under Control: The Art and Science of Complexity. New York: Freeman, 1994) в качестве учебного пособия по фракталам и хаосу для студентов-гуманитариев Юнион-колледжа. Примерно двадцать лет спустя мы с Амелией Урри написали «Фрактальные миры» (Frame M., Urry A. Fractal Worlds: Grown, Built, and Imagined. New Haven, CT: Yale University Press, 2016) для соответствующего курса в Йельском университете. За годы, прошедшие между появлением этих двух книг, данная научная область значительно расширилась, как расширилось и мое понимание предмета. По иронии судьбы, «Фрактальные миры» увидели свет вскоре после того, как я покинул Йельский университет и вышел на пенсию, так что я не воспользовался этой книгой в качестве учебного пособия.

(обратно)

135

2. Джон Макфи – один из самых замечательных авторов литературы в жанре нон-фикшн. Говорят, он писатель, использующий один-единственный прием – глубоко заинтересовать читателя темой своей книги, какой бы эта тема ни была. А делает он это ловко. В книге «Черновик № 4» (McPhee J. Draft No. 4: On the Writing Process. New York: Farrar, Strauss and Giroux, 2017) Макфи описывает свой писательский процесс, добавляя в повествование немного геометрии.

(обратно)

136

3. Романы Лары Санторо рассказывают о скорби и утрате. Действие первого, «Милосердие» (Santoro L. Mercy. New York: Other Press, 2007), разворачивается в охваченной эпидемией СПИДа Африке; события второго романа, «Мальчик» (Santoro L. The Boy. New York: Little Brown, 2013), происходят на юго-западе США – и здесь показана более личная скорбь. Оба романа мощные, яркие и откровенные. Я с нетерпением жду выхода ее следующей книги.

(обратно)

137

4. Представьте мое удивление, когда я обнаружил, что стал героем пьесы Андреа Слоан Пинк «Фракталэнд» (Sloan Pink A. Fractaland / ed. W. W. Demastes // The Best American Short Plays, 2013–2014. Milwaukee: Applause Theatre & Cinema Books, 2015. P. 249–263). Она настолько точно изобразила Бенуа и меня, что я даже подумал, будто Андреа была моей студенткой; на самом деле мы не были знакомы, но между нами завязалась переписка по электронной почте, которая продолжается и сейчас. Из-за того что мы оба примерно одновременно потеряли родных, в письмах мы, естественно, обсуждали вопросы скорби.

(обратно)

138

5. Геометрическая модель юмора представлена Джоном Алленом Паулосом в книге «Математика и юмор» (Paulos J. A. Mathematics and Humor. Chicago: University of Chicago Press, 1980).

(обратно)

Флибуста

Геометрия скорби. Размышления о математике, об утрате близких и о жизни (fb2)

Майкл Фрейм Геометрия скорби. Размышления о математике, об утрате близких и о жизни

Пролог

* * *

* * *

1. Геометрия

* * *

* * *

* * *

* * *

2. Скорбь

* * *

3. Красота

4. Повествование

5. Фрактал

6. По ту сторону

Приложение: добавим математики

СКОЛЬКО КУБОВ ОГРАНИЧИВАЮТ ГИПЕРКУБ?

ПОЧЕМУ √2 – ИРРАЦИОНАЛЬНОЕ ЧИСЛО?

О ФРАКТАЛАХ МЕЛКИМ ШРИФТОМ

НЕМНОГО О ФРАКТАЛЬНОЙ РАЗМЕРНОСТИ

Благодарности

* * *

Примечания

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

Майкл Фрейм
Геометрия скорби. Размышления о математике, об утрате близких и о жизни