Implementation of the free energy methods in NAMD

The procedures implemented in NAMD are particularly adapted for performing free energy calculations that split the $\lambda$ reaction path into a number of non-physical, intermediate states, or ``windows''. Separate simulations can be started for each window. Alternatively, the TCL scripting ability of NAMD can be employed advantageously to perform the complete simulation in a single run. An example, making use of such a script, is supplied at the end of this section.

The following keywords can be used to run alchemical free energy calculations, whether FEP or TI.

• alch $<$ Is an alchemical transformation to be performed? $>$
  Acceptable Values: on or off
  Default Value: off
  Description: Turns on alchemical transformation methods in NAMD.

• alchType $<$ Which method is to be employed for the alchemical transformation? $>$
  Acceptable Values: fep or ti
  Default Value: ti
  Description: Turns on Hamiltonian scaling and ensemble averaging for alchemical FEP or TI.

• alchLambda $<$ Current value of the coupling parameter $>$
  Acceptable Values: positive decimal between 0.0 and 1.0
  Description: The coupling parameter value determining the progress of the perturbation for FEP or TI.

• alchLambda2 $<$ Forward projected value of the coupling parameter $>$
  Acceptable Values: positive decimal between 0.0 and 1.0
  Description: The lambda2 value corresponds to the coupling parameter to be used for sampling in the next window. The free energy difference between alchLambda2 and alchLambda is calculated. Through simulations at progressive values of alchLambda and alchLambda2 the total free energy difference may be determined.

• alchLambdaIDWS $<$ Backward value of the coupling parameter for Interleaved Double-Wide Sampling $>$
  Acceptable Values: decimal smaller than 1.0
  Description: Setting this parameter between 0 and 1 activates Interleaved Double-Wide Sampling (IDWS), whereby the target lambda value alternates between alchLambda2 and alchLambdaIDWS. The switch occurs every fullElectFrequency steps if defined, or nonbondedFrequency otherwise. Setting this parameter to a negative value (including between run statements) disables IDWS. When IDWS is active, the alchemy output file contains FepEnergy line headers for the forward energy differences, and FepE_Back for backward energy differences. FEP free energy estimates are based on forward data only. This file may be postprocessed with deinterleave_idws.py to produce separate files for the forward and backwards samples.

• alchEquilSteps $<$ Number of equilibration steps in a window, prior to data collection $>$
  Acceptable Values: positive integer less than numSteps or run
  Default Value: 0
  Description: In each window alchEquilSteps steps of equilibration can be performed before ensemble averaging is initiated. The output also contains the data gathered during equilibration and is meant for analysis of convergence properties of the alchemical free energy calculation.

• alchFile $<$ pdb file with perturbation flags $>$
  Acceptable Values: filename
  Default Value: coordinates
  Description: pdb file to be used for indicating the status of all atoms pertaining to the system, with respect to the alchemical transformation. If this parameter is not declared specifically, then the pdb file specified by coordinates is utilized for this information.

• alchCol $<$ Column in the alchFile that carries the perturbation flag $>$
  Acceptable Values: X, Y, Z, O or B
  Default Value: B
  Description: Column of the pdb file to use for retrieving the status of each atom, i.e. a flag that indicates which atom will be perturbed in the course of the alchemical transformation. A value of -1 in the specified column indicates that the atom will vanish as $\lambda$ moves from 0 to 1, whereas a value of 1 indicates that it will grow.

• alchOutFreq $<$ Frequency of free energy output in time-steps $>$
  Acceptable Values: positive integer
  Default Value: 5
  Description: Every alchOutFreq number of MD steps, the output file alchOutFile is updated by dumping energies that are used for ensemble averaging. This variable could be set to 1 to include all the configurations for ensemble averaging. Yet, it is recommended to update alchOutFile energies at longer intervals to avoid large files containing highly correlated data, unless a post-treatment, e.g. Bennett's acceptance ratio (BAR) [5] or simple overlap sampling (SOS) [58], is to be performed.

• alchOutFile $<$ Alchemical free energy output filename $>$
  Acceptable Values: filename
  Default Value: outfilename
  Description: An output file named alchOutFile, containing the FEP energies, or tiOutFile, containing the TI derivatives, dumped every alchOutFreq steps.

• alchVdwShiftCoeff $<$ Soft-core van der Waals radius-shifting coefficient $>$
  Acceptable Values: positive decimal
  Default Value: 5
  Description: This is a radius-shifting coefficient of $\lambda$ that is used to construct the modified vdW interactions during alchemical free energy calculations. Providing a positive value for alchVdWShiftCoeff ensures that the vdW potential is finite everywhere for small values of $\lambda$ , which significantly improves the accuracy and convergence of FEP and TI calculations, and also prevents overlapping particles from making the simulation unstable. During FEP and TI, assuming $\lambda = 0$ denotes an absence of interaction, the interatomic distances used in the Lennard-Jones potential are shifted according to [7,60]: $r^2 \rightarrow r^2 + {\tt alchVdWShiftCoeff} \times (1 - \lambda)$

• alchElecLambdaStart $<$ Value of $\lambda$ to introduce electrostatic interactions $>$
  Acceptable Values: positive decimal
  Default Value: 0.5
  Description: In order to avoid the so-called ``end-point catastrophes'', it is crucial to avoid situations where growing particles overlap with existing particles with an unbounded interaction potential, which would approach infinity as the interaction distance approaches zero [7,22]. One possible route for avoiding overlap of unbounded electrostatic potentials consists of allowing a bounded (soft-core) vdW potential, using a positive value of alchVdWShiftCoeff, to repel first all overlapping particles at low values of $\lambda$ . As $\lambda$ increases, once the particles are repelled, it becomes safe to turn on FEP or TI electrostatics.

  In the current implementation, the electrostatic interactions of an exnihilated, or appearing, particle are linearly coupled to the simulation over the $\lambda$ value range of alchElecLambdaStart - 1.0. At $\lambda$ values less than or equal to the user-defined value of alchElecLambdaStart, electrostatic interactions of the exnihilated particle are fully decoupled from the simulation. Coupling of electrostatic interactions then increases linearly for increasing values of $\lambda$ until $\lambda$ =1.0, at which point electrostatic interactions of the exnihilated particle are fully coupled to the simulation.

  For annihilated, or vanishing, particles the electrostatic interactions are linearly decoupled from the simulation over the $\lambda$ value range of 0 - (1.0 - alchElecLambdaStart). At $\lambda$ =0 electrostatic interactions are fully coupled to the simulation, and then linearly decreased with increasing $\lambda$ such that at $\lambda$ values greater than or equal to (1.0 - alchElecLambdaStart) electrostatic interactions are completely decoupled from the simulation. Two examples, shown in Figure 9, describe the relationship between the user-defined value of $\lambda$ and the coupling of electrostatic or vdW interactions to the simulation.

  Figure: Relationship of user-defined $\lambda$ to coupling of electrostatic or vdW interactions to a simulation, given specific values of alchElecLambdaStart or alchVdwLambdaEnd.

  

• alchVdwLambdaEnd $<$ Value of $\lambda$ to cancel van der Waals interactions $>$
  Acceptable Values: positive decimal
  Default Value: 1.0
  Description: If the alchElecLambdaStart option is used, it may also be desirable to separate the scaling of van der Waals and electrostatic interactions. alchVdwLambdaEnd sets the value of $\lambda$ above which all vdW interactions are fully enabled for exnihilated particles.

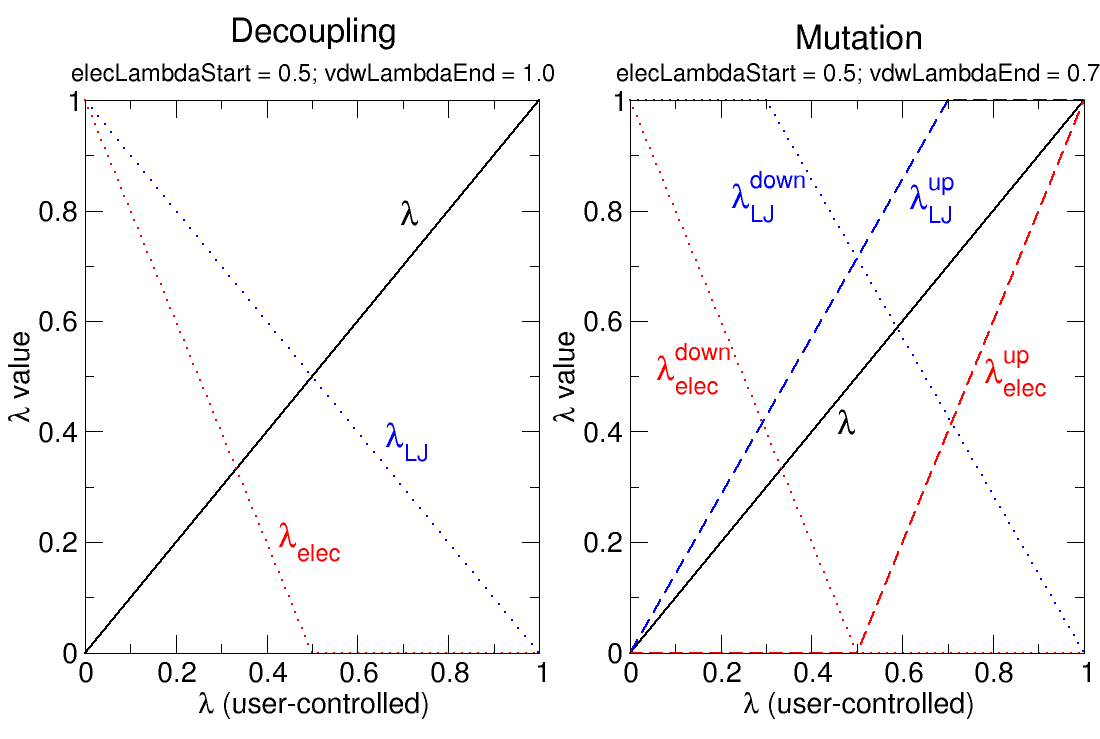  For an exnihilated particle, vdW interactions are fully decoupled at $\lambda$ =0. The coupling of vdW interactions to the simulation is then increased with increasing values of $\lambda$ such that at values of $\lambda$ greater than or equal to alchVdwLambdaEnd the vdW interactions of the exnihilated particle are fully coupled to the simulation.

  For an annihilated particle, vdW interactions are completely coupled to the simulation for $\lambda$ values between 0 and (1 - alchVdwLambdaEnd). Then, vdW interactions of the annihilated particle are linearly decoupled over the range of $\lambda$ values between (1 - alchVdwLambdaEnd) and 1.0. VdW interactions are only fully decoupled when $\lambda$ reaches 1.0.

  New as of version 2.12: The energy and virial terms added by LJcorrection on are now also controlled by the vdW $\lambda$ schedule. The average Lennard-Jones $A$ and $B$ coefficients are computed separately at both endpoints and then coupled linearly. In most practical situations the energy difference is extremely negligible, but this is more theoretically sound than the old behavior of averaging both endpoints together. However, the kinetic energy component of the virial does still count the endpoints together, as if annihilated alchemical atoms were an ideal gas. Again, this is likely quite negligible, nor is it clear that this should be treated specially.

• alchBondLambdaEnd $<$ Value of $\lambda$ to cancel bonded interactions $>$
  Acceptable Values: positive decimal
  Default Value: 0.0
  Description: New as of version 2.12 Bonded terms involving alchemical atoms may now also be scaled on a schedule similar to vdW interactions. Although this is more theoretically sound in many situations, this behavior is off by default.

• alchBondDecouple $<$ Enable scaling of bonded terms within alchemical groups $>$
  Acceptable Values: on or off
  Default Value: off
  Description: This is essentially a bonded term analogue of the alchDecouple keyword. Setting alchBondDecouple on, causes bonded terms between alchemical atoms in the same group to also be scaled. This means that alchemical atoms are annihilated into ideal gas atoms instead of ideal gas molecules. In this case it is recommended to use the approach of Axelsen and Li [3] by way of the extraBonds keyword. Using alchBondDecouple on is strictly necessary if it is desired to have the endpoint (potential) energies of a dual-topology PSF match those of a non-alchemical PSF.

• alchDecouple $<$ Disable scaling of nonbonded interactions within alchemical partitions $>$
  Acceptable Values: on or off
  Default Value: off
  Description: With alchDecouple set to on, only nonbonded interactions of perturbed, incoming and outgoing atoms with their environment are scaled, while interactions within the subset of perturbed atoms are preserved. On the contrary, if alchDecouple is set to off, interactions within the perturbed subset of atoms are also scaled and contribute to the cumulative free energy. In most calculations, intramolecular annihilation free energies are not particularly informative, and decoupling ought to be preferred. Under certain circumstances, it may, however, be desirable to scale intramolecular interactions, provided that the latter are appropriately accounted for in the thermodynamic cycle [22].