An Engineering Approach to Investigate Biological Visuo-Motor Control
Survey of the Project:
"An Engineering Approach to Investigate Biological Visuo-Motor Control"
- Introduction
- Biologically Plausible Models of Motor Control
- Visual Processing for Motor Control
- Robot Control with the "Neural Gas" Algorithm
- Comparing Models of the Visual Cortex
- The Development of the Primary Visual Cortex
- Morphogenesis of the Lateral Geniculate Nucleus
- Synchronous Neural Activity in the Visual Cortex
- On-Line Learning Processes
Introduction
This report presents a summary of research, funded by the Carver Charitable Trust, undertaken by members of the Theoretical Biophysics Group of the Beckman Institute at the University of Illinois at Urbana-Champaign under the direction of Professor Klaus Schulten. The work discussed covers the period from March 1993 to February 1994, i.e., the second and final period of funding provided by the Carver Charitable Trust. The research pursued in this period extends and develops upon the original aim of the project, namely, development of a unified model of visuo-motor control employing known biological principles. The primary aim of the research has been to develop neural architectures capable of effecting control of the robot system illustrated in the figure.
The approach adopted by the group remains as outlined in the report on the work covering the previous funding period submitted to the Carver Charitable Trust, namely, individual group members each pursue their own project, but collaborate closely on the many aspects which are common to the projects. The principal themes of the research, as presented in the previous report, include:
- visual processing
- postural control
- control of manipulation
- optimization of movement
- learning strategies
The notable feature of the work described in the present report is the increasing sophistication of the approaches employed to address the many unresolved issues surrounding visuo-motor control in biological systems.
Biologically Plausible Models of Motor Control
Introduction
To date, models of visuo-motor control in biological systems, have, to a large extent, been confined to systems capable of performing simple sensory-to-motor transformations. For example, in employing neural algorithms to control the SoftArm, the research effort of the group was devoted to developing networks that were capable of learning the transformations between the visual coordinates of the end effector of the robot and the motor commands necessary to position the end effector at a given point. In contrast, however, movement in biological systems is the result of information processing occurring concurrently in a hierarchy of motor centers within the nervous system. Furthermore, while visual information is of great importance to movement it does not constitute the sole source of input to the nervous system. Proprioceptive input, that is information derived from sensors which signal the internal states of limbs themselves, is of the utmost importance for accurate motor control. This fact is reflected in the considerable area of the cerebral cortex devoted to processing information of this type. We want to clarify the manner in which the various centers associated with motor control within the cerebral cortex contribute to motor control. Furthermore, we wish to elucidate the manner in which these motor centers can jointly program and coordinate movement. This work is undertaken by Ken Wallace, a post-doctoral researcher who joined the group in 1992, having completed graduate research at the University of Oxford.
Description
During visually guided movements, information related to the visual field will initiate the process of programming the required movement. However, proprioceptive input will also be required to indicate the correct context within which the movement should be performed. This is necessary because limbs have many more degrees of freedom than is strictly necessary to allow movement in space. This introduces a degree of redundancy to the problem in which different muscles can be employed in varying fashions to achieve the same results. Furthermore, the ability of individual muscles to contribute to movement is, in general, dependent upon the starting and end points of the movement. Accurate control of movement requires, therefore, that the central nervous system is capable of taking account of these factors when calculating the optimal pattern of muscle recruitment to achieve the desired movement. In other words, a degree of ``context sensitivity" must be introduced into the programming of particular movements.
In extending the techniques and neural architectures that have been developed during the period of funding provided by the Carver Charitable Trust, our attention has now focussed upon models that are capable of accounting for the processing occurring within several distinct areas of the cerebral cortex. This issue draws largely from the existing body of knowledge regarding how individual areas of the brain respond during movement. The parietal cortex, for example, is known to be intimately involved in the association of exteroceptive input, that is information regarding the external environment, and proprioceptive sensory input. As such, the parietal cortex is able to associate visual signals regarding target and limb position with afferent input provided by body sensors indicating the current position of the limb. On the other hand, several structures, including the parietal cortex, sensory cortex and motor cortex, have been implicated in formulating the correct context of a movement.
We have developed a model which takes account of some of the principal stages responsible for sensory to motor transformations found within the cerebral cortex. This model explicitly accounts for processing occurring within the visual and the parietal cortices. In addition, it includes a lumped model of the motor areas of the cerebral cortex, mid-brain and spinal segmental level of motor control as well as certain types of proprioceptive information regarding the internal state of the limb. The neural networks of this simulation learn through the random exploration of the workspace of the SoftArm, in a similar fashion to the way a child makes random movements during play. During this process the system learns maps of commands which are capable of positioning the SoftArm at particular locations within the workspace. The figure illustrates the development of one such motor map, used to control movement of the "wrist" of the SoftArm, at four points during learning. The top left frame illustrates the state of this map prior to any learning. Here the colored squares represent the states of the individual motor cells which constitute this map. The top right hand frame illustrates the organization that has evolved in this map, following a period of learning corresponding to 1000 time steps. As can be seen, the basic structure of the map has already become evident. The lower left and right frames illustrate the subsequent development of this map after another 1000 and 2000 time steps, respectively. Only after this learning phase is the system capable of performing coordinated movement.
To date, we have been successful in employing this model to control coarse positioning of the SoftArm: at present, the error in the absolute position attained by the movement is between 3 and 9cm. The learning observed using this model is, however, very characteristic of the early stages of skilled movement acquisition observed during the development of motor skills in primates: highly accurate movements are only possible once the ability to learn more approximate positioning skills has been acquired. In addition, it is important to separate the distinct issues of positioning the limb and manipulation of the hand. In primates these functions, although related, reflect the action of distinct areas of not only the motor cortex, but also the basal ganglia and the cerebellum.
To pursue this work we have recently turned our attention to the question of how we can model the next stage of the learning process, that is the acquisition of more skilled movements. In this respect we are currently investigating how context sensitivity may be introduced into the present simulations. One particularly interesting aspect of the work employs the mechanical characteristics of the SoftArm. The compliance of the arm can be adjusted such that movements which are programmed in a similar manner reach entirely different end points in the workspace, depending upon the values specified for the muscles of the SoftArm. Such a situation is very reminiscent of the situation found in primates where it has been postulated that joint stiffness, the reciprocal of joint compliance, is explicitly modulated to achieve the desired end point of a movement.
References
Visual Processing for Motor Control
Introduction
In addition to addressing questions relating to strictly motor control aspects of visuo-motor control, we have also been active in adopting more biologically plausible methods for extracting salient information from the visual fields provided by the two cameras associated with the SoftArm. This research is been undertaken by Micah Yairi, a Physics major at the University of Illinois under the direction of Ken Wallace.
Description
In the original investigations of visuo-motor control, extracting the location of the end effector of the SoftArm was achieved by attaching a light emitting diode to either side of the effector. This presented two very bright point light sources which were easily identifiable, and from which the position and orientation of the end effector could be determined. However, this approach bares little resemblance to the manner in which biological systems visually guide motion. To improve upon this we have adopted a simple, but effective, color differentiation scheme which involves restricting the visual workspace, and any objects within it, to two highly contrasting colors, in this case black and white. This has been achieved by ensuring that the entire apparatus -- robotic arm, control system, and table, as well as all the surrounding area visible to either camera -- is white. Objects of interest, such as the end effector of the SoftArm or a target object to be grasped, conversely, are made black. The monochrome images of the visual workspace provided by the two cameras associated with the system are then thresholded such that areas of the image that are sufficiently white are masked out by this process. The only remaining objects are those dark enough not to be removed during thresholding.
With objects of potential interest in the visual field identified and extraneous visual input abolished, the location of the end effector must be established. In theory this requires the capacity to differentiate between any number of objects that might remain within the visual space following thresholding. However, to simplify the problem we restrict attention to situations in which only two distinct objects, corresponding to the location of the end effector and a target object, are present. As the target object to be grasped is assumed to be static, that is, if the location of this object in the visual space does not vary, it is possible by comparing a series of steps and investigating which object did not move, to identify the target. The figure illustrates the visual scene presented to one of the visual processing networks. The state of the visual network corresponding to the right ``eye" has been superimposed upon the monochrome image provided by the camera. This image has been thresholded to identify the end effector, indicated by the black area bordered by green, and the target, a rubber rat (Basil), outlined in red. The yellow and blue circles indicate the centers of these objects in the visual field, and the purple and green circles indicate the particular nodes in the visual network that provide the most accurate representation of the location in the visual space of the two objects.
Although this scheme is relatively robust and has a greater than 90% rate of accurately extracting the location of the end effector, it will, on occasion, fail to identify the correct objects within the visual space. These failures occur for a variety of reasons: lighting levels can generate spurious objects, the end effector and target objects may coalesce resulting in only one object being identified after thresholding, and the target location can alter as a result of being hit by the end effector during learning. To overcome these problems, therefore, we are currently incorporating an additional stage in the visual processing system, namely recognition of an object by shape. This is accomplished through use of a self-organizing feature map network which learns both the area and eccentricity of the end effector in the visual space as a function of location within the workspace. On completion of the learning phase this network is able to provide an additional source of input to the system to aid in establishing unequivocally the location of the end effector.
Future development goals include implementing additional networks capable of identifying the target on the basis of area and eccentricity data, such that the rather rigorous color restrictions, currently imposed upon visual workspace, may be relaxed. In addition, we will incorporate some of the approaches to visual processing, outlined elsewhere in this report, into our present system to further improve the biological fidelity of the work at both the visual and motor levels. In conclusion, we have to date succeeded in developing a model which captures some of the salient features of the motor system found in primates in a biologically plausible fashion. Future work will concentrate on improving the accuracy of the approach, such that it will be comparable with the accuracy demonstrated by real biological motor systems and by engineering-based neural architectures.
Robot Control with the "Neural Gas" Algorithm
Introduction
Our SoftArm robot and its related systems are not only a valuable analogue to the workings of biological visuo-motor coordination systems, but also serve as a flexible testbed for developing adaptive algorithms applicable in the real world. The robot's hysteretic behavior makes it extremely difficult to control with the accuracy needed for any real-world application. On the other hand, its unique physical flexibility is a very desirable quality in many applications, such as various human-robot interaction scenarios. To overcome the unpredictable aspects of controlling this robot, we use a biologically inspired adaptive algorithm -- the "neural gas" -- to realize accurate control. This work is carried out by Stanislav Berkovich. He rejoined the Theoretical Biophysics Group in November 1993 as a graduate student in Computer Science, after spending two years at Sony CRL, Tokyo.
Description
The initial state of the system (left). The state
after the setup phase (right): the neurons have "moved" into the
area of the workspace.
Our effort builds upon the group's prior research into developing and applying self-organizing neural network algorithms to allow the SoftArm robot to accurately position its end effector and grasp objects. This work is a continuation of that of Kakali Sarkar as described in last year's progress report. In short, we are applying the "neural gas" algorithm to map points in the four-dimensional visual input space (two two-dimensional camera images of the workspace) into control signals for our SoftArm robot.
The project is currently being modified to use a faster and more sophisticated vision system that is under development by other members of the group. In addition, the system has been optimized to use an order of magnitude fewer neurons to achieve a positioning accuracy limited only by the resolution of the cameras. As before, the robot positions its end effector by using successive movements, relying on feedback from the cameras to achieve successive corrections, until the positioning error reaches a desired tolerance (at which point the robot grasps a target at the desired position, as described in the previous literature). Each correction modifies the state of the neurons representing the visuo-motor map in such a way that successive positioning cycles reach the desired error with fewer corrective movements. The system, thus, does not distinguish between a "learning phase" and an "operating phase" since it continually adjusts its state to satisfy the error constraint. In this way, it can position the robot accurately, even when the physical characteristics of the robot change. However, a "setup phase" (about 200 cycles) is required to organize the neurons from their initial random state into a working visuo-motor map.
The key mechanism in the "neural gas" algorithm is its ability to break up the visual input space into smaller regions that can be represented more easily by local maps. In addition, it facilitates a co-operative approach for adapting these local maps. In other words, each local map evolves by using information from many of its neighboring maps (a trait common to biological systems). The figureigure shows the initial adaptation of the "neural gas". The "positions" of the neurons -- the centers of each neuron's mapping region -- are superimposed on an image of the workspace. The robot end effector and the rubber rat (Basil) are colored and shown in black. The small black rectangles represent the positions of the neurons projected onto the camera image. Future research will concentrate upon employing the algorithm in situations where accuracy is of principal importance, either in the context of movements performed by biological systems or for technical applications.
References
Comparing Models of the Visual Cortex
Introduction
One goal of our research is to use cameras for robot control in a biologically inspired manner by integrating units similar to cortical visual and motor maps. Important for this goal is an understanding of the principles underlying the structure of visual maps. Many different models have been proposed during the past two decades. We undertook a critical evaluation of the most prominent and successful of the alternative approaches. Our goals were to exclude unsatisfactory approaches, reveal common principles underlying seemingly different models, and determine which quantities are sensible to measure in order to decide between hypotheses. This work has been carried out by Ed Erwin, a graduate student in Chemical Physics who joined the group four years ago, in collaboration with Klaus Obermayer, a past graduate student in our group and currently at the University of Bielefeld, Germany. Experimental data for the comparisons were available through a collaboration with Gary Blasdel of Harvard Medical School.
Description
Many cells in the mammalian primary visual cortex are selective to certain features in visual input. For example, they respond better to stimulation of one eye over the other, and usually respond more strongly to bars or gratings of a particular orientation. The figure shows the lateral spatial pattern of ocular dominance and orientation selectivity in the striate cortex of an adult macaque. Examples are shown of several elements of the lateral organization which have been termed (1) singularities, (2) linear zones, (3) saddle points, and (4) fractures. These and similar large, high-resolution pictures have led to a greatly improved characterization of striate cortical organization in the macaque.
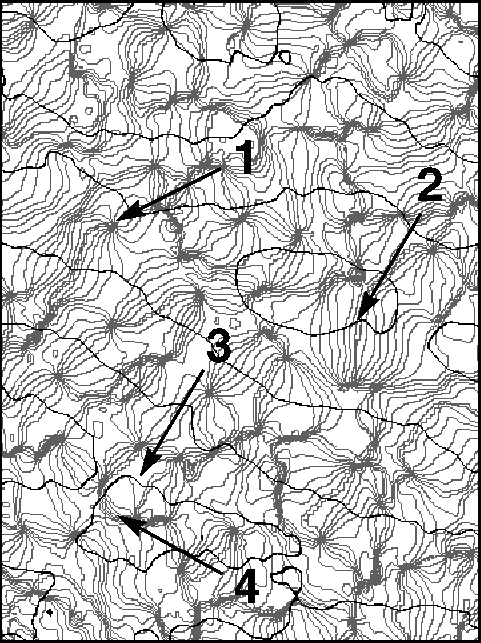The lateral spatial pattern of orientation
preference and ocular dominance in the striate cortex of an adult
macaque as revealed by optical imaging. The
figure shows a 4.1mm x 3.0 mm surface region located near the border between cortical areas 17
and 18 and close to the midline. Black contours separate bands of
opposite eye dominance. Light gray iso-orientation contour lines
separate regions responsive to orientations differing by
11.25 degrees. The medium gray contour represents the preferred
orientation 0 degree. Arrows indicate (1) singularities, (2) linear
zones, (3) saddle points, and (4) fractures.
Many models for the structure and formation of orientation and ocular dominance maps have been proposed. Although seemingly based on different assumptions, most produce maps which visually resemble the experimentally obtained maps. To sort through the conflicting claims, we extended and analysed the most prominent of the previously proposed models and compared their predictions with the experimental data.
For convenience we grouped the major models into classes and types based on similarities in goals or implementation. The two main classes are pattern models and developmental models. Pattern models attempt to provide a characterization of map patterns in schematic drawings or simple equations. They include both structural and spectral models. Developmental models give more attention to proposed mechanisms of pattern formation. Their pattern-generating equations are meant to correspond more closely to actual physiological processes. Developmental models include correlation-based learning, competitive Hebbian models, and several others.
This study revealed that several pattern models, as well as an entire class of developmental correlation-based learning models, are incompatible with experimental data, whereas competitive Hebbian models and several particular pattern models are in accordance with the experimental findings. Furthermore, we found that despite apparent differences, most models are based on similar principles and consequently make similar predictions.
The main results are as follows: Several pattern models and several developmental models generate maps which closely match the experimentally observed map patterns. Among the pattern models, the spectral models perform better than the previously proposed structural models, mainly because they account for global disorder and for the coexistence of linear zones and singularities. The filtered noise approach for orientation selectivity and for ocular dominance captures most of the important features of the individual maps, except for the high degree of feature selectivity which is observed in the macaque. Models by Swindale provide the currently best description of the patterns found in the macaque and can additionally account for the correlations between the orientation and ocular dominance maps. The close agreement, however, is reached at the expense of extreme simplification of the biological processes.
Among the developmental models, our analysis showed that the correlation-based learning models, which involve Hebbian learning but which include only linear intra-cortical interactions, perform well for ocular dominance. When applied to the formation of orientation maps, these models fail to predict the existence of linear zones and wrongly predict correlations between cells' orientation preferences and their spatial relationship in cortex. Correlation-based learning models have led to valuable insight into the role of Hebbian learning in receptive field development. However, to be applicable to cortical map formation, the nature of the lateral interaction must be changed.
Competitive Hebbian models --- which are based on non-linear lateral interactions --- lead to the currently best description of the observed patterns from a developmental model. These models attempt to describe the developmental process on a mesoscopic level, spatially as well as temporally, which has the advantage that the level of description matches the resolution of the experimental data. These models do not involve the microscopic concepts neuron, synapse and spike, which makes it somewhat more difficult to relate model predictions to experimental data.
Improvements on present models will require additional data on the spatial patterns. More stringent tests of the postulated mechanisms of activity-dependent neural development must rely on experiments which monitor the actual time-course of pattern formation, and which study pattern development under experimentally modified conditions (deprivation experiments). Mechanisms of visual cortex development should be fairly universal. Thus, any model of value should, additionally, be able to account for inter-species variations. Finally, one would like to have relatively simple models which make predictions about several aspects of cortical organization, such as receptive field location, color selectivity, receptive field sub-fields, and spatial phase. Correlations between maps of different features predicted by such models could be tested in suitably designed experiments.
References
The Development of the Primary Visual Cortex
Introduction
The study of the visual system is of great importance to both robotics and neuroscience. In the former case, much effort has gone into the development of engineering-type approaches towards the goal of functional machine vision systems. In the latter case, a great deal of experimental work has revealed the physical structure and functional organization of the visual systems of various species. We have sought to bridge the gap between these two fields by constructing a method of computer image processing which is based on current knowledge of how the human visual system works. Each field is enriched by the application of knowledge from the other. The field of robotics gains the use of methods employed by natural beings, whose capabilities far exceed robots of today. Neuroscience benefits from the powerful theoretical tools of artificial neural network techniques and image processing, resulting in a better understanding of the principles by which the brain can so effectively process information. In our work, we formulated a model of the development and functioning of the visual system, implemented the model in computer simulations to arrive at a mature, functioning system, and applied the system to images from the robot --camera system. This research is undertaken by Ted Hesselroth, a graduate student in the Physics Department. He joined our group three years ago.
Description
The model incorporates many details of the visual system which have been discovered experimentally. Included in the model are the functions of the retina, the lateral geniculate nucleus (LGN), and the primary visual cortex. The study of models of the primary visual cortex and the LGN have been major topics in our group.
The first area of visual processing is the retina of the eye, which not only collects light through the activity of the photoreceptors, but serves as a filter as well, through the action of center-surround cells. For so-called ON-center cells, light falling near the location of the cell causes excitation of the cell, while light that falls farther away inhibits cell activity. OFF-center cells have the reverse properties. When light of constant intensity illuminates the whole region around the cell, there is no cell activity, indicating that the input through the inhibitory and excitatory areas has been summed by the cell.
Information from the retina is transmitted through the optic nerve to the lateral geniculate nucleus. The LGN contains approximately the same number of neurons as the retina, and it is thought that the connections between the retina and the LGN are more or less one-to-one. For this reason neurons in the LGN also show center-surround receptive field properties.
The primary visual cortex, or area V1, contains neurons which respond to various features of the image. At this stage in the processing some analysis begins to take place. Feature selectivity is accomplished in a way similar to that in the center-surround cells previously described. The excitatory and inhibitory regions of V1 cells alternate and are elongated in a particular direction in retinal coordinates. In this way, the neurons respond most strongly to edges of a particular orientation. This yields a decomposition of the image according to its edges. This edge-detection is realized through feedforward connections from the LGN to V1. There exist also lateral connections between V1 neurons and reciprocal connections from V1 to the LGN. The latter are similar to the forward connections, but are inhibitory.
At the beginning of the simulation, all connection strengths are set to random values, and no coherent image processing can be achieved yet. By applying Hebbian learning to the connections, the neural network develops so as to produce V1 neurons which are orientationally selective as described above. It has been found experimentally that neurons in the V1 layer are organized according to their feature detecting properties. In the macaque monkey, the orientational selectivity of the neurons varies in a continuous way across the cortex, forming a ``feature map". Implementation of the model described produces organization in the V1 layer which closely resembles that found in experiments. The development of the orientational feature map obtained by the algorithm is shown in the figure.
We applied the model visual system to the robot-and-basil image. Shown in the figure is the image as seen via the edge detectors of the model. This illustration shows that the image is grasped by the feature-detecting properties developed in the primary visual cortex. This output is suitable for combining with motor cortex models to produce realistic models of visuo-motor control.
Morphogenesis of the Lateral Geniculate Nucleus
An example of a three-dimensional model of the macaque lateral geniculate nucleus (LGN). Each cell is represented by a
colored sphere, where the color codes for the type of the cell
receptive field. For the sake of clarity, only the 4 parvocellular
layers are depicted. The not shown 2 magnocelullar layers run parallel
to the 4 parvocellular ones and are not interrupted by the optic disk.
The location of the optic disk (not visible) determines where the
transition between patterns occurs.
Introduction
The lateral geniculate nucleus (LGN) is a layered structure found in all mammals. It is part of the visual pathway: it receives topographically organized input from both retinae and projects to the cerebral cortex. Virtually all visual information ascends via this route. It is generally believed that at the stage of the LGN an anatomical segregation of pathways conveying form and movement signals takes place. The massive feedback from the visual cortex to the LGN suggests another LGN function, namely, selective gain modulation of cell populations in the nucleus. Based on the extensive experimental results for the cell density, cell receptive fields, and spatial arrangement of the macaque LGN layers, it is now possible to develop a detailed model for the morphogenesis (development of structure) of the macaque LGN. This work is undertaken by Svilen Tzonev, a graduate student in the Physics Department who joined our group in 1992. We collaborate closely with Professor Malpeli of the Psychology Department of the University of Illinois on this project.
Description
In primates the LGN consists of several layers of neurons separated by intervening layers of axons and dendrites. The number of distinct layers varies in different parts of the LGN. In particular, in the posterior-anterior direction (going from rear to front) the macaque LGN has regions with 6, 4, and 2 layers. The cells comprising these layers are of different types (so-called magnocellular and parvocellular cells), have different input (from ipsilateral and contralateral eyes), and have different receptive field organizations (ON and OFF types of cells, see also elsewhere in this report). Each layer maps an entire hemifield of the visual space.
It should be emphasized that the overwhelming number of studies in which neural tissue properties and developmental rules have been modeled, considered only the synaptic relationships and functional properties of the neurons. In this project we attempt to model the specific brain morphology, i.e., to explain the observed topologically complex laminar structure in three dimensions consisting of 2, 4, or 6 layers depending on the part of the LGN. The transition between the 6- and 4-layer regions occurs at the position of the optic disk (the blind spot caused by the exit of the optic nerve from the eye). With our model we want to address the issue of the role of the optic disk in this transition.
To date we have established a mathematical framework for the morphogenesis of the LGN. In this general framework, emerging receptive fields of the LGN neurons are described by a two-component vector. Each component of this vector codes for one of the cell receptive field properties: eye specificity and polarity (ON/OFF) type. Simple rules, which can be written as effective interactions between retinal terminals, govern the emergence of specific neuronal receptive fields. These rules account for the formation of a strict retinotopic map, i.e., such that neighboring parts of the retina are mapped onto neighboring parts of the LGN. As has been observed in experiments, the receptive fields of LGN neurons develop gradually, starting from one part of the nucleus. A propagating wave of development of cell receptive fields then sweeps along the main axis of the LGN. Initially, one pattern (a 6-layer one) is the most stable state of the system and, consequently, it evolves to this pattern. By means of the described local interactions this pattern has a tendency to extend throughout the whole body of the LGN. However, because of changes in the effective interaction distances between retinal terminals, at some point a 4-layer pattern becomes the preferred stable state of the system. This occurs when the ratio between the layer thickness to the effective interaction distance reaches a critical value, which has been calculated analytically. Numerical experiments confirm the value of this critical ratio.
In an artificial model, restricted to one-dimensional retinae and a two-dimensional LGN, our simulations show that the transition between the two stable patterns does indeed coincide with the location of the optic disk. The optic disk, being a perturbation, however small, causes the system to switch to its most stable state: the 4-layer pattern. The two-dimensional situation is distinctly different in a topological sense from the three-dimensional one. In two dimensions the optic disk interrupts three of the six layers completely. In three dimensions, on the other hand, the essentially one-dimensional optic disc extends its influence on a two-dimensional layer and thus its effect is significantly smaller. We are currently running computer simulations of a three-dimensional system consisting of tens of thousands of neurons. The figure illustrates a typical simulation result of the modeling in three dimensions. We are still seeking to determine the necessary conditions under which the effect of the small perturbation will lead to the transition of the 6-layer to the 4-layer pattern. The way the retinotopy constraint (the fact that neighboring parts of the retina are mapped to neighboring parts in the LGN) is included in our model appears to play a crucial role in this developmental process and requires further attention.
References
Synchronous Neural Activity in the Visual Cortex
Introduction
Advances in information technologies have often been inspired by studies of cognitive processes in the brain. In order to obtain optimal algorithms for the processing of visual information, we want to achieve an understanding of the basic principles guiding biological visual processing. Von der Malsburg had earlier suggested that achieving firing correlation might allow the brain to link stimuli from the same visual object. Recently, experiments by Singer and others have revealed stimulus-dependent firing correlation between neurons of the visual cortex. Our aim was, thus, to understand the role of firing correlations in the visual cortex. This research has been conducted by Christian Kurrer, a graduate student in the Physics Department, who has been a member in our group for five years and has recently finished his dissertation research.
Description
This research started with simulations of large arrays of coupled neurons in order to investigate under which conditions synchronous firing activity is obtained. Our results showed that the occurrence of firing synchrony can be triggered by changes in the excitability of the neurons in the visual cortex. Investigations of this transition from asynchronous to synchronous firing showed that the onset of firing synchrony is always accompanied by a marked increase of the firing frequency. Therefore, we have proposed that achieving firing synchrony between neurons processing the same object might be a mechanism to increase the contrast between the object and its background. The notion that excitable neurons can synchronize their firing activity rapidly is important for understanding its role in visual processing, especially in such tasks as visual tracking. Visual tracking requires fast responses to constantly changing visual inputs.
The figure shows a typical simulation of neuronal firing activity. The three lower traces show the trans-membrane voltages of three different biological neurons, modeled by the Bonhoeffer-van der Pol (BvP) model. The neurons initially fire at a moderate frequency. At about one third through the simulation, the excitability of the neurons is increased. The neurons thereupon start to fire synchronously. The uppermost trace shows a measure for the firing correlation among the neurons. It shows that the neurons achieve almost maximal synchrony within two firing periods. At about two thirds through the simulation, the excitability is lowered back to its original value. The neurons rapidly loose their firing correlation. During the period of higher excitability, the neurons also fire at a higher frequency.
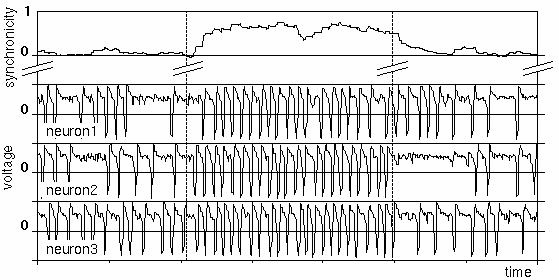Voltage traces of three interacting neurons (lower three curves). In the middle section, the excitability of the neurons has been increased, leading to firing synchronicity (top curve).
We have recently generalized these results by studying a more abstract model of neuronal dynamics which yielded the same effects. We were thus able to establish that the effects observed in simulations of BvP neurons are due to the fact that a BvP neuron behaves as an excitable system. This general result implies that firing correlation does not depend on the specific characteristics of neurons in the visual cortex and, therefore, plays a role in a variety of related recognition and response tasks. As an example, the recognition phase in the olfactory cortex is also characterized by oscillatory firing activity. Furthermore, this result also allows us to simulate the activity of biological neurons with much simpler excitable dynamical systems, such as active rotators. The use of these simplified neuron models will lead to a considerable computational speedup. This will allow one to use the concept of synchronous firing activity for biologically realistic, real-time processing of visual information, such as is required for visuo-motor control tasks.
References
On-Line Learning Processes
Introduction
Neural networks, like humans, learn from examples. In supervised learning, training examples consist of input-output pairs, e.g., inputs are the visual images of the target and of the robot arm, and outputs are the required controls in the form of pressure values for the robot actuators. A well-known example of unsupervised learning is the self-organization of feature maps as discussed elsewhere in this report. Practical applications of both supervised and unsupervised learning are based on sequential presentation of training patterns. A learning step takes place at each presentation of a single training example (so-called "on-line learning") or on account of a whole set of training patterns. From a biological point of view, learning from sets of training patterns is implausible. Therefore, we investigate the usefulness and advantages of on-line learning. This research is conducted by Tom Heskes, a post-doctoral researcher who joined our group in August 1993, coming from the University of Nijmegen.
Description
Learning after each presentation leads to some kind of randomness in the learning process. We showed that this stochasticity can help to prevent the network from getting stuck in suboptimal configurations, so-called "local minima" of the energy function that the learning rule tries to minimize. An example of such an energy function is the average squared distance between the robot's end effector and the target. A well-known technique to find the best possible configuration, the global minimum of the energy function, is simulated annealing. The randomness resulting from on-line learning has a similar effect, but in general, will lead to even better performance.
Through learning, neural networks build an internal representation of their environment. This representation is coded in the network's weights or synapses. To speed up learning, one often adds a so-called momentum term to the learning rule. With such a momentum term, the weight changes do not only depend on the current training example, but also on previous weight changes. Incorporation of the momentum term accelerates learning in regions where the energy function is relatively flat. We proved that, whereas the momentum term does help in speeding up learning from sets of examples, it has no effect whatsoever on learning from a sequence of single examples.
Supervised learning can be viewed as a process where a "teacher" (generating the desired network outputs given a particular input) tells the "student" (the neural network) what to do. Previous work on learning processes in neural networks has focussed on perfect conditions, that is, completely reliable "teachers". However, in practical applications, the assumption that teachers are completely reliable no longer holds. Noise in the learning process may be due to inaccuracy of the input data, output data, or to the noisy processing of the network weights. Studying a simple learning problem, we showed that different types of noise lead to different effects, e.g., output noise tends to be more destructive than input or processing noise. Furthermore, we suggested with an algorithm to improve the learning performance in these "noisy environments". The algorithm is "self-tuning", i.e., it uses information in the learning characteristics to optimize its performance. This makes the algorithm fairly insensitive to the type and magnitude of the noise. Further studies should aim at application of the algorithm to real-world problems.
