Principles addressed:

Big Idea IV. Algorithms: Algorithms are used to develop and express solutions to computational problems.
Key Concept A. An algorithm is a precise sequence of instructions for a process that can be executed by a computer.
Learning Objective 15: The student can develop an algorithm. [P2]
15a. Selection of appropriate techniques—such as sequencing, selection, iteration, and recursion—to develop an algorithm.
15b. Selection of appropriate combinations of algorithms to make new algorithms.
15c. Creation of an algorithm to solve a problem.
15d. Creation of an algorithm with a practical, personal, or societal intent.

>Learning Objective 16: The student can express an algorithm in a language. [P5]
-- 16a. Use of natural language, pseudo-code, or a visual or textual programming language to express an algorithm.
-- 16b. Explanation of how an algorithm is represented in natural language, pseudo-code, or a visual or textual programming language.
-- 16c. Explanation of how the language used to express an algorithm can affect characteristics such as clarity or readability.
-- 16d. Summary of the purpose of an algorithm.

CPSC 110-08: Computing with Mobile Phones

Algorithms

Introduction

In this lecture we will talk about algorithms. We'll look at many different examples. We'll learn about the types of components (steps) that make up algorithms, including sequence, selection, and repetition, and we'll learn how to develop and express some simple algorithms.

In computer science or mathematics an algorithm is a step-by-step method for performing a calculation. Each step in the algorithm must be unambiguous and doable. And there should be a finite number of steps.

We mean calculation in the broad sense that anything a computer does is a calculation. For example, changing the background color of a button when the user clicks on it is a calculation.

An algorithm is similar to recipe directions. But for algorithms we want to run on a computer the steps in a recipe are sometimes ambiguous.

5. Slowly blend in the flour mixture and mix until just combined. Do not overbeat.

An algorithm is similar to hair washing instructions. But some of its steps are ambiguous

Repeat application and rinse if hair is oily, or has excessive build-up.

Algorithms to Compute Sums

• Compute the sum of three numbers by hand, 5, 10, and 13.

  Write the word 'sum' on the board and put a 0 underneath it.
  Add 5 to the number written under 'sum' and put the result under 'sum'.
  Add 10 to the number written under 'sum' and put the result under 'sum'.
  Add 13 to the number written under 'sum' and put the result under 'sum'.
  The number written under 'sum' is the sum of 5, 10, and 13.
  

  In this example, the word 'sum' is like a variable. If we were writing this algorithm for App Inventor it might look like this, where Sum is a global variable.

  Set Sum to 0.
  Set Sum to Sum + 5
  Set Sum to Sum + 10
  Set Sum to Sum + 15
  

  Here's an App Inventor Procedure that implements this algorithm:

  Of course this algorithm is somewhat artificial. It doesn't really need 4 steps because it can be expressed more simply as:

  Questions:

  • Is there any reason to prefer one algorithm over the other?
  • Are both algorithms correct?
  • Is one more efficient than the other?
  • Is one more more clearly expressed than the other?
  • Is one easier to generalize than the other?

  Adding Three Numbers in a List

  Suppose we represent a list of numbers by using parentheses: (5 10 13). Here's an algorithm for calculating the sum of this list of 3 numbers.

  Set Sum to 0.
  Set Sum to Sum + the first number in the list.
  Set Sum to Sum + the second number in the list.
  Set Sum to Sum + the third number in the list.
  

  When we say the first number of the list we are indexing the list. This is a common step in computer algorithms.

  Here's an App Inventor Procedure that implements this algorithm. Note that the select list item block takes an argument for the list's index:

  Abstraction: Note how the argument slots in the select list item block generalize the operation of selecting an item from a list.

  Adding Just the Two-Digit Numbers in the List

  Suppose we wanted to add just the two-digit numbers in our list of three numbers. We could use this algorithm:

  Set Sum to 0.
  If the first number in the list >= 10
     Set Sum to Sum + the first number in the list.
  If the second number in the list >= 10
     Set Sum to Sum + the second number in the list.
  If the third number in the list >= 10
     Set Sum to Sum + the third number in the list.
  

  Or we could use this algorithm that uses a second global variable, called Number

  Set Sum to 0.
  Set Number to the first number in the list.
  If Number >= 10
     Set Sum to Sum + Number.
  Set Number to the second number in the list.
  If Number >= 10
     Set Sum to Sum + Number.
  Set Number to the third number in the list.
  If Number >= 10
     Set Sum to Sum + Number.
  

  Here's two App Inventor way to express these two algorithms:

  Questions:

  • Is there any reason to prefer one algorithm over the other?
  • Are both algorithms correct?
  • Is one more efficient than the other?
  • Is one more more clearly expressed than the other?
  • Is one easier to generalize than the other?

  Adding N Numbers in a List

  Suppose your list could have a variable number of numbers in it. Here's an algorithm for that.

  Set Sum to 0.
  Set Index to 1.
  While Index <= the length of the list
     Set Sum to Sum + the list item at Index
     Set Index to Index + 1
  

  Here's how we would do this in App Inventor

  Summary Observations

  • The basic unit of an algorithm is a statement.

    Statement Type	Example
    Assignment:	Set Sum to 0
    Assignment:	Set Sum to Sum + 10
    If/Then:	If Number > 10 then-do Set Sum to Sum + 10
    Loop:	While Index <= Length of List do: Set Index to Index + 1
    Procedure call:	Call SomeProcedure

  • Algorithms can be composed out of combinations of
    three basic control structures: sequence, selection (if/then), repetition or looping (while):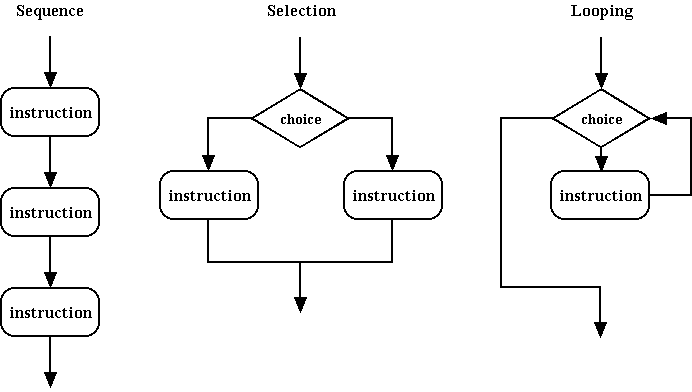
    

    Sequence	Selection	Repetition
    Set Sum to 0. Set Sum to Sum + 5 Set Sum to Sum + 10 Set Sum to Sum + 15	Set Sum to 0. If the first number in the list >= 10 Set Sum to Sum + the first number in the list. If the second number in the list >= 10 Set Sum to Sum + the second number in the list. If the third number in the list >= 10 Set Sum to Sum + the third number in the list.	Set Sum to 0. Set Index to 1. While Index <= the length of the list Set Sum to Sum + the list item at Index Set Index to Index + 1

  • Algorithms can be expressed in different languages

    Pseudocode	App Inventor	Java	Flowchart
    Set Sum to 0. Set Index to 1. While Index <= the length of the list Set Sum to Sum + the list item at Index Set Index to Index + 1		int sum = 0; int index = 0; while index < list.length { sum += list[index]; index += 1; }

  In-class Exercises

  1. Write a Pseudocode algorithm to sum all the single digit numbers in MyList storing the result in Sum.
  2. Test your algorithm by tracing it step-by-step on the list (14 5 3 21)
  3. Write an App Inventor version of this algorithm.
  4. Test your App Inventor algorithm by right clicking on blocks and using Watch and Do it.

  Homework Exercises (Due Friday)

  1. • Write a Pseudocode algorithm to compute whether or not a number is odd, storing the result, true or false, in a global variable.
     • Using your isOdd algorithm as a part, write a Pseudocode algorithm to sum all the odd numbers in MyList storing the result in Sum.
     • Test your algorithm by tracing it step-by-step on the list (14 5 3 21 5 6)
     • Write an App Inventor version of this algorithm.
     • Test your App Inventor algorithm by right clicking on blocks and using Watch and Do it.