 music |
 | OSdata.com |
Boolean logic
summary
This subchapter looks at Boolean logic.
free computer programming text book projecttable of contents
|
 music |
 | OSdata.com |
This subchapter looks at Boolean logic.
free computer programming text book projecttable of contents
|
This subchapter looks at Boolean logic.
Boolean algebra is named for George Boole, who introduced the ideas in the 1854 work “An Investigation of the Law of Thought”. Claude Shannon showed the application of Boolean algebra to switching circuits in the 1938 work “Symbolic Analysis of Relay and Switching Circuits”.
Major applications of Boolean algebra include:
Boolean algebra is a pure mathematical system that deals with perfect abstracts.
Real world logic circuits are physically imperfect implementations of Boolean algebra. Electrical problems (such as noise, interference, and heat) can cause failure. Delays in signals reaching certain locations (such as slew rate and propogation delay) can slow down cmputers and logic circuits and can produce nightmarish problems for computer and circuit designers. As processors and logic circuits shrink in size, quantum effects can even start to interfere with correct operation.
Boolean algebra is binary.
Objects can be one of two values: 1 or 0; true or false; high or low; positive or negative; closed or open; or any other pair of binary values.
The basic Boolean operations are AND, OR, and NOT.
The following chart shows the major interpretations of Boolean algebra:
| Boolean Algebra |
Truth Calculus | Switching Algebra | Logic Circuit | Set Theory Algebra of Classes |
||
| · multiplication |
AND | series circuit | intersection | |||
| + addition |
OR | parallel circuit | union | |||
| 0 | F | FALSE | open circuit | S(Z) | null set | |
| 1 | T | TRUE | short circuit | S(U) | universal set | |
| _ A |
¬A | NOT A | normally closed switch | C(S) | complemented set | |
AND requires both objects to be true for the result to be true. The AND works like a pair of switches in series. Both switches must be closed for current to flow.
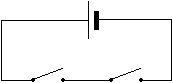
AND is conisdered to be Boolean multiplication and is represented by the middle dot symbol: · (such as A·B). As in ordinary algebra, AND (Boolean multiplication) can be written by dropping the middle dot (such as AB). There is no Boolean division operation.
The truth table for AND is as follows:
| A | B | result |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
The AND gate in logic circuits looks like:
![]()
The AND operation (Boolean multiplication) has the same results as ordinary arithmetic multiplication..
The AND operation has a result of 0 when any of its input variables is 0.
The AND operation has a result of 1 only when both of its input variables are 1.
OR (or inclusive or) requires either object to be true for the result to be true. The OR works like a pair of switches in parallel. Current will flow if either or both switches are closed.

OR is conisdered to be Boolean addition and is represented by the plus symbol: + (such as (A+B). There is no Boolean subtraction operation.
The truth table for OR is as follows:
| A | B | result |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
The OR gate in logic circuits looks like:
![]()
The OR operation has a result of 1 when any of its input variables is 1.
The OR operation has a result of 0 only when both of its input variables are 0.
In OR (Boolean addition) 1 + 1 = 1. Similarly, 1 + 1 + 1 = 1.
NOT (also called negation or complement) simply reverses the value of an object, changing true into false and changing false into true.
The truth table for NOT is as follows:
| A | result |
|---|---|
| 0 | 1 |
| 1 | 0 |
The NOT gate (or inverter) in logic circuits looks like:
![]()
As in ordinary algebra, in mixed expressions, all ANDs (Boolean multiplication) are performed before ORs (Boolean addition). For example, A+B·C is evaluated by ANDing B with C and then ORing A with the result of the first operation (BC).
Parenthesis can be used to change the ordinary order of evaluation. For example, (A+B)·C is evaluated by ORing A with B and then ANDing C with the result of the first operation (A+B). Parenthesis can be used for clarity.
Negation of a single variable or object is done before using the result in an expression. Negation of an entire expression is done after the expression is evaluated.
XOR (or exclusive or) is similar to the normal English meaning of the word “or” — a choice between two items, but not both or none. XOR is less commonly written EOR. The symbol for the XOR operation is ![]() .
.
The truth table for XOR (exclusive OR) is as follows:
| A | B | result |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
The XOR gate in logic circuits looks like:
![]()
XOR is not considered to be a basic Boolean operation, but is widely used in logic expressions. XOR is the same as ( (A) · (¬B) ) + ( (¬A) · (B ) ), extra parenthesis added for clarity.
NAND is the combination of a NOT and an AND. NAND produces the oppposite of an AND.
The truth table for NAND (Not AND) is as follows:
| A | B | result |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
The NAND gate in logic circuits looks like:
![]()
NOR is the combination of a NOT and an OR. NOR produces the opposite of OR.
The truth table for NOR (Not OR) is as follows:
| A | B | result |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
The NOR gate in logic circuits looks like:
![]()
XNOR (or NXOR) is the combination of a NOT and a XOR. XNOR produces the opposite of XOR.
The truth table for XNOR (Not eXclusive OR) is as follows:
| A | B | result |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
The XNOR gate in logic circuits looks like:
![]()
Coding example: I am making heavily documented and explained open source code for a method to play music for free — almost any song, no subscription fees, no download costs, no advertisements, all completely legal. This is done by building a front-end to YouTube (which checks the copyright permissions for you).
View music player in action: www.musicinpublic.com/.
Create your own copy from the original source code/ (presented for learning programming).
return to table of contents
free downloadable college text book
Because I no longer have the computer and software to make PDFs, the book is available as an HTML file, which you can convert into a PDF.
| previous page | next page |
| Tweets by @osdata |
free computer programming text book projectBuilding a free downloadable text book on computer programming for university, college, community college, and high school classes in computer programming. If you like the idea of this project, Supporting the entire project: If you have a business or organization that can support the entire cost of this project, please contact Pr Ntr Kmt (my church) free downloadable college text book on computer programming. |
This web site handcrafted on Macintosh ![]() computers using Tom Bender’s Tex-Edit Plus
computers using Tom Bender’s Tex-Edit Plus ![]() and served using FreeBSD
and served using FreeBSD ![]() .
.
†UNIX used as a generic term unless specifically used as a trademark (such as in the phrase “UNIX certified”). UNIX is a registered trademark in the United States and other countries, licensed exclusively through X/Open Company Ltd.
Names and logos of various OSs are trademarks of their respective owners.
Copyright © 2010 Milo
Created: November 1, 2010
Last Updated: November 5, 2010
return to table of contents
free downloadable college text book
| previous page | next page |