Página sobre Pseudo 3d de Lou

Traducción: Luis Peña

Actualización previa:

Una explicación de las matemáticas para la proyección en 3d (debajo de Las Bases de la Carretera) y análisis del Enduro de Activision (debajo de Casos de Análisis)!
Gracias a todos por los mails! Sigan así :) Lo siento, no puedo responder preguntas acerca de cuándo subiré código fuente, pero estoy siempre feliz de responder lo que sea acerca de estos motores!
Material oficial del motor gráfico de Road Rash y una explicación más detallada de las curvas y ecuación de curva generalizada

Es esta información imprecisa? Estoy lejos? No duden en escribirme a louis.gorenfeld en gmail punto com!

Tabla de contenidos

Por qué Pseudo 3d?
Ahora que los sistemas son capaces de producir gráficos con un montón de polígonos al vuelo..¿por qué quieres hacer una carretera a la vieja escuela? ¿No son los polígonos exactamente lo mismo, sólo que mejor? Bueno, no. Es verdad que los polígonos llevan a una menor distorsión,pero es la distorsión en estos viejos motores lo que les da ese aspecto surrealista y de velocidad exorbitante que se puede hallar en varios de los juegos de la era pre-polígonos. Piensa como si la vista estuviese controlada por una cámara. Al doblar una curva en uno de estos juegos, la cámara parece mirar alrededor de la curva. Luego, al enderezarse la carretera, la cámara también lo hace. Al tomar una curva ciega, la cámara parece mirar hacia abajo. Y, puesto que estos juegos no utilizan un formato de pista tradicional con relaciones espaciales perfectas, es posible crear sin esfuerzo pistas suficientemente grandes para que el jugador pueda ir a velocidades ridículas - sin preocuparse por un objeto que aparece en la pista más rápidamente de lo que el jugador puede posiblemente reaccionar ya que la realidad del juego puede adaptarse fácilmente al estilo de juego.

Pero también tienen muchos inconvenientes. La profundidad de las físicas de los juegos de simulación tiende a perderse. Estos motores no son adecuados para todos los propósitos. Sin embargo, son fáciles y rápidos de implementar, ejecutar, y son generalmente muy divertidos a la hora de jugar!

Vale la pena señalar que no todos los juegos de carreras antiguos usaron estas técnicas. De hecho, el método que se muestra aquí es sólo una forma posible de hacer una carretera pseudo 3d. Algunos utilizan sprites proyectados y escalados, otros parecen implicar diferentes grados de proyección real para el camino. Cómo tú mezclas las matemáticas con el "engaño" depende de ti. Espero que se diviertan tanto explorando este efecto especial como yo lo hice.

Cúanta matemática necesito?
Si tú...
...tienes conocimientos en trigonometría, eso es casi toda la matemática que necesitarás para este tutorial
...sólo tienes conocimientos en álgebra y geometría, saltéate la explicación del campo de visión
...quieres evitar las matemáticas todo lo posible, lee: La Carretera más Simple, Dirección y Curvas, Sprites y Datos, y Colinas

Esta es una técnica bastante flexible, y que realmente puedes lograr con tan sólo sumar! Con matemática más avanzada,puede ser mejor, pero solamente con la aritmética, puedes alcanzar el nivel de detalle visto en juegos como Pole Position o el primer OutRun.

Cuántos conocimientos de programación necesito?
Ayuda bastante entender los gráficos rasterizados: Saber qué es una scanline, y que cada línea está hecha de una fila de pixeles. Los ejemplos de programación están escritos en pseudocódigo, así que no necesitas tener experiencia en algún lenguaje para entenderlos.

Listo? Comencemos!

Efectos rasterizados - Un pantallazo
Una carretera en pseudo 3d es sólo una variación de una clase más general de efectos llamada efectos rasterizados (pixelados). Uno de los ejemplos mayormente conocidos de este efecto está en Street Fighter II: A medida que los luchadores se mueven izquierda y derecha, el suelo de desplaza en perspectiva. Esto no es realmente 3d.El suelo es almacenado como una captura en una perspectiva extremadamente ancha. Cuando la vista de desplaza, las líneas de la pantalla que se supone deben estár más lejos se mueven más lento que las líneas más cercanas. Esto quiere decir que cada línea de la pantalla se desplaza independientemente de las otras. Debajo se muestra el resultado final y cómo está almacenado en memoria el gráfico del suelo.

Introducción a las carreteras rasterizadas
Solíamos pensar (hasta ahora, claro ;D) en efectos 3d en términos de polígonos cuyos vértices están suspendidos en un espacio tridimensional. Los sistemas más viejos, sin embargo,no eran lo suficientemente poderosos como para realizar una gran cantidad de cálculos 3d. Muchos efectos antiguos,en general, caen dentro de la categoría de efectos rasterizados. Éstos son efectos especiales logrados cambiando alguna variables por línea. Más comúnmente, esto significa cambiar el color o la paleta por línea, o desplazarse por línea. Esto se ajusta bien al hardware de gráficos viejos, que tenía aceleración para el desplazamiento y utilizaba un modo de color indexado.

El pseudo efecto rasterizado de la carretera funciona realmente de forma similar al efecto de perspectiva de Street Fighter II , en que deforma una imagen estática para crear la ilusión de 3d. Así es como se hace:

La mayoría de las carreteras rasterizadas comienza con la imagen de una carretera plana. Esto es esencialmente un gráfico de dos líneas paralelas en el suelo perdiéndose en la distancia. A medida que estas líneas se pierden en la distancia, parecen estar más juntas para el espectador. Esta es la regla básica de la perspectiva. Ahora, para dar la ilusión de movimiento, la mayoría de los juegos arcade de carrera tienen rayas en la carretera. Moviendo estas rayas hacia adelante es generalmente o bien logrado con ciclo de color, o bien cambiando la paleta en cada línea. Las curvas y direcciones se hacen desplazando cada línea independientemente de la otra, así como en Street Fighter II.

Abordaremos las curvas y direcciones en el siguiente capítulo. Por ahora, dejémoslas a un lado y concentrémonos en hacer que la carretera parezca desplazarse hacia adelante.

La Carretera más Simple
Piensa en la imagen de carretera descrita arriba: Dos líneas paralelas demarcando los bordes de la izquierda y la derecha de la carretera. A medida que se mueven en la distancia, parecen estar más cerca a los ojos del espectador. Debajo está lo que tratamos de entender:

Lo que no aparece en esta imagen son las marcas de la carretera para dar la impresión de distancia. Los juegos usan rayas iluminadas y oscuras de forma alternada, entre otras marcas de la carretera, para este efecto. Para hacerlo más complejo, definamos una variable "texture position". Esta variable comienza en cero al fondo de la pantalla y se incrementa por cada línea hacia arriba de la pantalla. Cuando está por debajo de una cierta cantidad, la carretera es dibujada en un sombreado. Cuando supera esa cantidad, se dibuja en el otro tono. La variable de posición vuelve a 0 cuando supera la cantidad máxima, causando un patrón repetitivo.

No alcanza con cambiar esto por una cierta cantidad en cada línea, pues entonces verás varias rayas de diferentes colores que no se hacen más pequeñas a medida que la carretera se pierde en la distancia. Esto significa que necesitas otra variables que cambien por una determinada cantidad, lo sumen a la otra variable por cada línea, y luego se sume la ultima al cambio en la posición de la textura.

Aquí hay un ejemplo que muestra, desde el fondo de la pantalla, lo que será el valor Z para cada línea a medida que se pierden en la distancia. Luego de las variables, imprimo lo que se le suma para obtener los valores de la siguiente línea. Nombré los valores DDZ (delta delta Z), DZ (delta Z), y Z. DDZ se mantiene constante, DZ cambia de forma lineal, y Z es el valor de las curvas. Puedes pensar en Z como la representación de la posición Z, DZ lo que mantiene la velocidad de la posición, y DDZ la aceleración de la posición (el cambio en la aceleración). El valor que elegí, cuatro, es arbitrario y conveniente para este ejemplo.

DDZ = 4 DZ = 0 Z = 0 : dz += 4, z += 4
DDZ = 4 DZ = 4 Z = 4 : dz += 4, z += 8
DDZ = 4 DZ = 8 Z = 12 : dz += 4, z += 12
DDZ = 4 DZ = 12 Z = 24 : dz += 4, z += 16
DDZ = 4 DZ = 16 Z = 40 : etc...


Fíjate que DZ es el primero en modificarse, y luego se usa para modificar Z. Para resumir, diremos que te estás moviendo a través de la textura a una velocidad de 4. Eso significa que luego de la primera línea, estarás leyendo la textura en la posición 4. La siguiente línea será 12. Luego,24. Así, de esta manera se lee a través de la textura rápido y más rápido. Por eso nos referimos a estas variables como la posición de la textura (dónde estamos leyendo dentro de la textura), la velocidad de la textura (qué tan rápido leemos a través de la textura), y la aceleración de la textura (qué tan rápido se incrementa la velocidad de la textura).

Un método similar también puede ser utilizado para dibujar curvas y colinas sin demasiados números. Ahora, para hacer que la carretera parezca moverse, sólo cambia dónde comienza la posición de la textura al fondo de la pantalla para cada frame.

Ahora, puedes notar un inconveniente con este truco: la tasa de zoom no es precisa. Esto causa una distorsión a la que me referiré como el "efecto harina de avena". Es un efecto de deformación presente en los primeros juegos como OutRun donde los objetos, incluyendo las rayas en la carretera, parecen desacelerar a medida que se mueven hacia afuera del centro de la pantalla.

Este método para encontrar el valor de Z tiene otra desventaja: No es fácilmente predecible el valor correspondiente a cada distancia, especialmente cuando incluimos las colinas. Aprenderemos un método más avanzado al que llamaré el "Z-map". Ésta es una tabla que calcula la distancia Z para cada scanline de la pantalla. Pero primero, necesitamos un poco más de matemática...

Un Desvío Matemático: Proyección de Perspectiva 3d
Hay diversas formas de encarar el problema del efecto "harina de avena". Sin embargo, se necesitan ciertas matemáticas 3d tradicionales para hacer esto posible. Lo que necesitamos es una forma de trasladar las coordenadas 3d de forma que éstas se puedan ajustar a una superficie 2d.

En la imagen de arriba, un globo ocular (abajo a la izquierda) está mirando, a través de la pantalla (la línea vertical azul), un objeto en nuestro mundo 3d ("y_world"). Este ojo está a una distancia "dist" de la pantalla, y a una distancia "z_world" del objeto. Ahora, una cosa que podrías haber notado si pensanste en la geometría o trigonometría es que no hay uno sino dos triángulos en la imagen. El primero es el más grande, del ojo sobre el suelo del lado derecho y arriba al objeto al que estamos observando. El segundo triángulo lo he coloreado amarillo. Está desde el ojo hacia la parte de la pantalla donde veremos nuestro objeto, debajo del suelo , y detrás.

Las hipotenusas de ambos triángulos (la línea desde el ojo al objeto) están en el mismo ángulo incluso aunque una sea más larga que la otra. Son esencialmente el mismo triángulo, pero el menor está reducido. Lo que esto implica es que el radio de los lados horizontales como los verticales debe ser el mismo! En términos matemáticos:

y_screen/dist = y_world/z_world

Lo que necesitamos hacer ahora es acomodar la ecuación para obtener el valor de y_screen. Eso nos da:

y_screen = (y_world*dist)/z_world

En resumen, para encontrar la coordenada y de un objeto en la pantalla, tomamos la coordenada y world, la multiplicamos por la distancia a la que estamos de la pantalla, y luego se divide eso por la distancia a la que se encuentra en el mundo. Por supuesto, si sólo hacemos eso, el centro de nuestra vista estará en la esquina superior izquierda de la pantalla! Sólo iguala y_world a 0 para verlo. Lo que podemos hacer para centrarla es sumarle la mitad de nuestra resolución de pantalla al resultado. Esta ecuación también puede ser simplificada un poco asumiendo que nuestras narices están justo sobre la pantalla. En tal caso, dist=1. Por lo tanto, la ecuación final es:

y_screen = (y_world/z_world) + (y_resolution/2)

Hay una relación entre los radios y el ángulo de visión, así como también el escalar la imagen de forma que su resolución sea neutral, pero no necesitaremos realmente nada de eso para arreglar el problema de nuestra carretera. Si eres curioso, intenta mirar el diagrama que está visto desede arriba: el ángulo al borde de la pantalla es nuestro campo de visión y se mantiene la misma relación!

Más Matemática: Agregando el Campo-de-Visión la Proyección 3d
Ahora, esto es extremadamente innecesario para la mayoría de los casos. Sin embargo, resulta útil para hacer que los parámetros de proyección sean independientes de la resolución, o para objetos que necesitan rotar, o incluso para integrar nuestro motor con efectos 3d reales.

Volvamos a la fórmula de proyección original. La distancia "dist" que explicamos arriba ahora será llamada "scaling":

y_screen = (y_world*scaling)/z_world + (y_resolution/2)

La idea es que necesitamos escalar todos los puntos de la pantalla por algún valor que permite que aquellos puntos que están dentro de un determinado campo-de-visión (FOV) permanezcan visibles. Necesitarás una constante para el valor x del FOV y otra para el valor y.

Como ejemplo, asumamos que estamos trabajando en una resolución de 640x480 y queremos un FOV de 60 grados. Hemos visto un diagrama de proyección 3d vista de forma lateral. Para esto, en su lugar echemos un vistazo a la vista cenital del espacio de proyección:

Una forma de pensar acerca del problema es que si un objeto está en el borde derecho de nuestro FOV, tiene que aparecer en la pantalla en x=640 (ya que estamos en 640x480). Mirando el diagrama, nuestro FOV se puede dividir en dos triángulos rectángulos donde el ángulo de cada uno es fov_angle/2 (a/2). Y debido a que nuestro FOV es un cono, un objeto está en el borde derecho de su FOV si su x=R*sin(a/2) y z=R*cos(a/2), donde R es cualquier valor del radio que querramos. Podríamos también hacer que R=1. Y necesitamos que el objeto aparezca en x_screen=640. Eso nos da esto (comenzando por la fórmula de proyección básica):

x_screen=640   fov_angle=60   y_world=sin(60/2)   z_world=(60/2)   x_resolution/2=320   scaling=?

x_screen = (y_world*scaling)/z_world + (x_resolution/2)
640 = (sin(30)*scaling/cos(30)) + 320
320 = tan(30)*scaling
320/tan(30) = scaling

En términos generales: scaling = (x_resolution/2) / tan(fov_angle/2)

Hemos reemplazado a/2 por 30 (la mitad de 60 grados), reconociendo que sin/cos = tan, y voilá! Debemos ser capaces de probar esto colocando un objeto en el borde derecho del campo-de-visión, estableciendo estos valores en la ecuación de proyección original, y asegurándonos que el valor X termina como 640. Por ejemplo, un punto (x, z) en (20, 34.64) caerá en X=640 porque 20 es 40*sin(30) y 34.64 es 40*cos(30).

Nota que tendrás diferentes valores del FOV para el horizontal (x) y el vertical (y) para un monitor estándar o panorámico con orientación horizontal.

Una Carretera Más Precisa - Usando un Z Map
Lo que queremos hacer para solucionar nuestro problema de perspectiva es precomputar una lista de distancias para cada línea de la pantalla. Resumiendo, el problema es cómo describir un plano en 3d. Para entender cómo funciona, primero piensa en el equivalente en 2d : una línea! Para describir una línea horizontal en 2d, dirías que para cada par (x, y) la coordenada y es la misma. Si extendemos esto a 3d, se convierte en un plano: para cada distancia X y Z, el valor de Y es el mismo! Cuando se trata de una superficie horizontal plana, no importa cuán lejos está de la cámara, el valor de y es siempre el mismo. Igualmente, no importa a cuánto está el punto de la izquierda o de la derecha, la coordenada y permanecerá igual. Volviendo al asunto de darnos cuenta de la distancia de cada línea de la pantalla: llamaremos esto un Z Map. Calcular el Z Map es sólo asunto de reorganizar la fórmula de proyección 3d para hallar un valor de Z para cada valor Y de la pantalla!

Primero, toma la ecuación de la última sección:

Y_screen = (Y_world / Z) + (y_resolution / 2)

Ahora, ya que obtuvimos Y_screen (cada línea), acomoda la ecuación de forma tal que encontremos la Z:

Z = Y_world / (Y_screen - (height_screen / 2))

Y_world es básicamente la diferencia entre el suelo y la altura de la cámara, que será negativa. Esto aplica para cada línea porque, como describimos en el párrafo de introducción, por ahora estamos interesados en una carretera llana. Además de verse mucho más precisa y evitar el "efecto de harina de avena", tiene la ventaja de que es fácil de computar cuál es la distancia máxima a dibujar.

La carretera es mapeada en la pantalla leyendo este buffer: Para cada distancia, debes saber qué parte de la textura de la carretera pertenece a allí a partir de cuántas unidades de franja o pixel de la textura requiere.

Aunque ahora sabemos la distancia de cada fila de la pantalla, puede también ser útil cachear ya sea la anchura de la carretera o el factor de escalado para cada línea. El factor de escala sólo sería la inversa de la distancia, ajustado para que el valor sea 1 en la línea donde el vehículo del jugador pase la mayor parte del tiempo. Este valor puede entonces ser utilizado para escalar los sprites da una línea dada, o para hallar la anchura de la carretera.

Dirección y Curvas

Haciéndola Curva
Para curvar una carretera, sólo necesitas cambiar la posición del centro de cada línea en una forma de curva. Hay un par de formas de hacer esto. La primera es hacerlo de la forma en la que se hicieron las posiciones Z en "La Carretera más Simple": con tres variables. Es decir, comenzando en el fondo de la pantalla, la cantidad que el centro de la carretera dobla hacia la izquierda o derecha por línea se incrementa continuamente. Así como para leer la textura, podemos referirnos a aquellas variables como la posición del centro de la línea (curva), la velocidad de la curva, y la aceleración de la misma.

No obstante, hay algunos problemas con este método. Uno es que las curvas-S no son convenientes. Otra limitación que tiene entrar en la curva y que tambien se encuentra al salir de ésta: la carretera se curva, y simplemente se endereza.

Para mejorar la situación, introduciremos la idea de segmentos de carretera. Un segmento es una partición la cual es invisible al jugador. Piensa en ello como una división horizontal invisible que establece la curva de la carretera por encima de esa línea. En cualquier momento, uno de estos segmentos divisores está al fondo de la pantalla y otro viene desplazándose hacia el fondo en una tasa que se incrementa continuamente. Lllamaremos al que se encuentra al fondo el segmento base, ya que establece el inicio de la curva de la carretera. Aquí se ve cómo funciona:

Cuando comenzamos a dibujar la carretera, la primero que hacemos es mirar el punto base y establecer los parámetros para dibujar en consecuencia. Cuando una curva se aproxima, la línea del segmento comenzaría en la distancia y viene hacia el jugador como cualquier otro objeto de la carretera, con la excepción de que necesita descender por la pantalla en una tasa continua. Es decir, para una velocidad específica a la que el jugador está viajando, el segmento divisor desciende por la pantalla a algunas líneas por frame. O, si está utilizando un Z-Map, unas tantas entradas del z-map por frame. Si el segmento fuera a 'acelerar' hacia el jugador tal como lo hacen los objetos 3d en la pista, la carretera oscilaría salvajemente.

Veamos cómo funciona todo esto. Suponiendo que la línea del segmento para una curva hacia la izquierda está a medio camino en la carretera y el segmento base es sólo una carretera recta. A medida que la carretera es dibujada, no empieza a curvarse hasta que no "impacte" con el segmento de "curva izquierda". Luego la curva de la carretera comienza a cambiar a la tasa especificada para ese punto. A medida que el segmento que se mueve llega al fondo de la pantalla, se convierte en el nuevo segmento base y el que previamente era el base vuelve a la cima de la carretera.

Debajo se muestran dos carreteras: Una es una recta seguida por una curva a izquierda, y la otra es una curva a izquierda seguida por una recta. En ambos casos, la posición del segmento está a medio camino en el Z Map (o, a medio camino en la pantalla). En otras palabras, la carretera comienza a curvarse o enderezarse a medio camino en la carretera, y la cámara está entrando en la curva en la primera imagen y saliendo de ésta en la segunda.

Y esta es la misma técnica y la misma posición del segmento aplicadas a una curva-S:

La mejor forma de realizar un seguimiento de la posición del segmento es en términos de dónde está en el Z Map. Es decir, en lugar de asociar la posición del segmento a una coordenada y de la pantalla, asóciala a una posición en el Z Map. De esta manera, aún comenzará en el horizonte de la carretera, pero será más capaz de manejar las colinas. Nota que en una carretera llana ambos métodos de realizar un seguimiento de la posición del segmento son equivalentes.

Ilustrémoslo con algo de código:

current_x = 160 // La mitad de una pantalla de 320 de ancho
dx = 0 // Cantidad de la curva, constante por segmento
ddx = 0 // Cantidad de la curva, cambia por línea

for each (línea de la pantalla del fondo hacia arriba):
  if (la línea de la posición del Z Map en pantalla es menor que segment.position):
    dx = bottom_segment.dx
  else if (la línea de la posición del Z Map en pantalla es mayor que segment.position):
    dx = segment.dx
  end if
  ddx += dx
  current_x += ddx
  this_line.x = current_x
end for

// Mueve los segmentos
segment_y += constant * speed // Constant asegura que el segmento no se mueva tan rápido
if segment.position < 0 // 0 es el más cercano
  bottom_segment = segment
  segment.position = zmap.length - 1 // Envía la posición del segmento a una distancia más lejana
  segment.dx = GetNextDxFromTrack() // Busca la cantidad de la siguiente curva
end if


Una gran ventaja de hacer las curvas de esta forma es que si tu tienes una curva seguida de una recta, puedes ver cómo la recta viene hacia ti luego de la curva. De esta manera, si tienes una curva de seguida de otra curva en la dirección opuesta (o incluso una curva más cerrada en la misma dirección), puedes ver la suguiente fracción de pista que se aproxima sobre la curva antes de que te la encuentres.

Para completar la ilusión, necesitas tener un gráfico del horizonte. A medida que la curva se aproxima, el horizonte no cambia (o hace un scroll muy suave). Luego cuando la curva está completamente dibujada, asume que el auto está yendo de forma curvada, y el horizonte realiza un scroll rápidamente en la dirección opuesta a la que la curva apunta. A medida que la curva se vuelve a enderezar, el fondo continua desplazándose hasta que la curva se completa. Si estás usando segmentos, puedes solamente desplazar el horizonte de acuerdo a las configuraciones del segmento base.

Fórmula General de Curva
Hay una observación interesante que podemos hacer acerca de la técnica de curva detallada en la sección "La Carretera más Simple". Dicha observación es más matemática que el material de arriba, y puede ser totalmente ignorada tanto como si el motor gráfico no tiene que ser independiente de la resolución o si utiliza la técnica de "segmentos proyectados en 3d" discutida en el capítulo de colinas.

Viendo el ejemplo de curva utilizando la "Z" de la sección "La Carretera más Simple", podemos ver que la posición z (o la posición x) de una línea dada es la suma de una sucesión incremental de números (ej. 1 + 2 + 3 + 4). Esto es lo que llamamos una serie aritmética, o progresión aritmética. En lugar de 1 + 2 + 3 + 4, una curva más pronunciada se puede producir sumando 2 + 4 + 6 + 8, o 2*1 + 2*2 + 2*3 + 2*4. El "2" en este caso es la variable segment.dx de arriba. Puede también ser factorizado para obtener 2(1 + 2 + 3 + 4)! Ahora todo lo que se debe hacer es hallar una fórmula para describir 1 + 2 + ... + N, donde N es el número de línea que conforman la curva. Resulta que la suma de una serie aritmética es igual a N(N+1)/2. Entonces, la fórmula se puede escribir como s = A * [ N(N+1)/2 ] donde A es la pronunciación de la curva y s es la suma. Esto además se puede modificar para agregar un punto de inicio, por ejemplo, el centro de la carretera al fondo de la pantalla. Si llamamos esto 'x', tenemos ahora s = x + A * [ N(N+1)/2 ].

Tenemos ahora una fórmula para describir nuestra curva. La pregunta que queremos resolver es, "dado un punto inicial x y N líneas de la curva, cuánto debería valer A para que la curva alcance la posición x 's' al terminar?" Acomodando la ecuación para despejar A obtenemos A = 2(s - x)/[n(n+1)]. Esto significa que la pronunciación de la curva de una curva dada puede ser almacenada en términos de la posición X del punto final, haciendo al motor gráfico independiente de la resolución.

Direccionamiento Con Estilo de Perspectiva
Es mucho menos interesante tener un juego donde al doblar, sólo se mueve el sprite del auto. Por lo tanto, en lugar de mover el sprite del auto del jugador, mantenlo en el centro de la pantalla y mueve la carretera-- más importante aún, mueve la posición del centro de la línea al frente (fondo) de la pantalla. Ahora, quieres asumir que el jugador estará viendo la carretera siempre, por lo que haz que ésta termine en el centro de la pantalla. Para esto necesitarás una variable para el ángulo de la carretera. Por lo tanto, calcula la diferencia entre el centro de la pantalla y la posición del frente de la carretera, y divide eso por la altura del gráfico de la carretera. Esto te dará la cantidad a mover el centro de la carretera cada línea.

Sprites y Datos

Colocando y Escalando los Objetos
Los sprites se deben dibujar desde atrás hacia adelante. Esto a menudo se conoce como el Algoritmo del Pintor. Para hacerlo, tendrás que mantener previamente el valor de dónde se debe dibujar cada objeto en la pantalla, y luego dibujarlos en un paso diferente. Yo lo hago de la siguiente forma: A medida que voy por el Z Map al dibujar la carretera, me gusta también anotar en ese momento con qué línea de la pantalla se debe asociar cada sprite. Si mantienes tus sprites ordenados por Z, esto es trivial: Cada vez que un nuevo valor del Z Map es leído, verifica si la posición Z del siguiente sprite es más cercana a la cámara que la del sprite actual, o si es igual. Si es así, registra esa posición Y del sprite en pantalla como perteneciente a la línea actual. Luego verifica el siguiente sprite de la misma manera. Sigue haciendo esto hasta que saques de la lista un sprite que tenga una posición Z más lejana que la actual.

La posición X del objeto debe ser registrado con relación al centro de la carretera. La forma más sencilla para posicionar el sprite horizontalmente es sólo multiplcarlo por el factor de escalado para la línea actual (el inverso de Z) y sumarlo al centro de la carretera.

Almacenando Datos de la Pista
Cuando hice mi primer demo de carretera, almacené la información del nivel como una lista de eventos que ocurrirían en distancias específicas. Las distancias son, por supuesto, en términos de unidades de posición de textura. Los eventos consistirían en comandos para comenzar y frenar curvas. Ahora, lo que puedo decir, es que la velocidad a la que la carretera comienza y deja de curvarse es arbitraria. La única regla parece estar correlacionada con la velocidad del vehículo de jugador.

Si, no obstante, estás utilizando un sistema segmentado, puedes usar una lista de comandos. La distancia que cada comando requiere es equivalente a cuán rápido desciende en pantalla el segmento invisible. Esto también te deja crear un formato de pista que trabaje en un tile map, para representar alguna geografía realista de la pista. Es decir, cada tile podría ser un segmento. Una curva pronunciada podría doblar la pista 90 grados, mientras una curva más suave lo haría en 45 grados.

Texturizando la Carretera
Ahora, probablemente quieras una gráfica de textura real en tu carretera en lugar de las líneas alternadas y todo eso que tienes hasta ahora. Hay un par de formas de hacer esto. Una forma fácil y barata es la siguiente: tienes un par de texturas para la carretera (para el efecto de líneas alternadas). Cuando cada línea horizontal de la carretera es dibujada, estira la textura para ajustarla al ancho de esa línea. O, si no lo puedes hacer, toma una línea de una de dos bitmaps de la carretera completa (como Outrunners).

Si quieres que la carretera se vea más precisa, haz que el valor Z para cada línea corresponda con un número de fila en un gráfico de textura. Voila! Un carretera texturizada!

Sin embargo, si sólo quieres franjas de colores alternadas, la respuesta es incluso más simple-- especialmente cuando se usa punto fijo. Para cada Z, haz que uno de los bits represente el tono de la carretera (oscuro o claro). Luego, sólo dibuja el patrón de carretera apropiado o los colores para ese bit.

Colinas

Variedades de Colinas
Parece que hay casi infinitas formas de producir efectos de colina. Estos efectos tienen un amplio rango de precisión geométrica, con algunas de las técnicas menos precisas siendo más convincente que otras. Aquí examinaremos dos posibles métodos.

Colinas Falsas
Luego de mucha experimentación, he dado con un método flexible para "falsificar" colinas que utiliza poco en términos de cálculos. Adicionalmente, mantiene de forma precisa los objetos que están detrás del horizonte. Es un efecto de escala y distorsión que estira y contrae verticalmente la carretera. Para dibujar la curvatura de las colinas, se utiliza el mismo truco de suma usado para dibujar las curvas.

Así es cómo se hace: Primero que nada, el bucle de dibujo comenzaría al comienzo del Z Map (lo más cercano) y pararía cuando alcance el final (lo más lejano). Si decrementamos en 1 la posición de dibujo en cada línea, la carretera se dibujará llana. Sin embargo, si decrementamos la posición de dibujo en 2, duplicando las líneas, la carretera será dibujada dos veces más alta. Finalmente, variando la cantidad que decrementamos la posición de dibujo en cada línea, podemos dibujar una colina que comienza llana y se curva hacia arriba. Si la siguiente posición de dibujo está a más de una línea de diferencia de la posición de dibujo actual, la línea del Z Map actual es repetida hasta que lleguemos a ese valor, produciendo un efecto de escalado.

Las pendientes son similares: Si la posición de dibujo es incrementada en lugar de decrementada, se moverá debajo de la última línea dibujada. Por supuesto, las líneas que están debajo del horizonte no serán visibles en-pantalla-- sólo las que están 1 o más píxeles arriba de la última línea deben ser dibujadas. Sin embargo, vamos a querer aún mantener un registro o seguimiento de los objetos que están debajo del horizonte. Para hacerlo, mantén la posición Y en pantalla de cada sprite a medida que recorres el Z Map. Puede ser útil hacer el Z Map más grande que lo necesario para una carretera llana. De esta forma, cuando el buffer se expanda, no se volverá tan pixelada.

Ahora, tenemos que mover el horizonte para convencer al jugador. Me gusta usar un background del estilo de Lotus, en donde el horizonte no consiste sólo en una línea de horizonte (skyline), sino también un gráfico de un terreno distante. Cuando la colina se curva hacia arriba (elongando la vista), el horizonte debe moverse hacia abajo ligeramente con relación al tope de la carretera. Cuando la colina se curva hacia abajo a medida que la cámara avanza sobre la cresta de ésta (acortando la vista), el horizonte debe moverse hacia arriba.

Así es como luce el efecto para una cuesta arriba y hacia abajo-- menos el gráfico del horizonte por supuesto:

Pros

• Barato en términos de cálculos: no son necesarias la multplicaciones o divisiones
• Los objetos en la parte trasera de la colina son respaldados
• El ángulo de la vista parece seguir al jugador sobre las colinas

• Una geometría 3d precisa es imposible
• Es necesario retorcer la carretera para crear un efecto convincente

Llevando a las Carreteras Rasterizadas Más Allá

No obstante, puedes queres exagerar el efecto para obtener una carretera más dramática. Una cosa que se puede hacer con algunas de aquellas fórmulas es usar valores altos para ddx o ddy, pero sin permitir que dx o dy excedan un valor sensato. Y un usuario en YouTube, Foppygames, ha descubierto otro truco para obtener curvas más exageradas a partir de dichas fórmulas: multiplicar el valor de dx o dy por el valor z para cada línea! Esto hace más severa a la curva en la distancia que adelante, y crea un efecto muy convincente.

Además, la experimentación no acaba ahí. De hecho, lo mejor de estos motores es que no hay una forma "correcta" de hacerlo. Lo que sea que cree curvas y deformaciones que sean agradables al ojo está permitido! En mis primeros motores, usé una tabla de búsqueda sinusoidal para curvar la carretera.

Puedes también usar la multiplicación: Para doblar la carretera a la derecha, puedes multiplicar la posición x por, por ejemplo, 1.01 cada línea. Para moverla a la izquierda la misma cantidad, podrías multiplicarla por 0.99, o 1/1.01 (recíproco de 1.01). Sin embargo, armado con el conocimiento de que varios procesadores antiguos no tenían multiplicación o eran muy lentos en ello, decidí usar la técnica de acumulación porque sólo usa suma. Parecía la forma más "auténtica" de curvar la carretera.

Algunos juegos, como OutRun, utilizan incluso un sistema de spline simple-- al menos a juzgar por el gran port hecho con ingeniería inversa y open-source en C++, Cannonball.

Por lo tanto, juega y experimenta, y mira qué técnica te gusta más!

...o, lee la descripción de un truco más inteligente que mezcla polígonos 3d, es casi tan rápido, es incluso más convincente, y puede ser presentado con el mismo hardware "oldschool" de rasterizado. Intrigado?

Segmentos Proyectados en 3D Real

Segmentos Proyectados en 3d vs. Carreteras Rasterizadas
Además de lo bien que lucen las carreteras rasterizadas, éstas pueden ser más impresionantes incluyendo una forma simple de renderizado de polígonos. Esta forma de renderizar puede realmente ser aplicada utilizando el mismo hardware de rasterizado limitado. Sin embargo, incluye más cálculos.

Este truco es conocido por haber sido usado en juegos tales como Road Rash y Test Drive II: The Duel. Aquí está cómo se hace: La pista está hecha de segmentos poligonales. No obstante, en lugar de moverse en un espacio 3d completo, aún lo hace moviéndose hacia la cámara. Para las curvas, la carretera aún se dobla a izquierda y derecha en una forma casi idéntica a la rasterizada: no hay rotación real cuando se va por una curva como lo habría en un motor de puros polígonos.

Aquí hay un resumen:

• Ya que todavía estamos simulando curvas y ángulos de carretera, eso significa que hacer cálculos de rotación costosos aún no será necesario.
• La carretera es esencialmente una franja de cuadrados: cada sección de la pista está unida a la siguiente. Esto quiere decir que podemos calcular si parte de la carretera está visible o no basándonos sólo en su posición Y en pantalla en forma relativa a su vecino anterior.
• La relación de estos cuadrados con otros jamás cambiará. Es decir, el ángulo nunca cambia realmente, por lo que los cuadrados están siempre y automáticamente ordenados por Z.

La Carretera 3D Básica
Primero, divide la carretera en cuadrados poligonales. Cada uno de éstos se llamará segmento. Al igual que un segmento en una carretera absolutamente resterizada, cada segmento aquí aún tiene una cantidad de curva (ddx), e incluso una cantidad para la colina (ddy) o una posición y que determina cuán alta está. Por supuesto, estos segmentos pueden tener también otros atributos como cambios en el terreno.

Debajo hay una carretera segmentada hecha de algunos pocos polígonos por lo que podemos ver fácilmente los límites entre los segmentos y cómo afecta esto a la curvatura de la carretera:

Al renderizar, primero encuentra la ubicación y de la pantalla de cada segmento tridimensional al usar la fórmula screen_y = world_y/z. O, si la división en demasiado lenta, puedes hallar la altura sobre el suelo de un segmento dado multiplicando la altura del segmento por el factor de escalado para esa línea. Eso podría luego ser sustraída de un Z-Map inverso (este mapa sería: para cada posición z de una carretera llana, cuál es su y?) para hallar la posición final en pantalla.

Luego, podrías interpolar linealmente la anchura de la carretera y la textura (si lo deseas) entre aquellas alturas. Decidir qué segmentos tridimensionales dibujar y cuáles no puede ser determinado fácilmente: Desde el frente hacia atrás en la pantalla, un segmento 3d cuyo screen_y es proyectado más bajo que el último segmento dibujado no se mostraría (sin embargo, sus sprites podrían aún ser visibles porque éstos se mantienen-- tenlo en cuenta).

Desplazando la Carretera
Ahora, también necesitamos aprender cómo desplazar estos segmentos. Mueve todo el desorden de polígonos que conforman la carretera hacia la cámara. A medida que el polígono del segmento frontal pasa hacia la cámara, mueve toda la carretera de nuevo a su punto de partida de forma que haga un bucle. Desplazamos hacia arriba un segmento, y cuando éste sea alcanzado, movemos la carretera hacia atrás y extraemos nuevos datos.

Pero hay un último detalle muy importante: digamos que la carretera es una curva pronunciada. Podrías haber notado que a medida que vas por esta curva poligonal, ésta se agita cuando cruzas el límite del segmento y la carretera se reestablece posteriormente. Una cosa obvia que ocurre y que causa esto es que cuando atraviesas un segmento sesgado, el centro de la cámara relativo a la carretera cambia. Es decir, cuando llegues al final de ese segmento, la carretera ya no estará centrada. Es como si estuvieras conduciendo en la carretera en un ángulo. Podrías estar tentado de reparar esto moviendo la carretera hasta centrarla tal como las posiciones x de los objetos son interpoladas linealmente.

Sin embargo, esto está mal y no resuelve completamente nuestro problema: Si la carretera fuese sesgada en línea recta, estaría bien. El problema es que nuestra carretera se curva, por lo que los polígonos en la distancia aún no está alineados! Otra forma de pensar acerca de esto es la siguiente: Estamos aproximándonos a una curva usando segmentos poligonales. Lo que queremos es que la forma de la curva sea más o menos constante incluso cuando se desplaza.

Jake de codeincomplete.com tiene una gran solución para esto. En lugar de cambiar la posición x de la carretera cuando te mueves a través del segmento, que hay si cambiamos el valor dx inicial de 0 a algo que mantenga la carretera en línea a medida que te mueves por el segmento? La fórmula usada es esta:

dx = -porcentaje_de_segmento_atravesado * ddx

Este porcentaje tiene que ir de 0 a 1.0 y hacia atrás cuando la cámara cruza la cámara.

En términos matemáticos, hacer esto hace a la X de la carretera una función de su Z. En otros términos, estamos manteniendo la curva en la misma forma a pesar de cómo se desplazan los puntos que la aproximan. El segmento más frontal es "estirado en posición" con el resto de la carretera, lo que significa que las posiciones X de los segmentos subsecuentes están correctamente ubicados. Puedes verlo claramente si lo pruebas con una carretera hecha de algunos polígonos. Esto resuelve los siguientes problemas a medida que el segmento es atravesado (asumiendo que la forma de la curva no cambia):

• Se mantiene el centro de la carretera (posición x) constante
• Ajusta dx de forma que el siguiente segmento comience en una ubicación x apropiada independientemente de la posición de desplazamiento de la carretera

El siguiente video demuestra esta técnica. He utilizado algunos segmentos y una curva muy pronunciada para demostrar cómo luce. Observa que a medida que los polígonos se mueven hacia el jugador, describen una curva perfecta. Es más notorio si observas el lado derecho de la carretera.

Colocando Sprites
Los sprites en este segmento 3D aún deberían ser mostrados y recortados correctamente -- asumiendo que estás haciendo un renderizado personalizado y no utilizas un Z-buffer. Podemos realmente dibujar los sprites como el último paso: Si un sprite está en un segmento completamente visible, no necesita ser recortado ya que se encuentra unido al suelo, que es nuestro único polígono.

Pero si un sprite se encuentra en un segmento que es invisible o parcialmente visible, podemos recortarlo fácilmente. Primero, encuentra la parte superior del sprite. Luego, cada línea del sprite será dibujada hasta que toque la posición Y en pantalla del último segmento visible. Es decir, si hay un segmento detrás del sprite que se supone debe cubrir parte de este, paras de dibujar ese sprite cuando tocas esa línea. Y si la parte superior del sprite está debajo de la posición Y del último segmento, el sprite no será visible en absoluto y será ignorado.

Variaciones y Tecnologías de Renderizado
Ahora, debido a que estamos hablando del término polígono, puedes estar tentado de pensar que necesitas rutinas de renderizado poligonal para lograrlo. Utilizando tecnologías como OpenGL o una rutina de dibujo trapezoidal simple definitivamente puedes hacerlo. Incluso el hardware de sprites y tiles 2d puede lograrlo perfectamente.

Observa que el comienzo y final de cada segmento de la carretera son perfectamente horizontales. Esto significa que siempre comienzan y terminan en una scanline específica. De la misma forma en que la carretera completamente pseudo 3d es renderizada en hardware para tiles desplazando el gráfico de la carretera plana a medida que está siendo dibujado, podemos hacer exactamente lo mismo con los segmentos 3D. Para mayor información, revisa la sección llamada Hardware Dedicado para Carreteras. Aunque habla de harware arcade diseñado desde un principio para lograr efectos de carretera, la misma técnica puede ser lograda con sistemas básicos de sprites/tiles 2D, desplazando el gráfico de la carretera verticalmente como también horizontalmente.

Más Información acerca de Segmentos Proyectados en 3D
Puesto que el prototipo que utilizo en este artículo se encuentra descontinuado, te enviaré al increíble tutorial de Code inComplete si estás interesado en más detalles sobre esta técnica.

Pros

• Se puede utilizar geometría 3D real para las colinas, añadiendo la mayor cantidad de detalle posible
• El sistema es más consistente: No es necesario cambiar el terreno y el ancho de la carretera utilizando una técnica separada

• Se requieren más cálculos
• Se debe utilizar una cantidad decente de segmentos o la carretera se verá mordida y poligonal

Mejoras

Múltiples Carreteras
La mayoría de los juegos de carreras arcade manejan múltiples carreteras a la vez. Aunque la razón más obvia para hacerlo es para tener más de una carretera en pantalla, se pueden lograr también otros efectos. Por ejemplo, OutRun usa más de una carretera para formar su autopista de seis carriles. Esto le permite al juego ensanchar y ajustar la carretera fácilmente, así como también una bifuración convincente. Esto lo logran superponiendo las dos carreteras y dándole una prioridad de dibujo una sobre otra. Aquí está el conocido inicio de OutRun tanto con las dos carreteras como con una (mira a la derecha de los arbustos):

Además, incluso más dramático, debajo está la autopista cuando las dos carreteras están superpuestas para formar seis carriles, con la segunda carretera como sin ella:

Efectos Relacionados

Entonces, cómo se desplaza a izquierda y derecha? Utilizando sólo una variación de la curva en perspectiva: A medida que el jugador se mueve a la izquierda/derecha, el gráfico del suelo se distorsiona. Luego del desplazamiento de algunos pixeles, el suelo "restaura" su posición. Así es como parece que se desplaza infinitamente hacia izquierda y derecha.

Casos de Análisis

Si quieres leer más, puedes revisar la conversación con el autor original en AtariAge aquí.

Las Carreteras en la Commodore 64
Esta información es cortesía de Simon Nicol, quien encontró una gran técnica para carreteras rápidas en la C64.

Primero, algunos conocimientos previos: En varias consolas, se puede hacer una carretera en pseudo-3d dibujando una carretera recta con tiles y scrolling por línea para que parezca curvarse. No obstante, esto resultó ser demasiado lento para un juego con tasa de fotogramas completa en la Commodore 64.

En su lugar, el motor de Simon utiliza el modo mapa de bits (bitmap) de la C64 y un algoritmo de relleno rápido. Este algoritmo utiliza código automodificable para acelerar los dibujos en pantalla: Cada línea es una serie de almacenamientos por pixel que especifica una dirección en la memoria de video. En el punto en donde tiene que cambiar el color, se altera el código. El comando de almacenar (store) se convierte en un comando cargar(load), y lo que era la dirección de almacenamiento se convierte en el número literal del nuevo color.

Una de las mayores ventajas de esta técnica es que las técnicas de multiplexado de sprites para mostrar más de ocho sprites en pantalla aún se pueden utilizar. Según el propio Simon: "Desplazar el scroll horizontal para obtener un efecto rasterizado estable implicaría manipular el registro $D011. De lo contrario, el interruptor IRQ en $D012 parpadearía mucho según el número de sprites en esa línea en particular. Para tener una suerte de suavizado en pantalla se debería bloquear el procesador para obtener el tiempo justo, o no utilizar los gráficos en pantalla y cambiar sólo el color del borde. Esto debería ser sólido y libre de parpadeos, pero no habría carretera visible en pantalla puesto que tendría que ser desactivada. Estos cambios suaves en los colores del borde por línea fueron utilizados persiguiendo el interruptor por la pantalla, y podía además ser utilizado para 'esperar' donde se mostraría la parte superior de la pantalla. Esto se llamó espera de $D011 o a veces FLD por Flexible Line Distancing o Distanciamiento de Línea Flexible (la técnica usada para eliminar las líneas malas del VIC).

Otros Motores

Power Drift

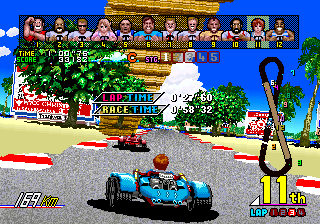
Power Drift es interesante debido a que es uno de los pocos juegos que conozco que utilizan 3d basado en sprites. Cada trozo de la pista es un sprite pequeño del suelo borroso, y la cámara aérea es la forma que tiene Sega de presumirlo. No tengo pruebas, pero creo que juegos como F1 Exhaust Heat y RadMobile usan un sistema similar. También vale la pena observar que la cabina de lujo de Power Drift se inclinaba en casi 45 grados, haciéndolo algo importante para colocarse ese cinturón de seguridad de una vez. Capturas de pantalla de system16.com.

Racin' Force

Racin' Force fue una ingeniería inversa del intrépido Charles MacDonald. Racin' Force corre en la placa Konami GX, que cuenta con una placa hija con capacidades de motor de voxel. Este hardware está basado en otro más antiguo que podía dibujar sólo un plano al estilo Mode 7 de la SNES. Fue extendido para hacer un relieve a través de esta técnica astuta: Proyecta no sólo el tilemap en un plano 3d llano, sino también la información de la altura por cada pixel en su propio plano 3d separado. Luego, por cada pixel de la pantalla, busca este información en el relieve proyectado, y extruye cada pixel hacia arriba lo necesario. Capturas de pantallas de system16.com.

Exploración Adicional

• Cannonball: Port open source de OutRun
• Juego de carreras en JavaScript de Code inComplete

Asuntos del Código

La multiplicación de punto fijo es más complicada que la suma. En esta operación, se multiplican los dos números y luego se desplaza a la derecha aunque varios bits están reservados para la parte decimal. Debido al desbordamiento, a veces puedes necesitar desplazar antes de la multiplcación en vez de después. Mira "Interpolación Lineal Rápida" para un ejemplo de producto de punto fijo.

Rotación de un Punto
x' = x*cos(a) - y*sin(a)
y' = x*sin(a) + y*cos(a)
Brevemente mencionada en el tutorial como una operación costosa, aquí está la fórmula básica de rotación de un punto. Como puedes ver, son al menos dos búsquedas a la tabla, 4 multiplicaciones, y dos sumas, pero los valores del seno y coseno se pueden reutilizar para cada punto. Rotar para obtener las colinas implica rotar las coordenadas Z e Y, en lugar de las coordenadas X e Y. Para hallar la derivada de esta fórmula, mira Rotación de Ejes.

Evita la División
En lugar de dividir por la z de un objeto en la fórmula estándar de proyección, puedes tomar ventaja de algunas propiedades de la carretera para acelerar los cálculos. Digamos que tienes la posición z e y de un segmento 3d, y quieres encontrar a qué línea de la pantalla pertenece. Primero, lee por el z-map hasta obtener la posición z del segmento 3d. Luego, multiplica la altura del segmento por el valor de escala correspondiente. El resultado es el número de pixeles arriba de la carretera a los que pertenece el segmento.

Usa Z como Valor de Escalado
Las rutinas de escalado consisten en reducir o acelerar la velocidad a la que lee la rutina de dibujo los datos gráficos. Por ejemplo, si establecieras la velocidad de lectura a la mitad, se dibujaría un sprite del doble del tamaño. Esto se debe a que por cada vez que se dibuja un pixel, la posición de lectura en los datos del sprite sólo se incrementa la mitad, haciendo que la posición de lectura se incremente en un número entero cada dos pixeles.

Generalmente, una rutina de escalado tiene parámetros como x, y, y el facto de escalado. Sin embargo, ya que un factor de escala es tan sólo 1/z, podemos reutilizar el valor Z de ese sprite! Aunque todavía necesitaremos este factor para determinar los límites del sprite para así poder mantenerlo centrado a medida que se escala.

Glosario

Línea Mala - El chip de gráficos VIC II de la C64, en el primer pixel de cada tile del fondo, toma el control del procesador para obtener más información como los colores. Puesto que quedan menos ciclos para que un programa haga sus cálculos, estas son referidas como líneas malas

Mapa de Altura (Height Map) - Un mapa de altura es un arreglo de valores de alturas. En un motor de polígonos o voxel, este podría ser un arreglo bidimensional (piensa en un paisaje visto desde arriba). Sin embargo, en un motor de carretera, un mapa de altura sólo necesitaría ser de una sola dimensión (piensa en un paisaje visto de costado).

Modo de Color Indexado - Los sistemas más viejos que tenían pocos colores en pantalla a la vez, los muestran generalmente en modos de color indexado. Algunos de los modos de color indexado más habituales son los modos VGA de 256 colores. En estos modos, cada pixel es representado por un byte. Cada byte almacena un valor de índice entre 0 y 255. Cuando se dibuja en pantalla, se busca en la paleta el número de índice para cada pixel. Cada entrada en la paleta puede ser uno de los 262 o 144 posibles colores de VGA. En conclusión, incluso aunque sólo se pueden mostrar 256 colores en pantalla a la vez, el usuario puede escoger cada color de una paleta mucho más grande.

Interpolación Lineal - El proceso de obtener valores intermedios de un conjunto de datos dibujando líneas entre los puntos.

Algoritmo del Pintor - El Algoritmo del Pintor es la técnica de dibujar objetos superponiéndolos del más lejano al más cercano. Este algoritmo se asegura que los objetos más cercanos estén antes que aquellos más lejanos.

Modo de Gráficos Planares - Un modo de Gráficos Planares es aquel en donde una imagen de N bits está hecha de N imágenes de 1 bit combinadas para producir la imagen final. Esto es lo opuesto a la mayoría de los modos gráficos, a veces referidos como sólidos, en donde una imagen de N bits está hecha de valores de pixel de N bits.

Efecto Rasterizado - Un efecto rasterizado es una técnica gráfica que toma ventaja de la naturaleza basada en scanlines de la mayoría de las computadoras.

Factor de Escalado - El recíproco de Z. Este te da la cantidad a la cual escalar un objeto a una distancia Z dada.

Segmento (Carretera) - Estoy usando el término segmento para referirme a una posición en donde debajo, la carretera actúa de una manera, y de forma diferente arriba de la misma. Por ejemplo, el segmento podría dividir una curva hacia la izquierda en la parte inferior de la pantalla de una curva hacia la derecha en la parte superior. A medida que el segmento se dirige hacia el jugador, la carretera parecerá zigzaguear a izquierda y derecha.

Segmento, 3d (Carretera) - Utilizo el término segmento 3d para referirme a una línea horizontal que tiene tanto una distancia Z como una altura Y. A diferencia de un vertex, que podría ser un punto 3d, un segmento tridimensional sería una línea 3d con los puntos extremos izquierdo y derecho del eje X al infinito negativo y positivo.

Voxel - Un pixel 3d. Los motores de Raycast/escenarios con voxel fueron popularizados en el juego Commanche: Maximum Overkill.

Z Map - Una tabla que asocia cada línea de la pantalla con una distancia Z.

La Galería

Cisco Heat

Las colinas en este juego vienen hacia ti como una pared sólida. Las curvas también son bastante exageradas. El motor parece muy flexible y soporta múltiples carreteras simultáneamente, así como también es capaz de mostrar la altura de una carretera en relación con la otra.

Pole Position

Este es el primer juego de carreras pseudo 3d con movimiento suave que recuerdo. No es extremadamente impresionante gráficamente hasta el día de hoy.

Hydra

Este es otro shoot'em up de Atari del tipo Roadblasters. Contiene un efecto de salto muy bueno en donde la perspectiva de la capa de la carretera se voltea, haciendo que los objetos más cercanos caigan de la pantalla. También proyecta muy bien los objetos a varias distancias sobre el suelo.

Outrunners

Esta secuela de Outrun es un claro ejemplo de colinas al estilo montaña rusa en un juego de carreras. Todo es bastante exagerado, y el resultado es uno de los juegos de carreras más deslumbrantemente rápidos y aún fácilmente controlables de todos los tiempos.

Road Rash

En la versión de Road Rash para 32 bits, todo estaba texturizado y las edificaciones fueron inteligentemente dibujadas a continuación de la carretera, dejando a algunas personas con la impresión de que era un juego enteramente poligonal que se ejecutaba a gran velocidad en la 3do. Sin embargo, la forma en la que los objetos azotan las esquinas, las deformaciones de las construcciones, y el hecho de que no puedas regresar parecieran revelar que no es realmente un motor poligonal. Las líneas pronunciadas en el pavimento, sin embargo, dan pista de una suerte de sistema de segmentos proyectados. Los caminos tienen muchos detalles y variedad. El Road Rash para la generación de 16 bits tampoco aflojó, presentando también un motor flexible con una pequeña cantidad de texturas falsas (sin embargo era lento).

Turbo

Este juego precede a Pole Position y también posee colinas y puentes. La desventaja? No hay transiciones de las colinas al puente o a la curva. Utilizaba hardware de escalado de gráficos analógicos.

Spy Hunter II

No sé en qué estaban pensando los creadores de Spy Hunter II. Buena idea, mala ejecución. Los efectos de la carretera lucen muy parecidos a los de Turbo con un poco más de transiciones.

Pitstop II

Esta técnica es tan rápida que en la lenta Commodore 64, la gente era capaz de conseguir un juego de carreras con pantalla dividida.

Enduro

Enduro demuestra el uso del pseudo 3d en la Atari 2600.

Enduro Racer

A no confundirse con Enduro, este fue una especie de juego al estilo Excitebike en 3d. La captura de pantalla muestra la técnica de la colina. Las colinas son bastante pronunciadas, flexibles, pero generalmente no afecta la posición del horizonte, por lo que supongo puntos interpolados.

Lotus

Lotus viene con la perfecta técnica de la colina curva. Un aspecto interesante es que Lotus dibuja la parte superior de la carretera debajo del horizonte y luego rellena el hueco con un color sólido para dar la sensación de una pendiente.

Test Drive II

No estoy seguro exactamente de qué hacer con los gráficos de Test Drive 2. Pese a que claramente no es poligonal, trata de representar una variedad de carreteras de manera realista. El juego es parecido a la serie Need for Speed pero salió varios años antes.

Speed Buggy

Cuando doblas en este juego, además de alterar la perspectiva, la carretera también se desliza un poco a izquierda y derecha.